Werbung
In diesem Artikel wird an einem Beispiel gezeigt, wie man eine Rollenkette für einen konkreten Anwendungsfall dimensioniert. Dabei wird die Vorgehensweise des Kettenherstellers Iwis angewendet, die in seinem Handbuch Kettentechnik beschrieben sind. In den einzelnen Passagen wird jeweils zur passenden Seite in diesem Handbuch oder den Kettenkatalogen verlinkt.
Der Kettentrieb
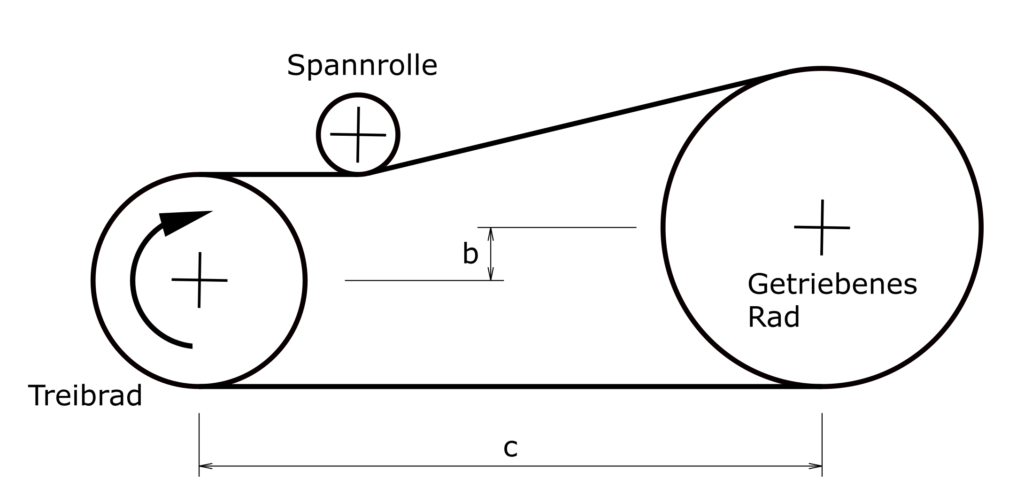
Eine Kette soll in einem gegebenen Bauraum für den Antrieb eines Förderbands zur Beförderung von Stückgut eingesetzt werden. Als Antriebsmotor wird ein Elektromotor eingesetzt, es ist mit leichten Stößen im Betrieb zu rechnen. Das Umfeld des Kettenantriebs ist sauber, so dass im Betrieb keine Verunreinigungen zu erwarten sind. Die folgenden Daten sind gegeben:
| Abstand | a | 1500 mm |
| Abstand | b | 300 mm |
| Antriebsdrehzahl | nAn | 1000 min-1 |
| Abtriebsdrehzahl | nAb | 200 min-1 |
| Abtriebsmoment | MAb | 50 Nm |
| Bauhöhe | h | 400 mm |
Entwurfsrechnung
Der im Folgenden gezeigte Berechnungsvorgang und die verwendeten Parameter sind auf eine Lebensdauer von 15.000 h ausgelegt.
Die benötigte Übersetzung beträgt
\[ i = \frac{n_{An}}{n_{Ab}} = 5 \]
Die Zähnezahl des Antriebsrads wird, um einen möglichst gleichmäßigen Kettenlauf bei kleinem Bauraum zu erreichen, auf
\[ z_1 = 19 \]
festgelegt, womit sich auch die Zähnezahl des angetriebenen Rads ergibt.
\[ z_2 = z_1 \cdot i = 95 \]
Bestimmung der Einflussgrößenfaktoren
Die notwendige Leistung eines Kettentriebs ist von mehren Einflussgrößen abhängig:
- Zähnezahl
- Übersetzungsverhältnis
- Stößen während des Betriebs
- Achsabstand
- Schmierung
- Anzahl der Kettenräder
Diese Einflüsse werden in den nächsten Schritten in Form von Einflussfaktoren bestimmt und zum Abschluss zur Berechnung der erforderlichen Leistung verwendet.
Einfluss der Zähnezahl
Der Einfluss der Zähnezahl des kleinen Rads ist bei 19 Zähnen
\[ f_1 = 1 \]

Einfluss des Übersetzungsverhältnisses
Bei einem Übersetzungsverhältnis von 5:1 beträgt die Einflusszahl
\[ f_2 = 0.92 \]

Betriebscharakteristik (Stöße)
Hier gibt es eine umfangreiche Auflistung bestimmter Antriebs- und Maschinentypen.
Die Stoßzahl Y kann für einen Stückgutförderer auf 2 festgelegt werden. Der Einflussfaktor beträgt 1.37
\[ Y = 2 \]
\[ f_3 = 1.37 \]

Einfluss des Achsabstandsverhältnisses
Für die Bestimmung dieses Werts wird im ersten Schritt der Achabstand
berechnet. Der Achsabstand kann in der hier gewählten Form direkt festgelegt werden, da eine Spannrolle vorgesehen ist. Ansonsten würde sich der Achsabstand u.a. aus der Kettenteilung und Gliederanzahl ergeben.
Für den vorliegenden Fall beträgt der Achsabstand
\[ a = \sqrt{b^2+c^2} = 1530 mm \]
Der Einflussfaktor für das Abstandsverhältnis ist abhängig von der Kettenteilung p. Dies bedeutet, diese muss für die weitere Berechnung angenommen bzw. festgelegt werden.
Da die Bauhöhe der Konstruktion und die Zähnezahl des angetriebenen Rads bereits feststehen, wird die erforderliche Teilung wie folgt geschätzt:
\[ p \approx \frac{h \cdot \pi}{z_2} = 13.22mm \]
Die nächstgelegene Teilung gem. Norm wird gewählt und beträgt
\[ p = 12.7 mm \]
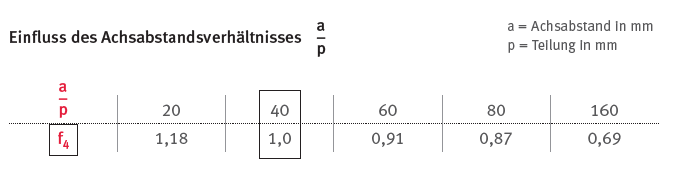
Damit kann der gesuchte Einflussgrößenfaktor für das Achsabstandsverhältnis aus der Tabelle interpoliert werden. Er beträgt
\[ f_4 = 0.79 \]
Einfluss der Schmierung
Für diesen Einflussfaktor muss die Kettengeschwindigkeit berechnet
werden. Sie errechnet sich aus dem Teilkreisdurchmesser und der
Drehzahl.
Der Teilkreisdurchmesser des angetriebenen Rads ist
\[ d_{T2} = \frac{z_2 \cdot p}{\pi} = 384 mm \]
Die Kettengeschwindigkeit beträgt
\[ v = \pi \cdot d_{T2} \cdot n_{Ab} = 4 \frac{m}{s} \]
Hinsichtlich der Schmierung wird auf weitere konstruktive Maßnahmen verzichtet, d.h. es ist damit zu rechnen, dass die Schmierung "mangelhaft, aber ohne Verschmutzungen" ist. Damit ist der Einflussfaktor
\[ f_5 = 2.5 \]
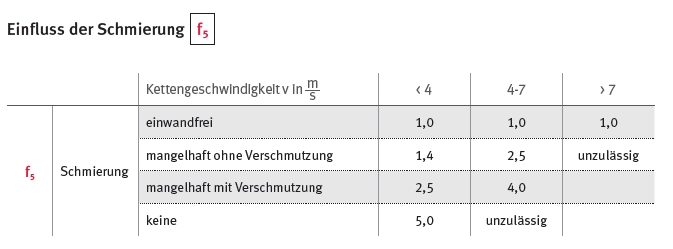
Damit ist zu erkennen, dass der Einfluss der Schmierung auf die erforderliche Kettenleistung erheblich ist.
Anzahl der Kettenräder
Der Einflussfaktor für die Anzahl der Kettenräder beträgt für den vorliegenden Fall
\[ f_6 = 1 \]
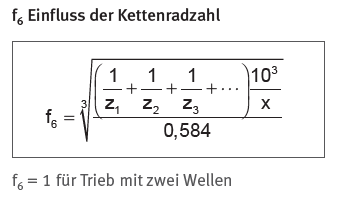
Die Spannrolle wird nicht zu den Kettenrädern hinzugezählt.
Berechnung der Leistung und Auswahl der Kette
Die Antriebsleistung wird zurückgerechnet aus dem Abtriebsmoment und der Abtriebsdrehzahl. Da die Verluste des Triebstrangs als in den Einflussfaktoren ausreichend berücksichtigt angesehen werden, wird hier auf die Einführung eines Wirkungsgrads zwischen Antrieb und Abtrieb verzichtet. Die Antriebsleistung beträgt demnach:
\[ P_0 = 2 \cdot \pi \cdot n_{Ab} \cdot M_{Ab} = 1050 W \]
Die sogenannte Diagrammleistung PD wird nun aus dem vorigen Wert und den Einflussfaktoren ermittelt.
\[ P_D = P_0 \cdot f_1 \cdot f_2 \cdot f_3 \cdot f_4 \cdot f_5 \cdot f_6 \]
\[ P_D = 2574 W \]
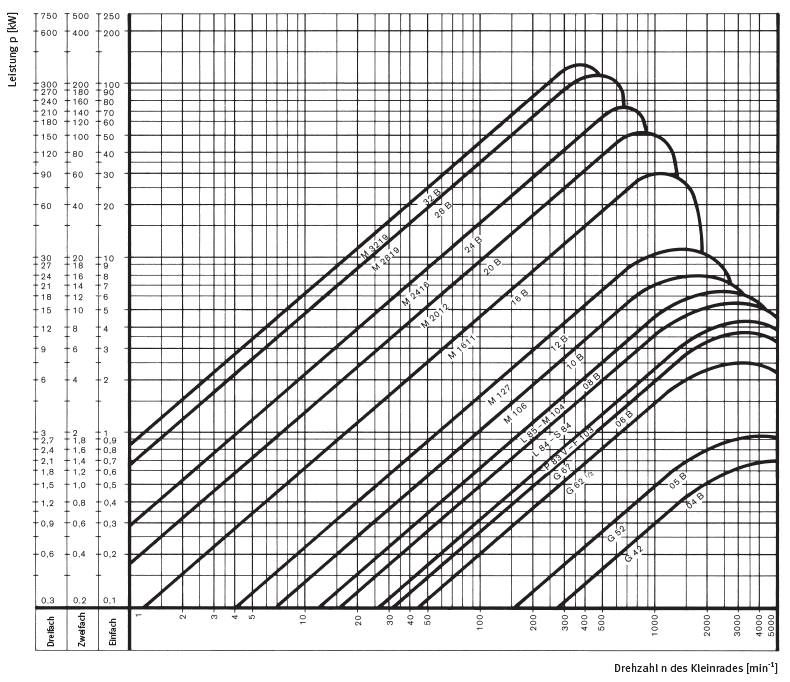
Mit diesem Wert und der Drehzahl des Antriebsrads kann nun aus dem Leistungsdiagramm eine Kette ausgewählt werden. Die Wahl fällt auf eine Einfach-Kette Typ 08B-1.
Überprüfung der gewählten Kette
Nun werden Informationen zu der gewählten Kette 08B-1 aus dem Rollenkettenkatalog benötigt.
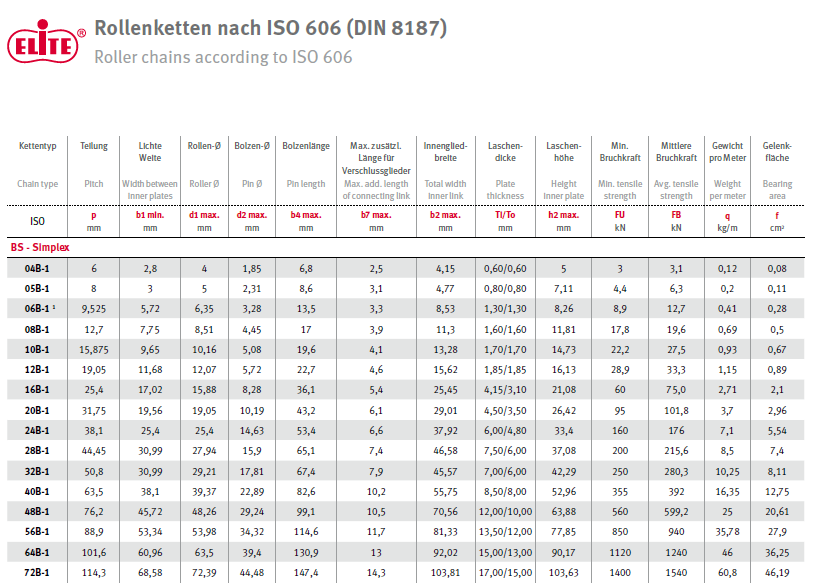
Die Kette wiegt
\[ q = 0.69 \frac{kg}{m} \]
Die Fliehkraft beträgt
\[ F_F = q \cdot v^2 = 11 N \]
Die Kettenzugkraft beträgt
\[ F_Z = \frac{P_D}{v} = 640 N \]
Die Gesamtkettenkraft beträgt
\[ F_G = F_F + F_Z = 651 N \]
Sicherheit gegen Bruch
Die mittlere Bruchkraft der Kette 08B-1 ist gemäß Katalogangabe
\[ F_B = 19.6 kN \]
Die statische Sicherheit gegen Bruch beträgt daher
\[ \gamma_{st} = \frac{F_B}{F_G} = 30\]
Zur Bestimmung der dynamischen Sicherheit wird der Stoßfaktor Y hinzugezogen
\[ \gamma_{d} = \frac{F_B}{F_G \cdot Y} = 15\]
Beide Werte sind ausreichend groß.
Überprüfung der Gelenkflächenpressung
Die Gelenkfläche der Kette 08B-1 beträgt gem. Kettenkatalog
\[ f = 0.5 cm^2 \]
Damit beträgt die rechnerische Flächenpressung
\[ p_r = \frac{F_G}{f} = 1302 \frac{N}{cm^2} \]
Dieser Wert wird als nächstes mit der zulässigen Gelenkflächenpressung verglichen. Die zulässige Gelenkflächenpressung berechnet sich aus dem Richtwert pv, dem Reibwegfaktor λ und den beiden Einflussfaktoren für Schmierung f5 und Kettenradanzahl f6. Die beiden bislang noch nicht bekannten Größen werden wieder aus entsprechenden Tabellen entnommen.
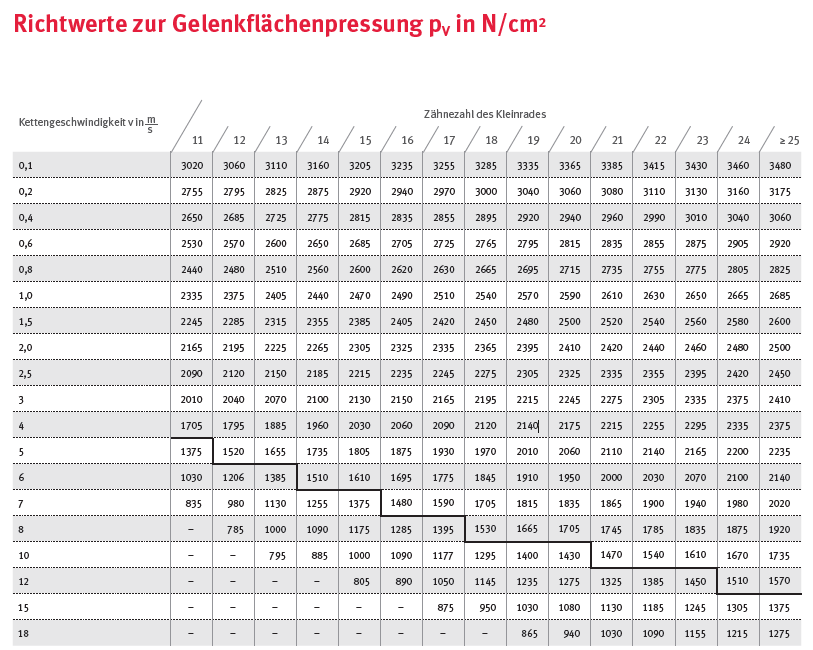
Für den vorliegenden Fall beträgt er
\[ p_v = 2140 \frac{N}{cm^2} \]
Der Reibwegfaktor muss aus der Tabelle interpoliert werden.
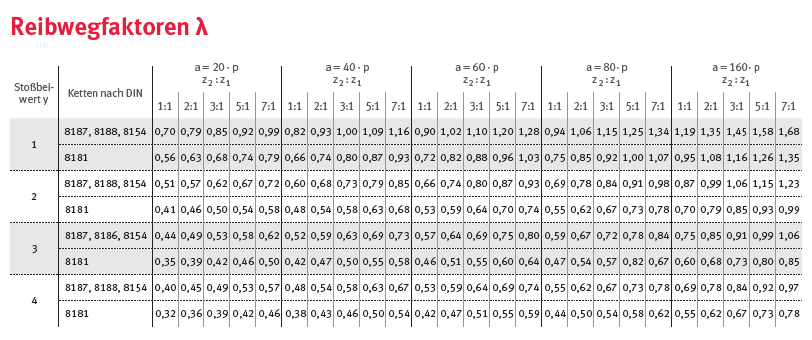
Es wird folgender Wert ermittelt
\[ \lambda = 1.03 \]
Damit kann die zulässige Gelenkflächenpressung nun ermittelt werden. Sie beträgt
\[ p_{zul} = \frac{p_v \cdot \lambda}{f_5 \ cdot f_6} = 882 N\]
Dieser Wert liegt unter der berechneten Gelenkflächenpressung. Die ausgewählte Kette 08B-1 ist also unterdimensioniert!
Iteration mit neuer Kette
Es wird nun aus dem Kettenkatalog eine Bauart mit größerer Gelenkfläche gewählt. Die Wahl fällt auf die Kette 08B-2.
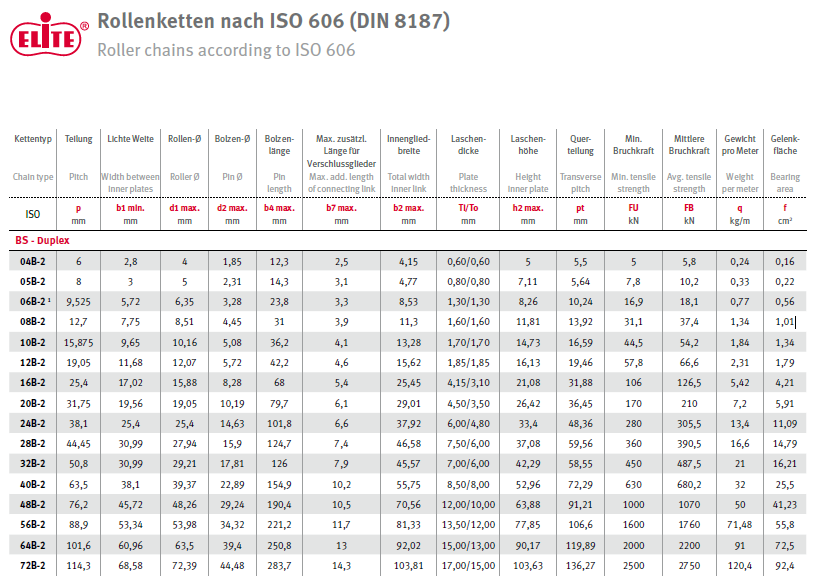
Die Kette wiegt
\[ q = 1.34 \frac{kg}{m} \]
Die Fliehkraft beträgt
\[ F_F = q \cdot v^2 = 21 N \]
Die Kettenzugkraft beträgt
\[ F_Z = \frac{P_D}{v} = 640 N \]
Die Gesamtkettenkraft beträgt
\[ F_G = F_F + F_Z = 661 N \]
Sicherheit gegen Bruch
Die mittlere Bruchkraft der Kette 08B-1 ist gemäß Katalogangabe
\[ F_B = 37.4 kN \]
Die statische Sicherheit gegen Bruch beträgt daher
\[ \gamma_{st} = \frac{F_B}{F_G} = 56\]
Zur Bestimmung der dynamischen Sicherheit wird der Stoßfaktor Y hinzugezogen
\[ \gamma_{d} = \frac{F_B}{F_G \cdot Y} = 28\]
Beide Werte sind erwartungsgemäß ausreichend groß.
Überprüfung der Gelenkflächenpressung
Die Gelenkfläche der Kette 08B-2 beträgt gem. Kettenkatalog
\[ f = 1.01 cm^2 \]
Damit beträgt die rechnerische Flächenpressung
\[ p_r = \frac{F_G}{f} = 654 \frac{N}{cm^2} \]
Der Wert für die zulässige Gelenkflächenpressung ist unverändert. Der Wert wird nun nicht mehr überschritten
\[ p_r = 654 \frac{N}{cm^2} < p_{zul} = 882 \frac{N}{cm^2}\]
Die Kette ist ausreichend dimensioniert.
Bestimmung der Kettenlänge
Die Kettenlänge wird in diesem Beispiel mit dem bereits konstruktiv gegebenen Achsabstand berechnet. Die Gliederanzahl berechnet sich aus
\[ X = \frac{2a}{p} + \frac{z_1 + z_2}{2} + \left( \frac{z_2 - z_1}{2 \pi} \right)^2 \cdot \frac{p}{a} \]
Auf die nächsthöhere gerade Zahl aufgerundet ergibt dies
\[ X = 300 \]
Damit ist die erforderliche Kette bestimmt. Für die finale konstruktive Festlegung empfiehlt es sich, den jeweiligen Kettenlieferanten für eine Detailberechnung hinzuzuziehen.
Werbung




