Werbung
In dieser Übung werden die Lagerreaktionen eines auf drei Stützen gelagerten, symmetrischen Mehrfeldträgers berechnet. Hier gibt es einen Onlinerechner zur Berechnung von asymmetrischen Mehrfeldträgern.
Aufgabe
Ein durchgehender Träger auf einem Festlager und zwei Loslagern (Mehrfeldträger) mit der symmetrischen Stützenweite l wird durch eine Streckenlast q0 belastet. Wie groß sind die Lagerreaktionen?
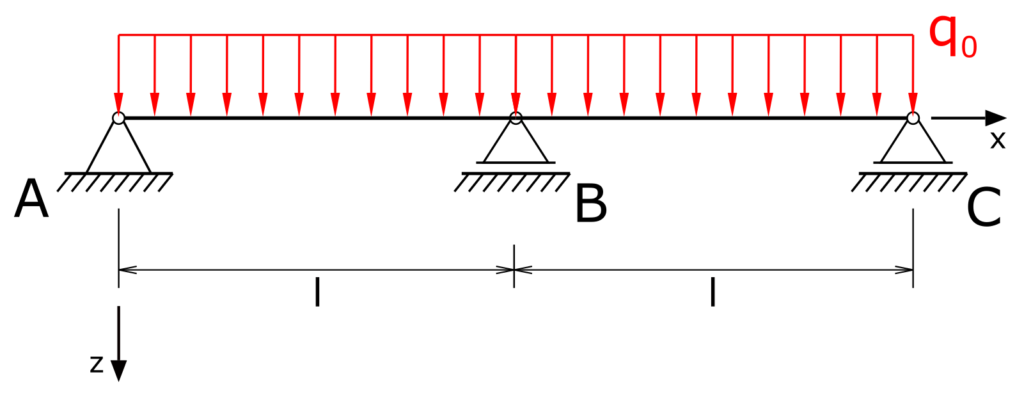
Lösung
Im ersten Schritt werden die Gleichungen für die Lagerreaktionen ermittelt. Für die spätere Ermittlung der Schnittgrößen wird der Träger in zwei Bereiche eingeteilt. In den nachfolgenden Gleichungen werden die Horizontalkräfte nicht weiter betrachtet, da sie offensichtlich Null sind. Linksdrehende Momente sind positiv.
Ermittlung der Lagerreaktionen
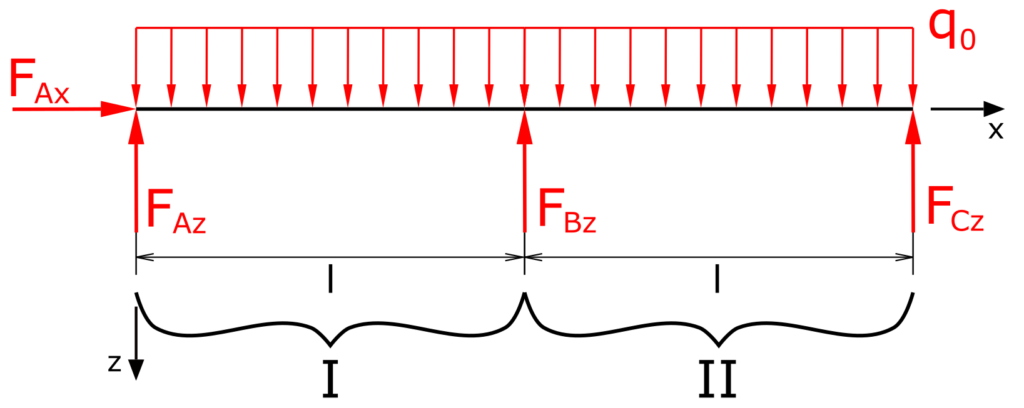
Die Summe der Kräfte in z-Richtung liefert
\[ \tag{1} \sum F_z = 0 = -F_{Az} - F_{Bz} - F_{Cz} + \int_0^{2l}{q_0dx} \]
\[ \tag{2} 0 = -F_{Az} - F_{Bz} - F_{Cz} + 2 \cdot q_0 \cdot l \]
Die Summe der der Momente um A
\[ \tag{3} \sum M(A) = 0 = F_{Bz} \cdot l + 2 \cdot F_{Cz} \cdot l - \int_0^{2l}{q_0xdx} \]
\[ \tag{4} 0 = F_{Bz} \cdot l + 2 \cdot F_{Cz} \cdot l - 2 \cdot q_0 \cdot l^2 \]
Damit liegt nun ein Gleichungssystem mit 2 Gleichungen, aber 3 Unbekannten vor. Als nächster Schritt werden die Schnittgrößen in den beiden Bereichen I und II ermittelt. Um die Funktion der Streckenlast von 0 bis x integrieren zu können, wird sie als Funktion der Hilfskoordinate ξ formuliert. Normalkräfte werden mit N bezeichnet, Querkräfte mit Q und Biegemomente mit Mb.
Ermittlung der Schnittgrößen
Bereich I
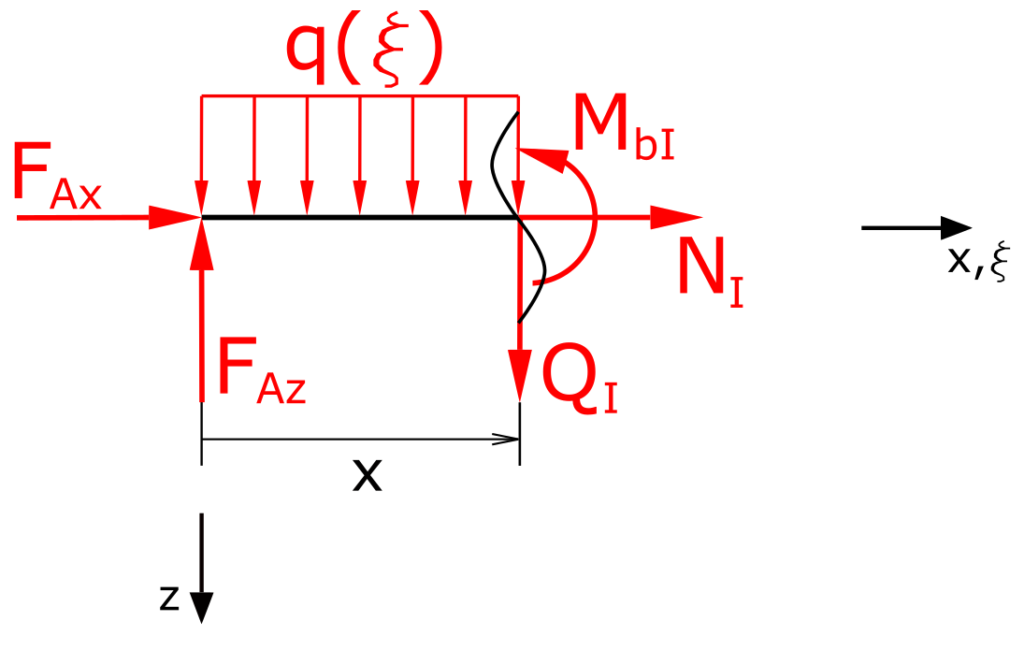
Die Summe der Kräfte in z-Richtung liefert
\[ \tag{5} \sum F_z = 0 = -F_{Az} + Q_I + \int_0^{x}{q_0d \xi} \]
\[ \tag{6} 0 = -F_{Az} + Q_I + q_0 \cdot x \]
Die Summe der der Momente um x
\[ \tag{7} \sum M(x) = 0 = \int_0^{x}{q_0 \xi d \xi} - F_{Az} \cdot x + M_{bI} \]
\[ \tag{8} 0 = \frac{1}{2} q_0 x^2 - F_{Az} \cdot x + M_{bI} \]
Bereich II
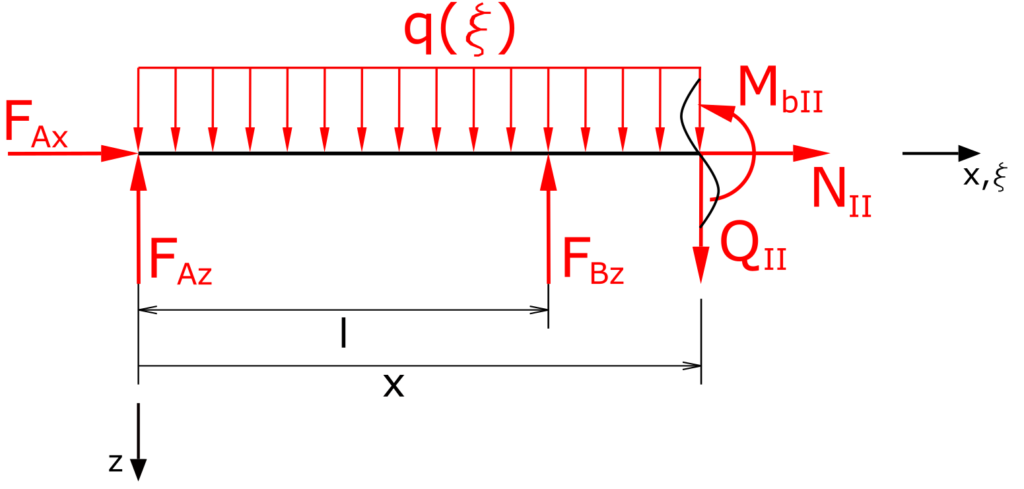
Die Summe der Kräfte in z-Richtung liefert
\[ \tag{9} \sum F_z = 0 = -F_{Az} -F_{Bz}+ Q_{II} + \int_0^{x}{q_0d \xi} \]
\[ \tag{10} 0 = -F_{Az} -F_{Bz}+ Q_{II} + q_0 x \]
Die Summe der der Momente um x
\[ \tag{11} \sum M(x) = 0 = \int_0^{x}{q_0 \xi d \xi} - F_{Az} \cdot x - F_{Az} \cdot (x-l) + M_{bII} \]
\[ \tag{12} 0 = \frac{1}{2} q_0 x^2 - F_{Az} \cdot x - F_{Bz} \cdot (x-l) + M_{bII} \]
Als nächstes werden die Funktionen der Biegelinien berechnet.
Biegelinien
Die Funktion der Biegelinie wird als w bezeichnet, bzw. die erste Ableitung als w' und die zweite Ableitung als w''. Der Elastizitätsmodul ist E und das Flächenträgheitsmoment I.
Bereich I
\[ \tag{13} M_{bI} = -\frac{{q_0} {{x}^{2}}-2 {F_{\mathit{Az}}} x}{2} \]
\[ \tag{14} w''_I = - \frac{1}{E \cdot I} M_{bI} \]
\[ \tag{15} w''_I = \frac{{q_0} {{x}^{2}}-2 {F_{\mathit{Az}}} x}{2 E I} \]
\[ \tag{16} w'_I = \frac{\frac{{q_0} {{x}^{3}}}{3}-{F_{\mathit{Az}}} {{x}^{2}}}{2 E I}+\mathit{ c_1} \]
\[ \tag{17} w_I = \frac{\frac{{q_0} {{x}^{4}}}{12}-\frac{{F_{\mathit{Az}}} {{x}^{3}}}{3}}{2 E I}+\mathit{ c_1} x+\mathit{ c_2} \]
Bereich II
\[ \tag{18} M_{bII} = -\frac{{q_o} {{x}^{2}}+\left( -2 {F_{\mathit{Bz}}}-2 {F_{\mathit{Az}}}\right) x+2 {F_{\mathit{Bz}}} l}{2}\]
\[ \tag{19} w''_{II} = - \frac{1}{E \cdot I} M_{bII} \]
\[ \tag{20} w''_{II} = \frac{{q_o} {{x}^{2}}+\left( -2 {F_{\mathit{Bz}}}-2 {F_{\mathit{Az}}}\right) x+2 {F_{\mathit{Bz}}} l}{2 E I} \]
\[ \tag{21} w'_{II} = \frac{\frac{{q_o} {{x}^{3}}}{3}+\frac{\left( -2 {F_{\mathit{Bz}}}-2 {F_{\mathit{Az}}}\right) {{x}^{2}}}{2}+2 {F_{\mathit{Bz}}} l x}{2 E I}+\mathit{ c_3} \]
\[ \tag{22} w_{II} = \frac{\frac{{q_o} {{x}^{4}}}{12}+\frac{\left( -2 {F_{\mathit{Bz}}}-2 {F_{\mathit{Az}}}\right) {{x}^{3}}}{6}+{F_{\mathit{Bz}}} l\, {{x}^{2}}}{2 E I}+\mathit{ c_3} x+\mathit{ c_4} \]
Die Integrationskonstanten werden über die Rand- und Nebenbedingungen ermittelt.
Rand- und Nebenbedingungen
Die Durchbiegung an der Stelle x = 0 ist gleich Null.
\[ \tag{23} 0=\mathit{c_2} \]
Die Durchbiegung an der Stelle x = l ist gleich Null. Diese Bedingung kann für beide Biegelinien genutzt werden.
\[ \tag{24} \frac{\frac{{{l}^{4}}\, {q_0}}{12}-\frac{{F_{\mathit{Az}}} {{l}^{3}}}{3}}{2 E I}+\mathit{c_1} l = 0\]
\[ \tag{25} \frac{\frac{{{l}^{4}}\, {q_o}}{12}+{F_{\mathit{Bz}}} {{l}^{3}}+\frac{\left( -2 {F_{\mathit{Bz}}}-2 {F_{\mathit{Az}}}\right) {{l}^{3}}}{6}}{2 E I}+\mathit{ c_3} l+\mathit{ c_4}=0\]
Die Durchbiegung an der Stelle x = 2l ist gleich Null.
\[ \tag{26} \frac{\frac{4 {{l}^{4}}\, {q_o}}{3}+4 {F_{\mathit{Bz}}} {{l}^{3}}+\frac{4 \left( -2 {F_{\mathit{Bz}}}-2 {F_{\mathit{Az}}}\right) {{l}^{3}}}{3}}{2 E I}+2 \mathit{ c_3} l+\mathit{ c_4} \]
Beide Biegelinien haben an der Stelle x = l den gleichen Anstieg.
\[ \tag{27} \frac{\frac{{{l}^{3}}\, {q_0}}{3}-{F_{\mathit{Az}}} {{l}^{2}}}{2 E I}+\mathit{ c_1} = \frac{\frac{{{l}^{3}}\, {q_o}}{3}+2 {F_{\mathit{Bz}}} {{l}^{2}}+\frac{\left( -2 {F_{\mathit{Bz}}}-2 {F_{\mathit{Az}}}\right) {{l}^{2}}}{2}}{2 E I}+\mathit{ c_3} \]
Damit liegen nun ausreichend Gleichungen vor, um die Unbekannten auflösen zu können.
\[ \tag{28} \mathit{ c_1}=\frac{11 {{l}^{3}}\, {q_o}-9 {{l}^{3}}\, {q_0}}{96 E I} \]
\[ \tag{29} c_2 = 0 \]
\[ \tag{30} \mathit{ c_3}=\frac{61 {{l}^{3}}\, {q_o}-119 {{l}^{3}}\, {q_0}}{96 E I} \]
\[ \tag{31} \mathit{ c_4}=-\frac{5 {{l}^{4}}\, {q_o}-15 {{l}^{4}}\, {q_0}}{48 E I} \]
\[ \tag{32} {F_{\mathit{Az}}}=\frac{11 l\, {q_o}-5 l\, {q_0}}{16} \]
\[ \tag{33} {F_{\mathit{Bz}}}=-\frac{11 l\, {q_o}-21 l\, {q_0}}{8} \]
\[ \tag{34} {F_{\mathit{Cz}}}=\frac{11 l\, {q_o}-5 l\, {q_0}}{16} \]
Und der Vollständigkeit halber
\[ \tag{35} F_{Ax} = 0 \]
Werbung




