Start » Übungen » Technische Mechanik I » Resultierende Kraft und Moment berechnen, dreidimensional

Resultierende Kraft und Moment berechnen, dreidimensional

Werbung

In dieser Übung wird gezeigt, wie man ein resultierendes Moment dreidimensional berechnen kann, indem man die Kreuzprodukte aus Ortsvektoren und Kraftvektoren bildet.

Aufgabe

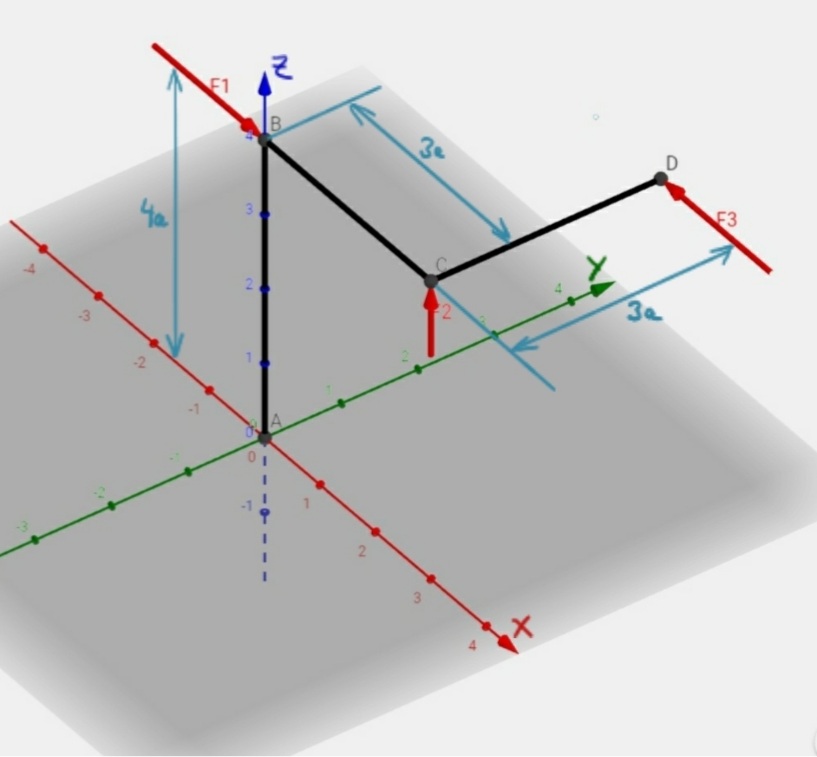
An einem Rahmen greifen die Kräfte F1, F2 und F3 wie abgebildet an. Die angreifenden Kräfte sind in Punkt A und Punkt B zusammenzufassen. Wie groß sind jeweils die resultierende Kraft und das resultierende Moment?

geg.: F1 = 2F, F2 = F, F3 = 2F, a

Rahmen mit angreifenden Kräften, dreidimensional
Rahmen mit angreifenden Kräften, dreidimensional

Lösung

Resultierende Kraft und Moment berechnen, dreidimensional - Technische Mechanik 1, Übung 10
Lösungsvideo zu Übung 10
\[ \newcommand{\myvec}[1]{{\begin{pmatrix}#1\end{pmatrix}}} \]

Die Kraftvektoren lauten

\[\tag{1} \vec{F_1} = \myvec{2F\\0\\0} , \vec{F_2} = \myvec{0\\0\\F} , \vec{F_3} = \myvec{-2F\\0\\0}\]
\[ \newcommand{\myvec}[1]{{\begin{pmatrix}#1\end{pmatrix}}} \]

Die Ortsvektoren müssen für die beiden zu betrachtenden Fällen separat definiert werden. Für das resultierende Moment in Punkt A sind es

\[\tag{2} \vec{r_{1A}} = \myvec{0\\0\\4a} , \vec{r_{2A}} = \myvec{3a\\0\\4a} , \vec{r_{3A}} = \myvec{3a\\3a\\4a}\]
\[ \newcommand{\myvec}[1]{{\begin{pmatrix}#1\end{pmatrix}}} \]

Für das resultierende Moment in Punkt B lauten sie

\[\tag{3} \vec{r_{1B}} = \myvec{0\\0\\0} , \vec{r_{2B}} = \myvec{3a\\0\\0} , \vec{r_{3B}} = \myvec{3a\\3a\\0}\]
\[ \newcommand{\myvec}[1]{{\begin{pmatrix}#1\end{pmatrix}}} \]

Die resultierende Kraft ist, unabhängig ob sie für A oder B berechnet wird, gleich groß:

\[\tag{4} \sum \vec{F_A} = \sum \vec{F_B} = \vec{F_1} + \vec{F_2} + \vec{F_3} \]

\[\tag{5} \sum \vec{F} = \myvec{2F\\0\\0} + \myvec{0\\0\\F} + \myvec{-2F\\0\\0} \]

\[\tag{6} \sum \vec{F} = \myvec{0\\0\\F} \]

\[ \require{cancel} \] \[ \newcommand{\myvec}[1]{{\begin{pmatrix}#1\end{pmatrix}}} \]

Das resultierende Moment in Punkt A ergibt sich aus der Summe der Kreuzprodukte von Kraft- und Ortsvektor, bezogen auf A. Die Vorgehensweise zur Berechnung des Kreuzprodukts wird im o.a. Video beschrieben. Dort wird die Sarrus-Regel angewendet.

\[\tag{7} \sum \vec{M_A} = \vec{r_{1A}} \times \vec{F_1} + \vec{r_{2A}} \times \vec{F_2} + \vec{r_{3A}} \times \vec{F_3} \]

\[\tag{8} \sum \vec{M_A} = \myvec{0\\0\\4a} \times \myvec{2F\\0\\0} + \myvec{3a\\0\\4a} \times \myvec{0\\0\\F} + \myvec{3a\\3a\\4a} \times \myvec{-2F\\0\\0} \]

\[\tag{9} \sum \vec{M_A} = \myvec{0\\-3Fa\\6Fa} \]

\[ \require{cancel} \] \[ \newcommand{\myvec}[1]{{\begin{pmatrix}#1\end{pmatrix}}} \]

Für das resultierende Moment in Punkt B lautet die Gleichung

\[\tag{10} \sum \vec{M_B} = \vec{r_{1B}} \times \vec{F_1} + \vec{r_{2B}} \times \vec{F_2} + \vec{r_{3B}} \times \vec{F_3} \]

\[\tag{11} \sum \vec{M_B} = \myvec{0\\0\\0} \times \myvec{2F\\0\\0} + \myvec{3a\\0\\0} \times \myvec{0\\0\\F} + \myvec{3a\\3a\\0} \times \myvec{-2F\\0\\0} \]

\[\tag{12} \sum \vec{M_B} = \myvec{0\\-3Fa\\6Fa} \]

Dass diese beiden Momente in diesem Fall gleich groß sind, ist der geometrischen Anordnung in dieser Aufgabe geschuldet, d.h. es ist eher wahrscheinlich, dass die Betrachtung unterschiedlicher Punkte auch zu unterschiedlichen Momentenvektoren führt.

Weitere Übungen zum Thema resultierende Momente gibt es hier.

Werbung