Werbung
In dieser Übung wird eine statische Betrachtung der Kräfte und Momente an einem Fahrrad-Triebstrang durchgeführt.
Aufgabe
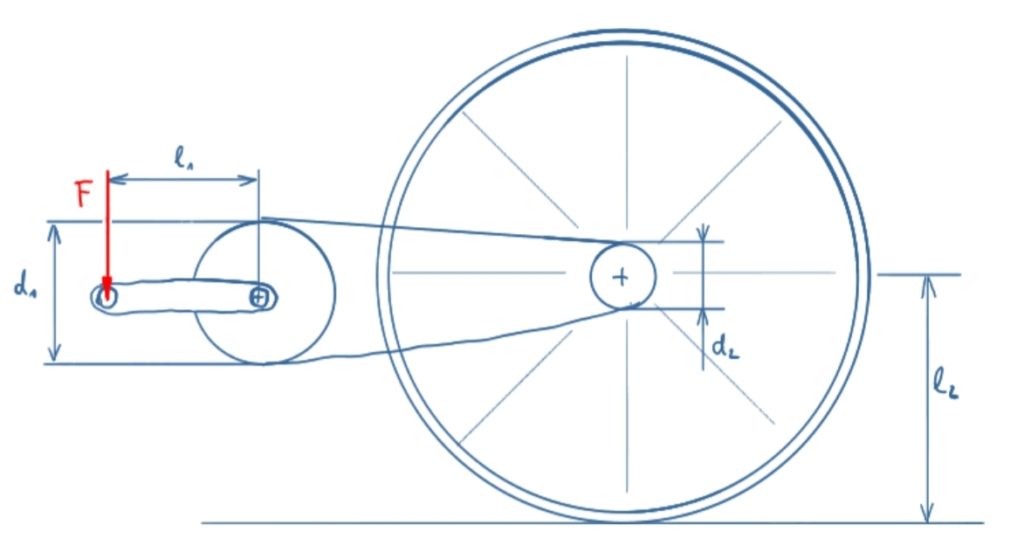
An einer Tretkurbel eines Fahrrads wirkt die Kraft F. Zu berechnen sind
a) das Moment an der Tretkurbelwelle
b) die Zugkraft in der Kette
c) das Moment am Hinterrad
d) die Vortriebskraft des Fahrrads
Lösung
Lösungsskizze
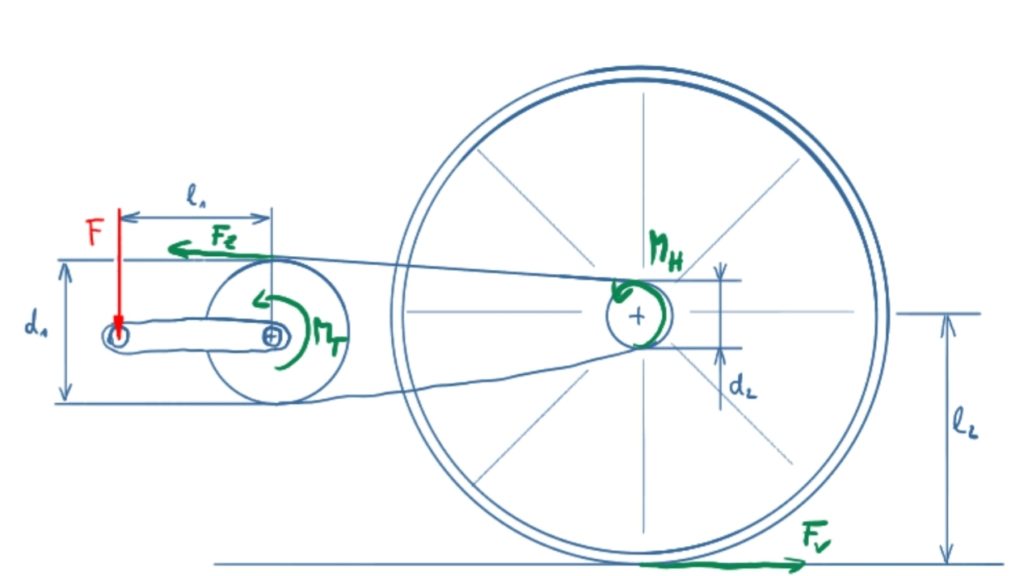
Das Drehmoment an der Tretkurbel beträgt
\[\tag{1} M_T = F \cdot l_1 \]
Die Zugkraft in der Kette ergibt sich aus
\[\tag{2} F_Z = \frac{M_T}{\frac{d_1}{2}} = \frac{2 M_T}{d_1} = \frac{2 F l_1}{d_1} \]
Das Drehmoment am Hinterrad beträgt
\[\tag{3} M_H = F_Z \cdot \frac{d_2}{2} = \frac{\bcancel{2} F l_1}{d_1} \cdot \frac{d_2}{\bcancel{2}} = F l_1 \cdot \frac{d_2}{d_1} \]
Die Vortriebskraft am Hinterrad beträgt
\[\tag{4} F_V = \frac{M_H}{l_2} = F \cdot \frac{l_1}{l_2} \cdot \frac{d_2}{d_1} \]
Soviel zur statischen Betrachtung der Kräfte an einer Fahrrad-Tretkurbel. Eine ähnliche Aufgabe gibt es zum Kurbeltrieb einer Dampfmaschine mit Kreuzkopflagerung.
Werbung




