Werbung
Aufgabe
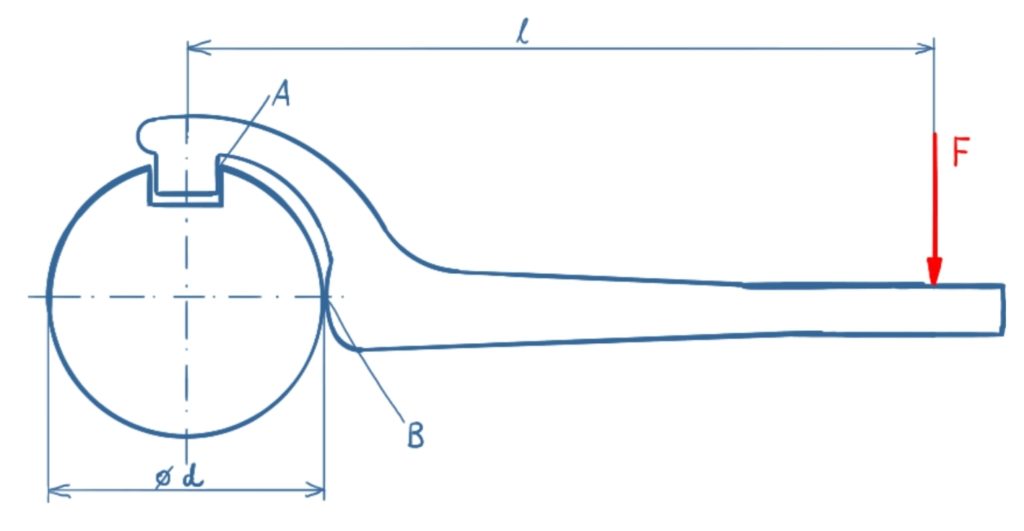
An einer feststehenden Welle wird ein Hakenschlüssel angesetzt. Welche Reaktionskräfte entstehen in A und B unter der Annahme, dass der Kontakt in B reibungsfrei ist?
Lösung
Schriftlicher Lösungsweg
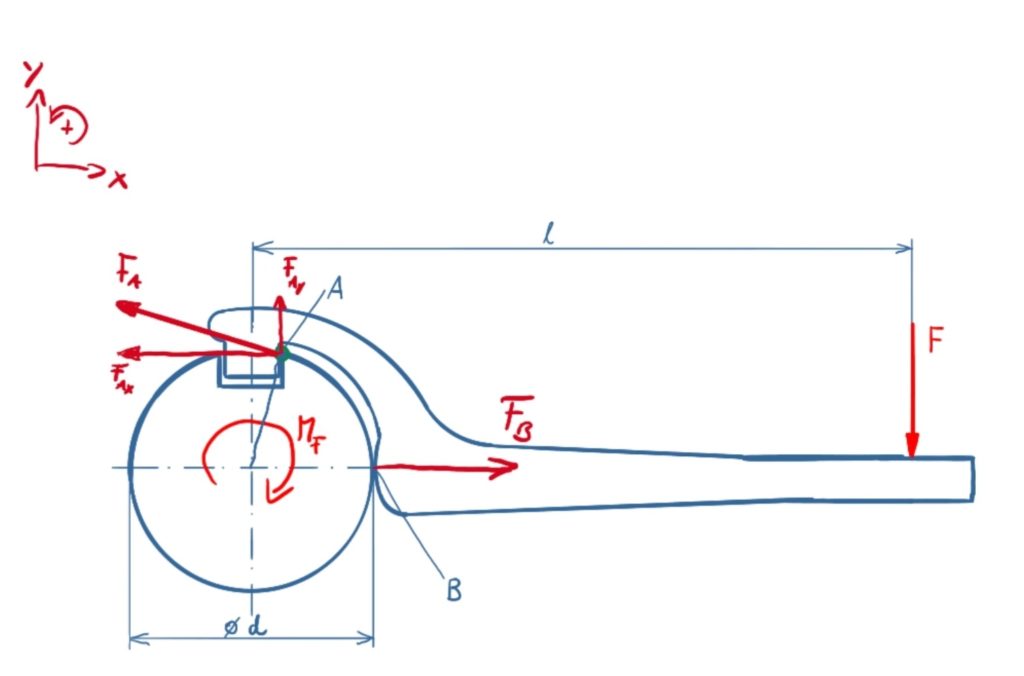
In der Lösungsskizze sind die Reaktionskräfte an der Welle eingetragen. Die Berührung des Hakenschlüssels mit der Welle erfolgt punktförmig in A, bzw. an einer räumlichen Welle würde ein Linienkontakt entstehen.
Das Kräftegleichgewicht in x-Richtung ist
\[\tag{1} \sum F_x = 0 = F_B - F_{Ax} \]
\[\tag{2} F_{Ax} = F_B \]
Das Kräftegleichgewicht in y-Richtung ist
\[\tag{3} \sum F_y = 0 = F_{Ay} - F \]
\[\tag{4} F_{Ay} = F \]
Das Momentengleichgewicht wird um die Drehachse der Welle aufgestellt. Das durch die Kraft F aufgebrachte Moment wird als MF bezeichnet, so dass das Momentengleichgewicht lautet
\[\tag{5} \sum M = 0 = - M_F + F_A \cdot \frac{d}{2} \]
\[\tag{6} F_A \cdot \frac{d}{2} = F \cdot l \]
\[\tag{7} F_A = \frac{2 \cdot F \cdot l}{d} \]
Die noch unbekannten Horizontalkräfte werden über den Satz des Pythagoras berechnet:
\[\tag{8} F_A^2 = F_{Ax}^2 + F_{Ay}^2 \]
\[\tag{9} \left( \frac{2 \cdot F \cdot l}{d} \right)^2 = F_{Ax}^2 + F^2 \]
\[\tag{10} F_{Ax} = \sqrt{\left( \frac{2 \cdot F \cdot l}{d} \right)^2 - F^2} \]
Hier gibt es weitere interessante Aufgaben zum Thema Bestimmung von Reaktionskräften.
Werbung




