Werbung
Diese Übung behandelt folgende Fragen:
- Wie ermittelt man die Beanspruchungsgrößen eines Trägers?
- Wie stellt man den Verlauf der inneren Kräfte eines Trägers dar?
- Wie berechnet man das Biegemoment eines Trägers?
- Wie berechnet man Querkraft und Normalkraft eines Trägers?
Aufgabe
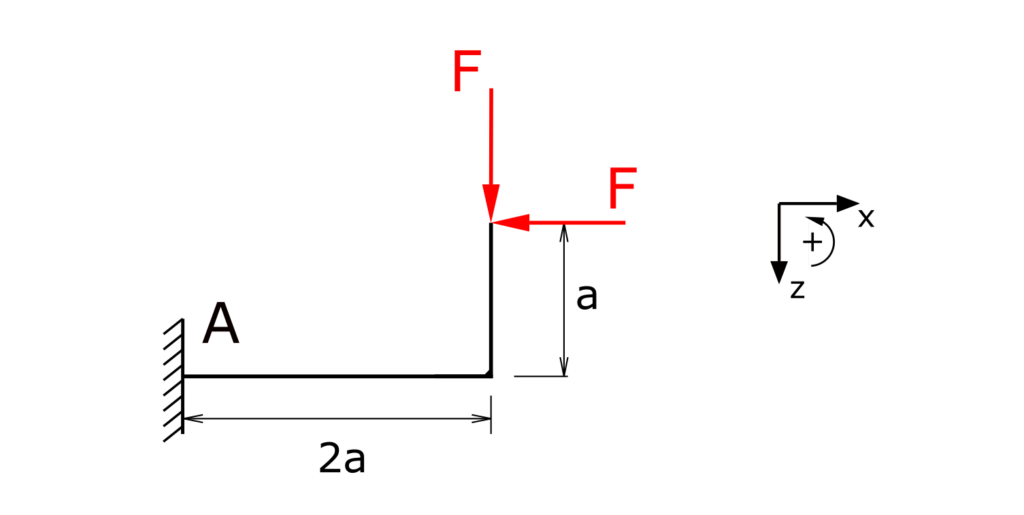
Ein abgewinkelter Träger ist einseitig fest eingespannt und wird am äußeren Ende durch die Kraft F in zwei unterschiedlichen Richtungen belastet. Ermitteln Sie die Beanspruchungsgrößen des Trägers und stellen Sie diese grafisch dar!
Lösung
Zur Lösung der Aufgabe wird der Träger im ersten Schritt in zwei Bereiche eingeteilt, da sich durch die abgewinkelte Form in Verbindung mit den zwei Kräften unterschiedliche Funktionen für den Momentenverlauf ergeben.
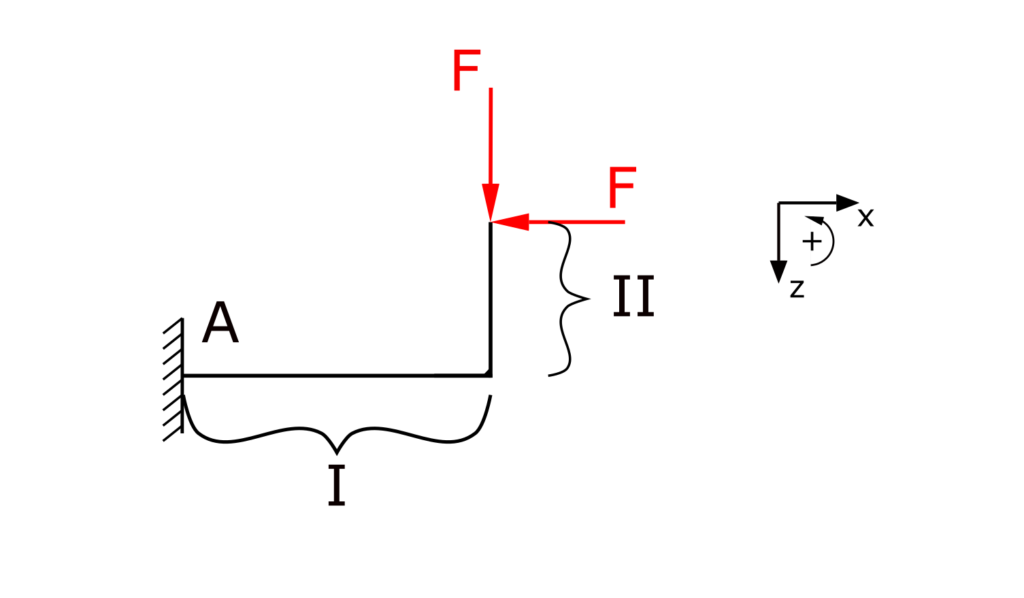
Die Bereiche werden mit I und II bezeichnet.
Die im Folgenden verwendeten Bezeichnungen Fx und Fz stehen in den beiden unterschiedlichen Bereichen jeweils einmal für die Normalkraft bzw. Querkraft, was aus der abgewinkelten Form des Trägers resultiert. (Damit sind die Richtungen x- und z gemeint, die Kräfte werden natürlich eindeutig bezeichnet.) Häufig werden für Normalkraft und Querkraft die Variablen N und Q verwendet. Das Biegemoment wird als Mb bezeichnet.
Die freigeschnittenen Bereiche I und II werden hier so gewählt, dass eine Berechnung der Lagerreaktionen in der festen Einspannung überflüssig ist.
Bereich I
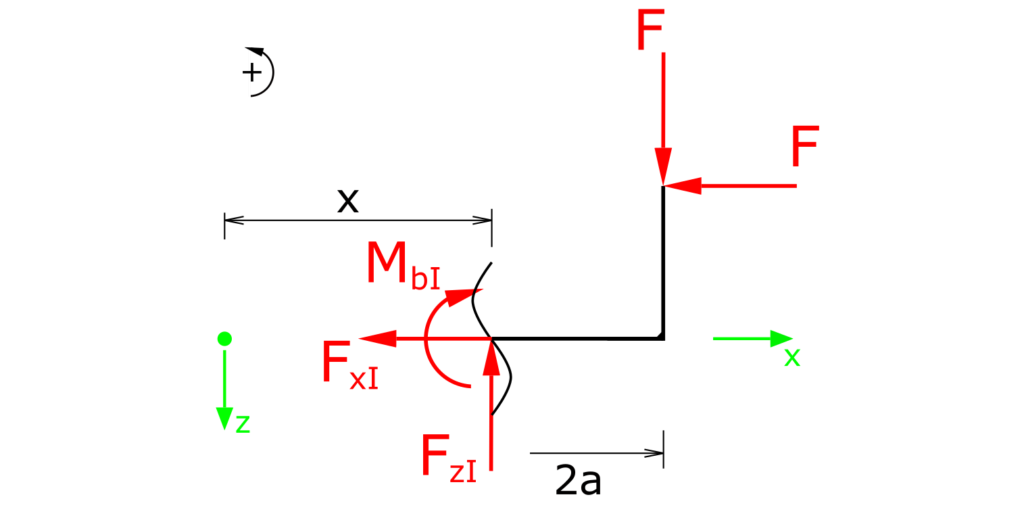
Aufstellen der Gleichgewichtsbedingungen für Kräfte in x-und z-Richtung sowie für die Momente im Bereich I:
\[ \tag{1} \sum F_x = 0 = -F_{xI} - F\]
\[ \tag{2} \sum F_z = 0 = F_{zI} - F\]
\[ \tag{3} \sum M_b(x) = 0 = - M_{bI} - F \cdot (2a - x) + F \cdot a \]
Die beiden Kräfte in x- und z-Richtung sind über den gesamten Bereich I konstant. Das Biegemoment im Bereich I ist eine Funktion von x.
\[ \tag{4} F_{xI} = - F\]
\[ \tag{5} F_{zI} = F\]
\[ \tag{6} M_{bI} = F \cdot (x-a) \]
Bereich II
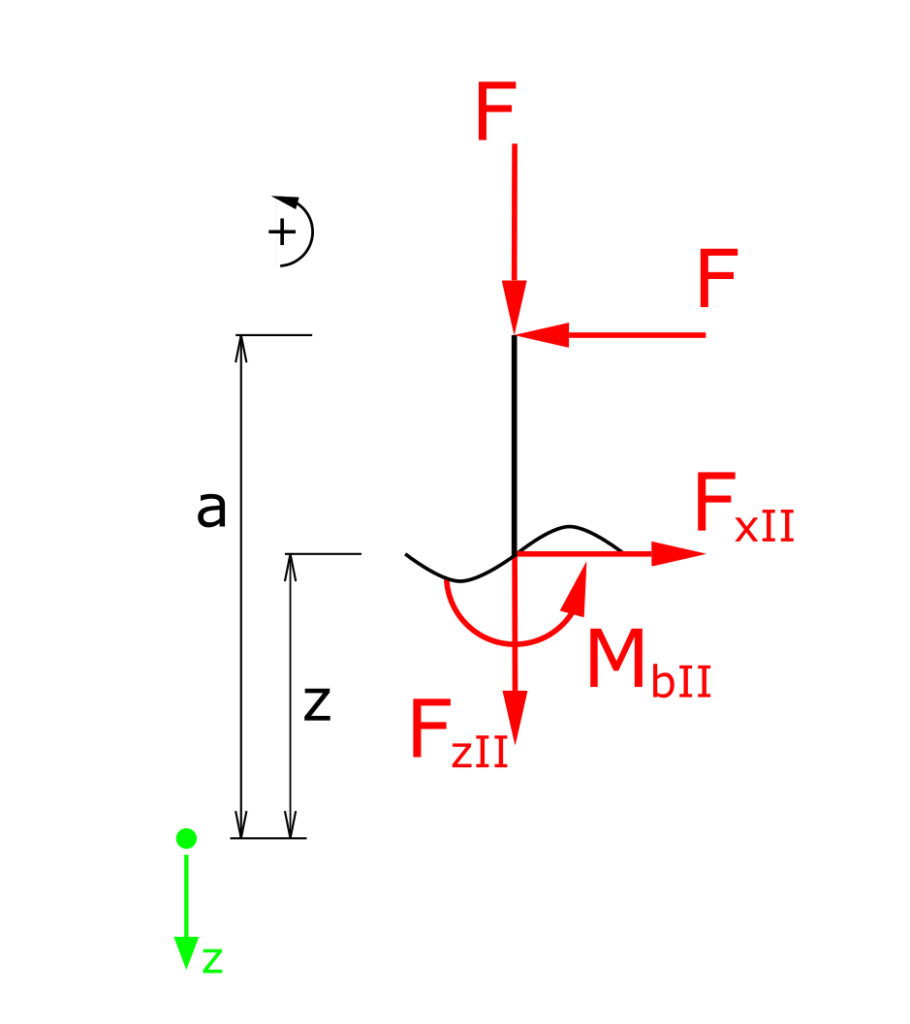
Aufstellen der Gleichgewichtsbedingungen für Kräfte in x-und z-Richtung sowie für die Momente im Bereich II:
\[ \tag{7} \sum F_x = 0 = F_{xII} - F\]
\[ \tag{8} \sum F_z = 0 = -F_{zII} - F\]
\[ \tag{9} \sum M_b(x) = 0 = M_{bII} + F \cdot (a - z) \]
Die beiden Kräfte in x- und z-Richtung sind über den gesamten Bereich II konstant. Das Biegemoment im Bereich II ist eine Funktion von z.
\[ \tag{10} F_{xII} = F\]
\[ \tag{11} F_{zII} = - F\]
\[ \tag{12} M_{bII} = F \cdot (z-a) \]
Grafische Darstellung der Schnittgrößen
Mit den oben berechneten Funktionen ergibt sich folgende Darstellung der Verläufe von Querkraft, Normalkraft und Biegemoment. Die Diagramme sind für den aufwärts gerichteten Teil des Trägers 90° gedreht.
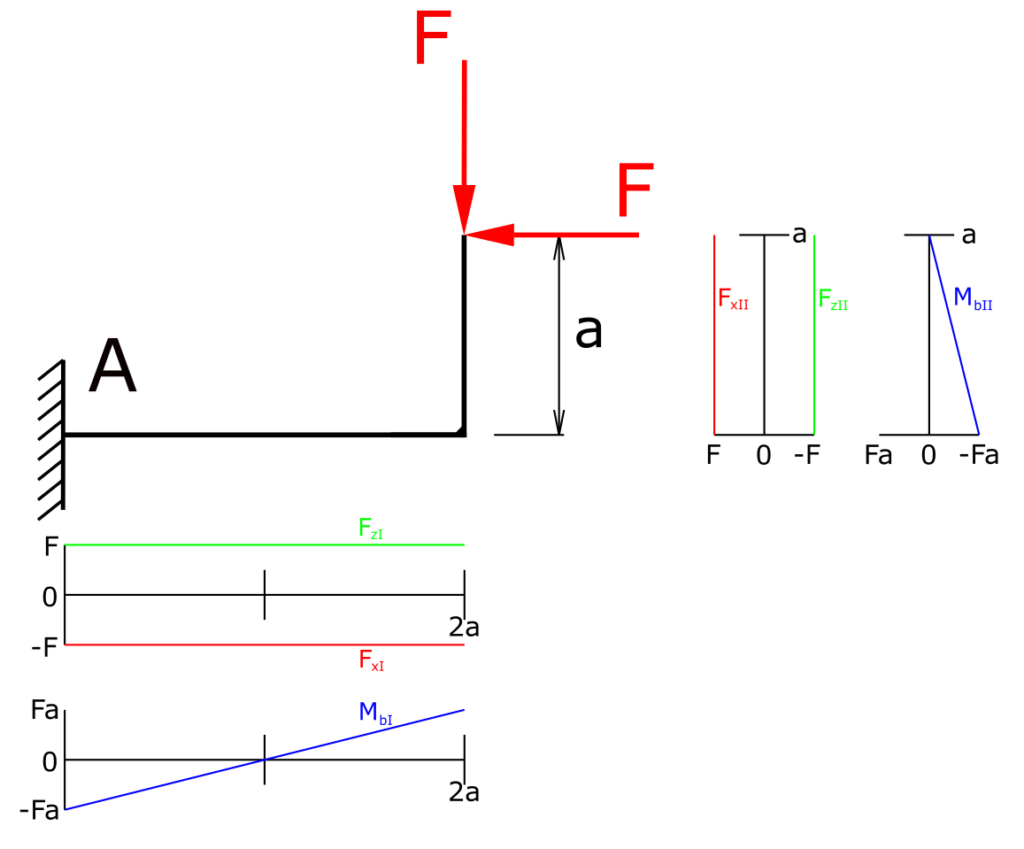
Damit sind alle Schnittgrößen des Trägers ermittelt und visualisiert.
Hier gibt es weitere interessante Aufgaben und Lösungen zum Thema Festigkeitslehre.
Werbung




