Werbung
Diese Übung ist unsere Einstiegsaufgabe in die Festigkeitslehre und beschäftigt sich mit folgenden Fragen:
- Wie berechnet man die Normalkraft in einem Stab?
- Wie stelle ich ein Kräftegleichgewicht mit Schnittgrößen auf?
Aufgabe
Eine Gewichtskraft G2 ist an einem Stab befestigt. Am Verbindungspunkt C wird die Gewichtskraft G1 aufgebracht. Die Stäbe 1 und 2 sind mit Festlagern befestigt. Die Stäbe selbst sind masselos.
Zu berechnen sind die auftretenden Normalkräfte in den Stäben 1 bis 3.
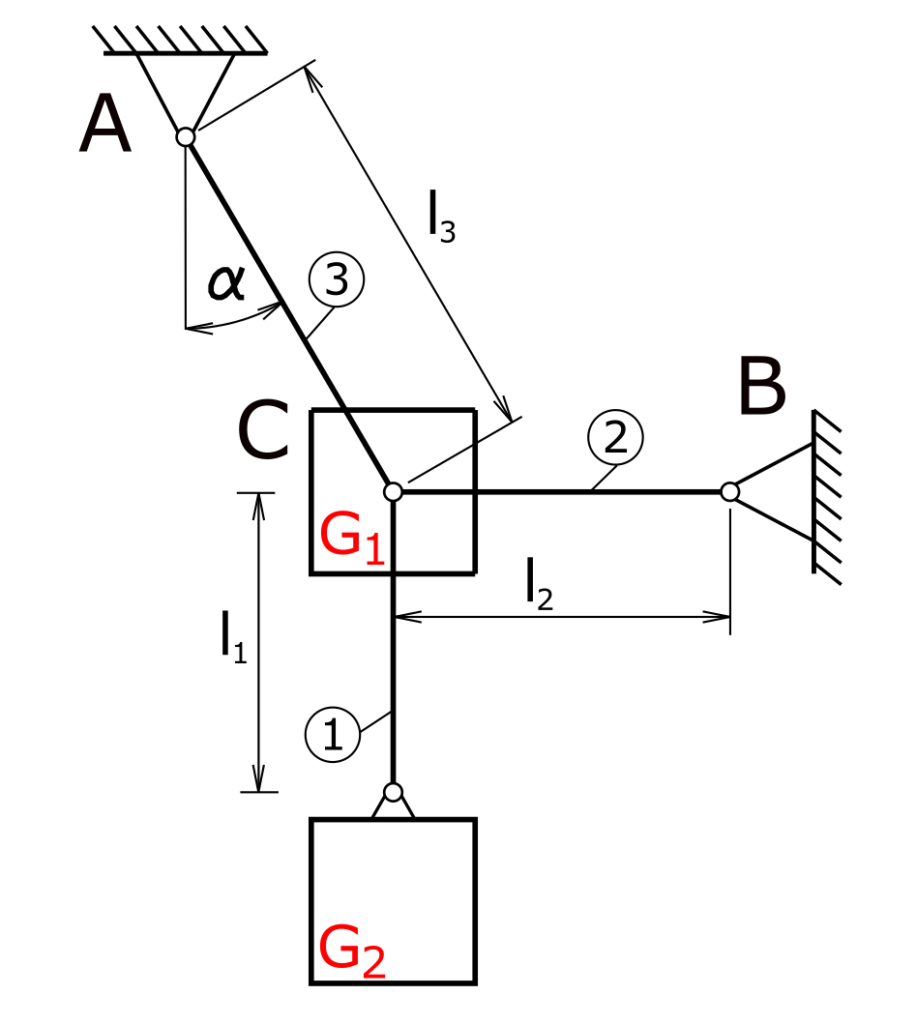
Lösung
Die Normalkräfte werden im Folgenden mit N und dem Index ihrer Stabnummer bezeichnet. Die Normalkraft in Stab 1 lässt sich am einfachsten berechnen.
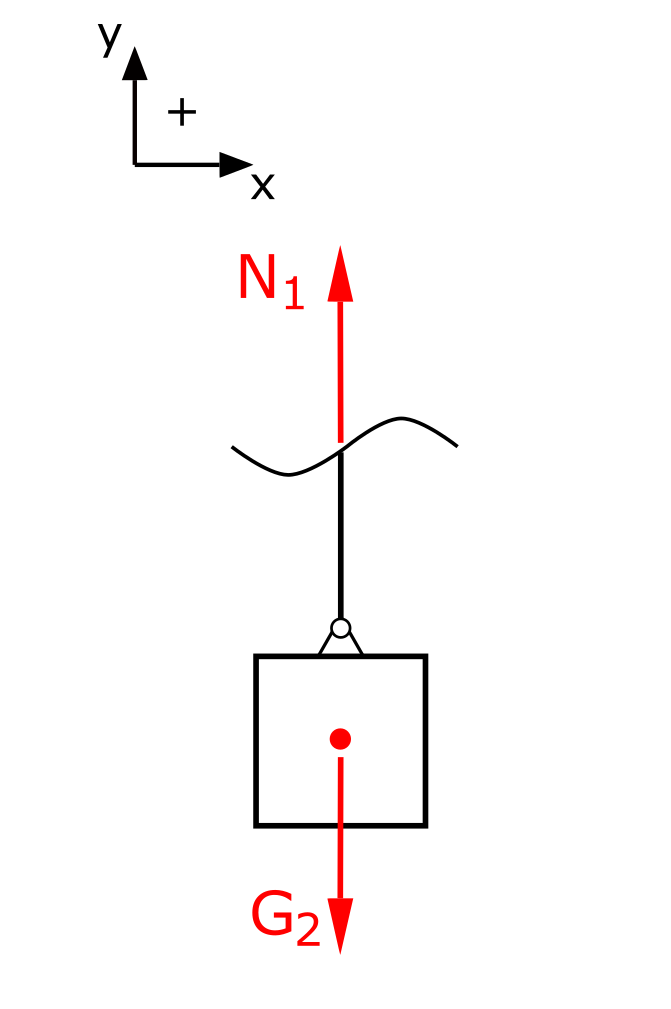
Das Kräftegleichgewicht in y-Richtung liefert
\[ \tag{1} \sum F_y = 0 = N_1 - G_2\]
\[ \tag{2} N_1 = G_2\]
Nun werden, ausgehend von Punkt C, gedanklich die Stäbe durchschnitten und ihre jeweiligen Stabkräfte angetragen. Hier lauert eine kleine Falle in dieser Aufgabe, denn in diesem Freischnitt darf natürlich die Kraft G1 nicht fehlen.
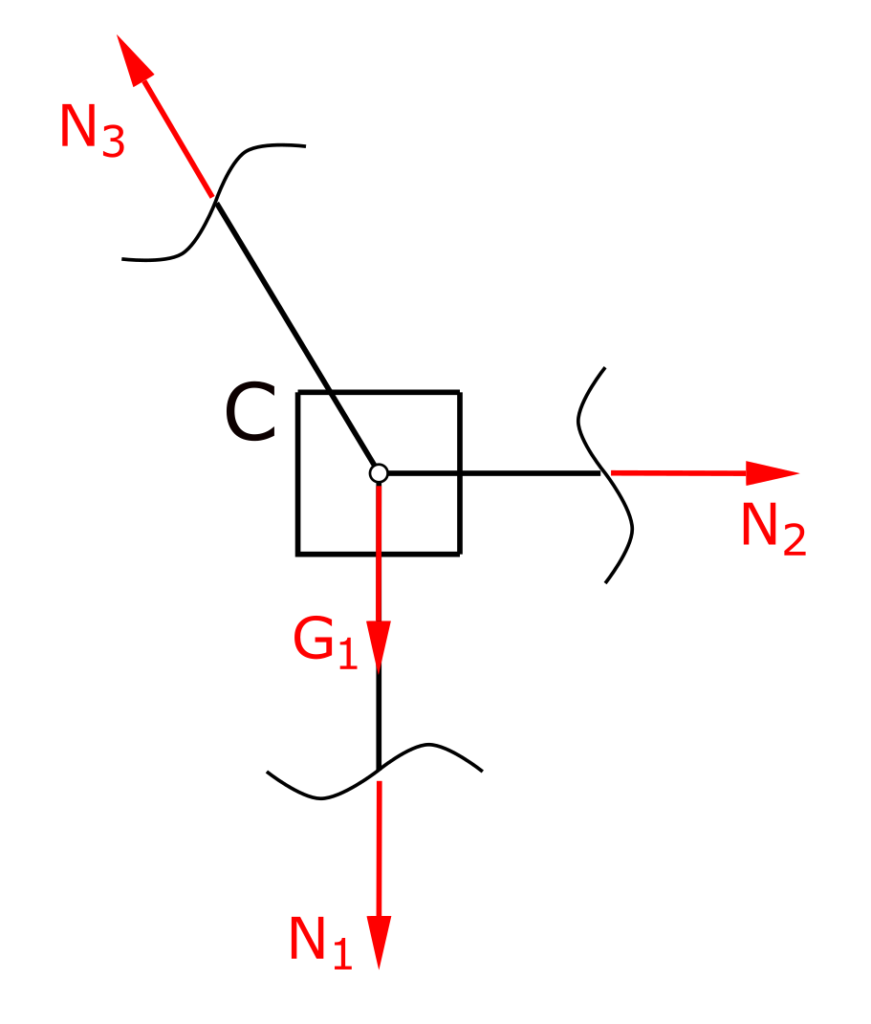
Über die Kräftegleichgewichte in x- und y-Richtung können nun die beiden Normalkräfte in den Stäben 2 und 3 berechnet werden.
\[ \tag{3} \sum F_x = 0 = - N_3 \cdot sin \alpha + N_2\]
\[ \tag{4} \sum F_y = 0 = N_3 \cdot cos \alpha - G_1 - N_1\]
bzw. umgestellt nach N3 und die Normalkraft N1 durch ihren Wert ersetzt:
\[ \tag{5} N_3 = \frac{G_1 + G_2}{cos \alpha} \]
Zum Schluss folgt N2 aus Gleichung 3
\[ \tag{6} N_2 = \frac{G_1 + G_2}{cos \alpha} \cdot sin \alpha\]
oder etwas anders formuliert:
\[ \tag{7} N_2 = (G_1+G_2) \cdot tan \alpha\]
Die in der Aufgabenskizze angegebenen Stablängen waren für die Berechnung der Normalkräfte nicht relevant.
Dies ist die erste Aufgabe aus der Kategorie Technische Mechanik 2. Neben den auf dieser Seite enthaltenen Aufgaben gibt es hier noch eine Sammlung von verschiedenen Aufgaben der Technischen Mechanik 1 bis 3.
Werbung




