Werbung
Diese Übung befasst sich mit den Schnittgrößen bei Streckenlast und behandelt folgende Fragen:
- Wie bestimmt man die Lagerreaktionen eines Trägers mit Streckenlast?
- Wie berechnet man die Schnittgrößen für einen Träger mit Streckenlast?
- Wie berechnet man das maximale Biegemoment eines gleichförmig belasteten Trägers?
Aufgabe
Ein Träger auf zwei Stützen wird durch eine gleichförmige Streckenlast q belastet. Zu ermitteln sind die Lagerreaktionen und die Beanspruchungsgrößen!
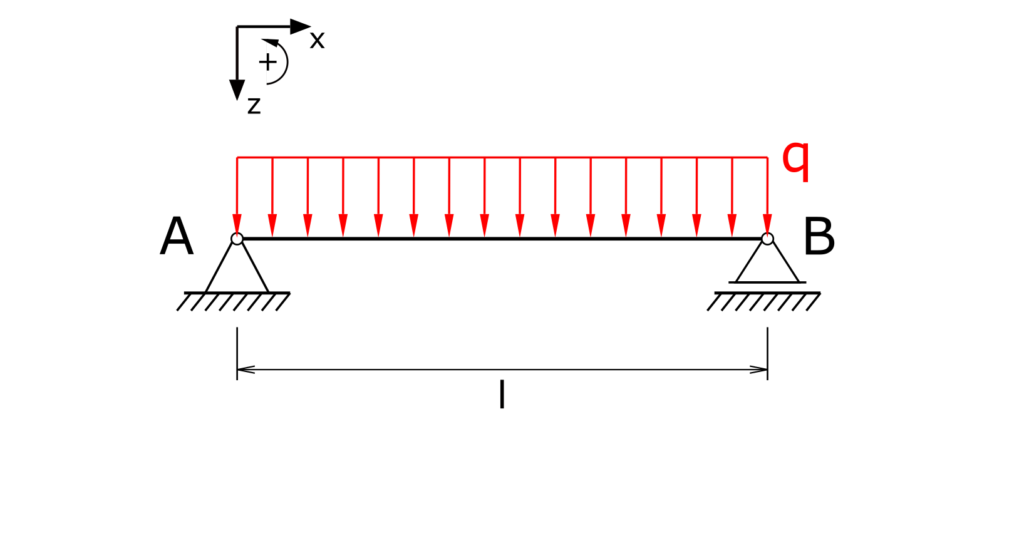
Lösung
Der Träger wird freigeschnitten und die Lagerreaktionen werden angetragen. Auf die Horizontalkomponente des Festlagers wird hier nicht näher eingegangen, da sie offensichtlich Null ist. Die Streckenlast q wird, auch wenn sie hier als konstant gegeben ist, als Funktion aufgefasst. Zu beachten ist die abwärts gerichtete z-Achse!
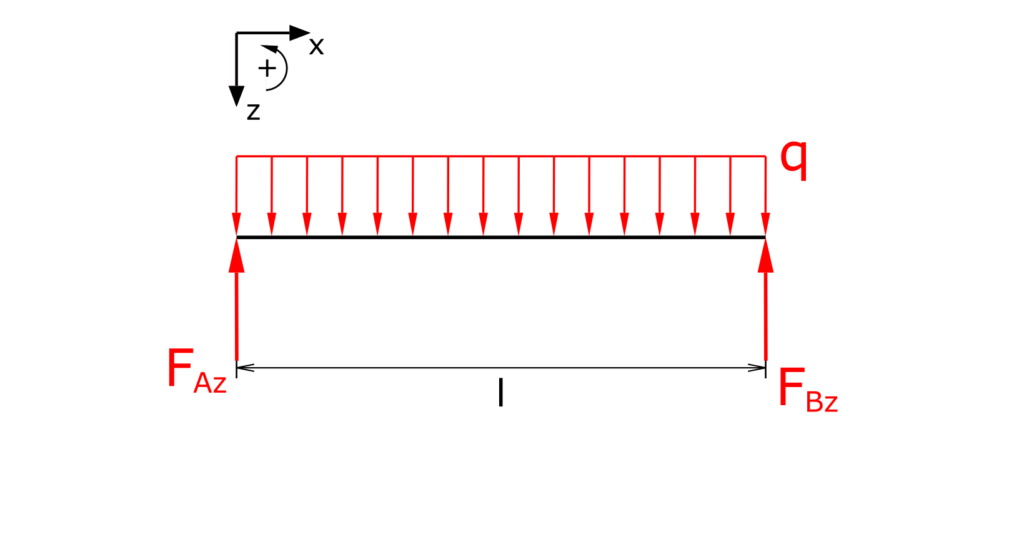
Ermittlung der Lagerreaktionen
Aufstellen der Gleichgewichtsbedingungen für Kräfte in z-Richtung sowie für die Momente:
\[ \tag{1} \sum F_x = 0 \]
\[ \tag{2} \sum F_z = 0 = - F_{Az} + \int_0^l{q(x)dx} - F_{Bz} \]
\[ \tag{3} \sum M(A) = 0 = F_{Bz} \cdot l - \int_0^l{q(x)ldx} \]
Aus Gleichung (3) folgt
\[ \tag{4} F_{Bz} = \frac{q \cdot l}{2} \]
und damit ist
\[ \tag{5} F_{Az} = \frac{q \cdot l}{2} \]
Ermittlung der Schnittgrößen
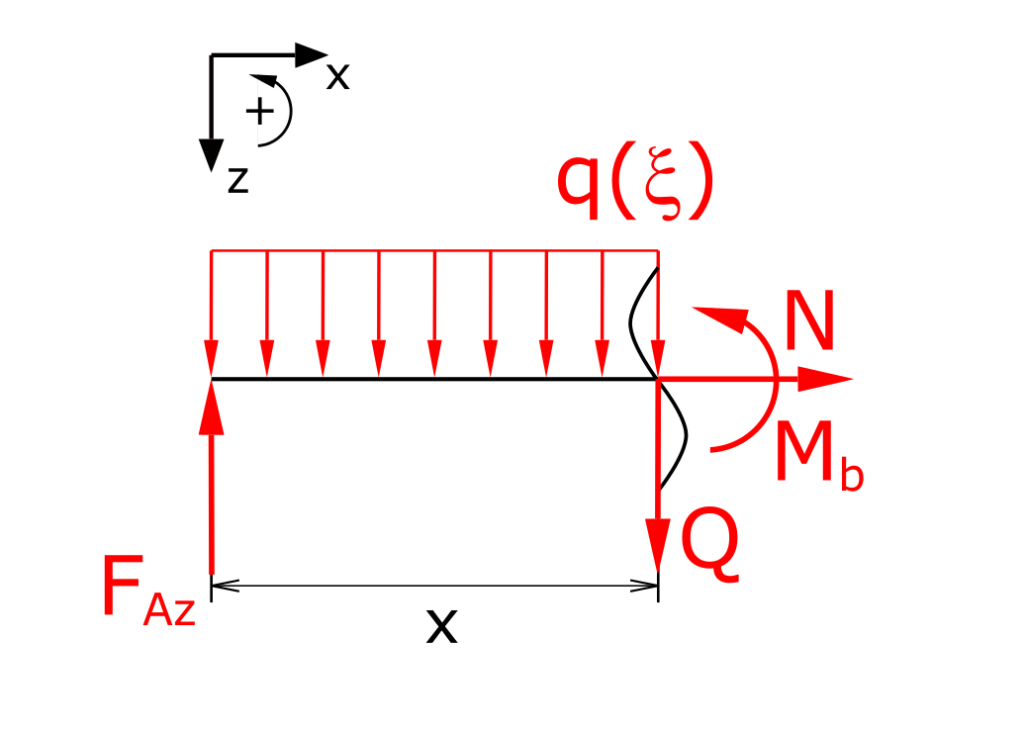
In der o.a. Abbildung sind alle drei Schnittgrößen, also Normalkraft, Querkraft und Biegemoment angegeben. Da die Kräfte in x-Richtung Null sind, ist auch die Normalkraft Null, d.h. sie wird im Folgenden nicht weiter aufgeführt. Die Funktion der Streckenlast erhält die Ersatzkoordinate ξ.
Aufstellen der Gleichgewichtsbedingungen für Kräfte in z-Richtung sowie für die Momente:
\[ \tag{6} \sum F_z = 0 = - F_{Az} + \int_0^x{q(\xi)d\xi} + Q \]
\[ \tag{7} \sum M(x) = 0 = - F_{Az} \cdot x + M_b + \int_0^x{q(\xi)\cdot (x-\xi)d\xi} \]
Die bereits berechnete Lagerreaktion FAz wird in Gleichung (7) eingesetzt.
\[ \tag{8} 0 = - \frac{q \cdot l}{2} \cdot x + M_b + \int_0^x{q(\xi)\cdot (x-\xi)d\xi} \]
Das Biegemoment ergibt sich damit zu
\[ \tag{9} M_b = \frac{q \cdot l}{2} \cdot x - \left[ q \cdot (x\cdot \xi-\frac{\xi^2}{2}) \right]_0^x \]
\[ \tag{10} M_b(x) = \frac{q \cdot x}{2} \cdot (l - x) \]
Damit sind alle erforderlichen Beanspruchungsgrößen ermittelt. Das größte Biegemoment tritt bei diesem Szenario in der Mitte des Trägers auf und beträgt
\[ \tag{11} M_b(x=\frac{l}{2}) = \frac{q \cdot \frac{l}{2}}{2} \cdot (l - \frac{l}{2}) \]
\[ \tag{12} M_b(x=\frac{l}{2}) = \frac{q \cdot l^2}{8} \]
Hier kann man u.a. die Durchbiegung eines Trägers auf zwei Stützen mit gleichförmiger Streckenlast berechnen lassen.
Werbung




