In this exercise we investigate a beam under line load regarding the following questions:
- How to determine the bearing loads of a beam under line load?
- How to determine the internal forces of a beam under line load?
- How to determine the maximum bending moment of an even loaded beam?
Task
A beam on two supports is under load of the even line load q. Determine the bearing reactions and the internal forces!
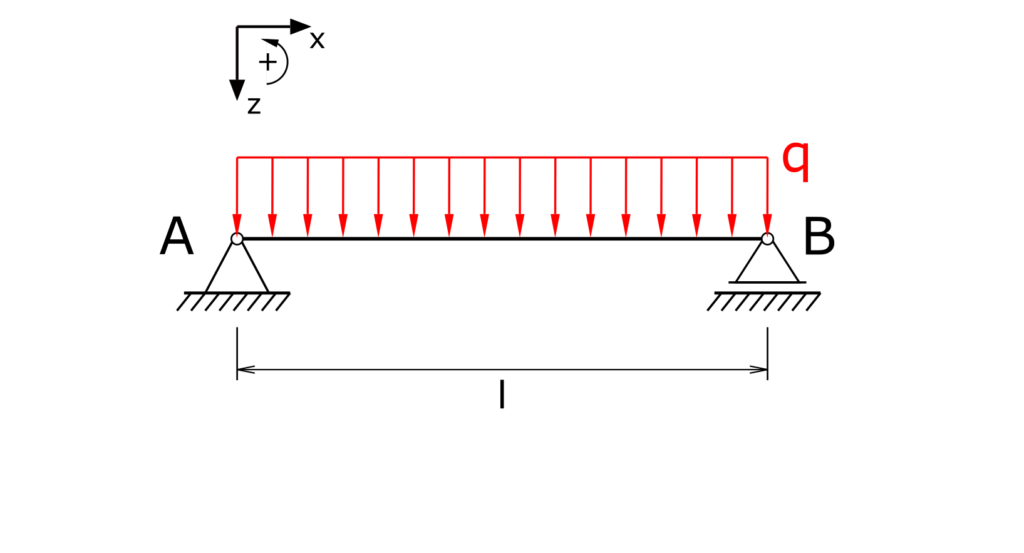
Solution
The beam is cut free and the bearing reactions are drawn. The horizontal component of the fixed bearing is not discussed here, as it is obviously zero. The line load q, even if it is given here as constant, is understood as a function. Note the downward z-axis!
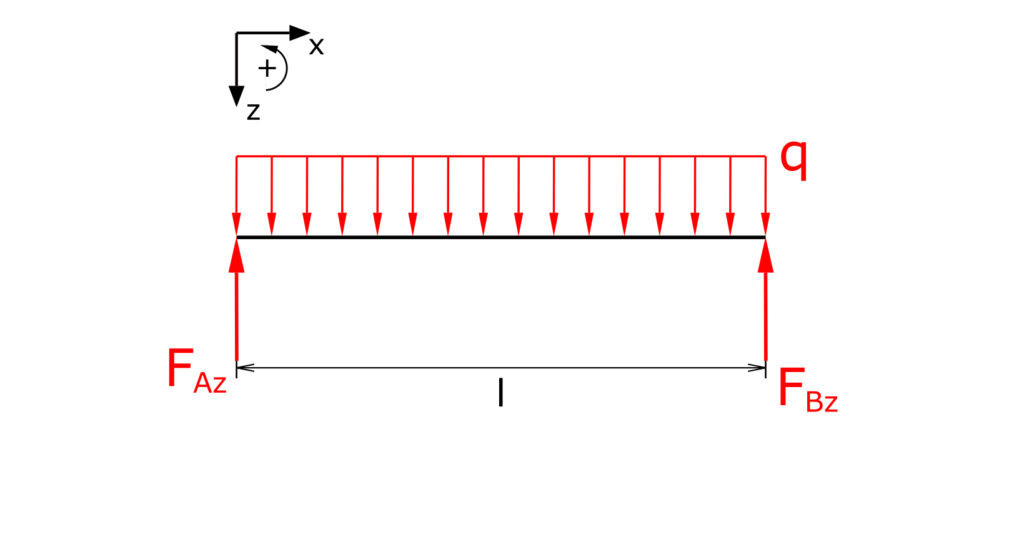
Determination of the bearing reactions
Establishing the equilibrium conditions for forces in the z-direction as well as for the moments:
\[ \tag{1} \sum F_x = 0 \]
\[ \tag{2} \sum F_z = 0 = - F_{Az} + \int_0^l{q(x)dx} - F_{Bz} \]
\[ \tag{3} \sum M(A) = 0 = F_{Bz} \cdot l - \int_0^l{q(x)ldx} \]
From equation (3) follows
\[ \tag{4} F_{Bz} = \frac{q \cdot l}{2} \]
and so it results
\[ \tag{5} F_{Az} = \frac{q \cdot l}{2} \]
Determination of the internal forces
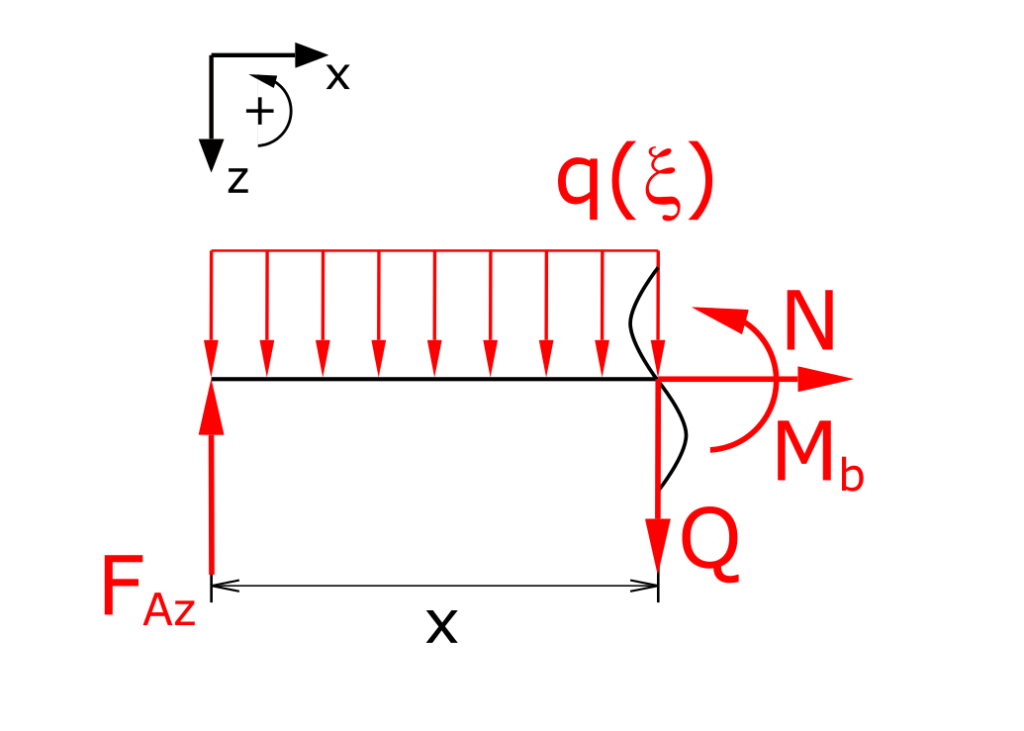
In the above figure, all three internal forces, i.e. normal force, shear force and bending moment, are given. Since the forces in the x-direction are zero, the normal force is also zero, i.e. it is not listed further below. The function of the line load is given the substitute coordinate ξ.
Establishing the equilibrium conditions for forces in the z-direction as well as for the moments:
\[ \tag{6} \sum F_z = 0 = - F_{Az} + \int_0^x{q(\xi)d\xi} + Q \]
\[ \tag{7} \sum M(x) = 0 = - F_{Az} \cdot x + M_b + \int_0^x{q(\xi)\cdot (x-\xi)d\xi} \]
The already known bearing load FAz is used now in equation (7).
\[ \tag{8} 0 = - \frac{q \cdot l}{2} \cdot x + M_b + \int_0^x{q(\xi)\cdot (x-\xi)d\xi} \]
The bending moment results to
\[ \tag{9} M_b = \frac{q \cdot l}{2} \cdot x - \left[ q \cdot (x\cdot \xi-\frac{\xi^2}{2}) \right]_0^x \]
\[ \tag{10} M_b(x) = \frac{q \cdot x}{2} \cdot (l - x) \]
In this way, all the required stress parameters are determined. In this scenario, the highest bending moment occurs in the center of the beam and is
\[ \tag{11} M_b(x=\frac{l}{2}) = \frac{q \cdot \frac{l}{2}}{2} \cdot (l - \frac{l}{2}) \]
\[ \tag{12} M_b(x=\frac{l}{2}) = \frac{q \cdot l^2}{8} \]
Here you can calculate the deflection of a beam on two supports with an even line load.

