Werbung
Die nachfolgende Aufgabe beschäftigt sich mit folgenden Fragen:
- Wie berücksichtigt man Ausschnitte in Querschnitten bei der Schwerpunktberechnung?
- Wie berechnet man den Flächenschwerpunkt mit Bohrung?
Aufgabe
Für den dargestellten Kreisquerschnitt mit Bohrung soll der gemeinsame Flächenschwerpunkt berechnet werden.
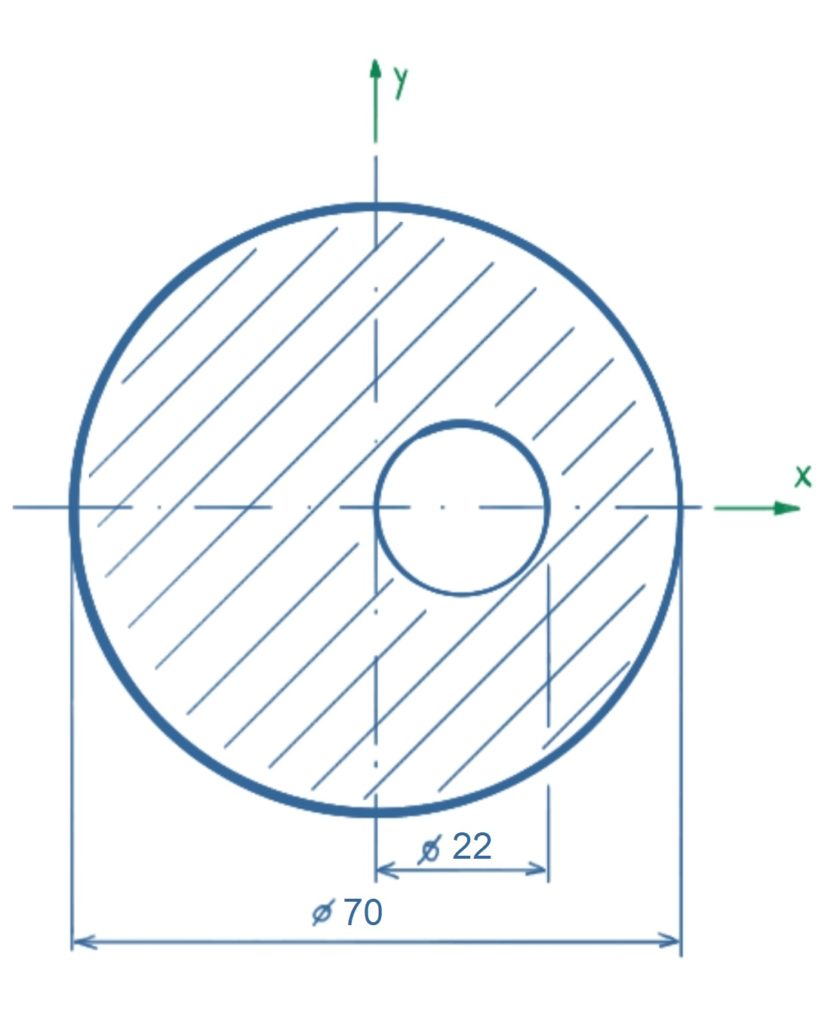
Lösung
Die einzelnen Flächen werden im ersten Schritt nummeriert.
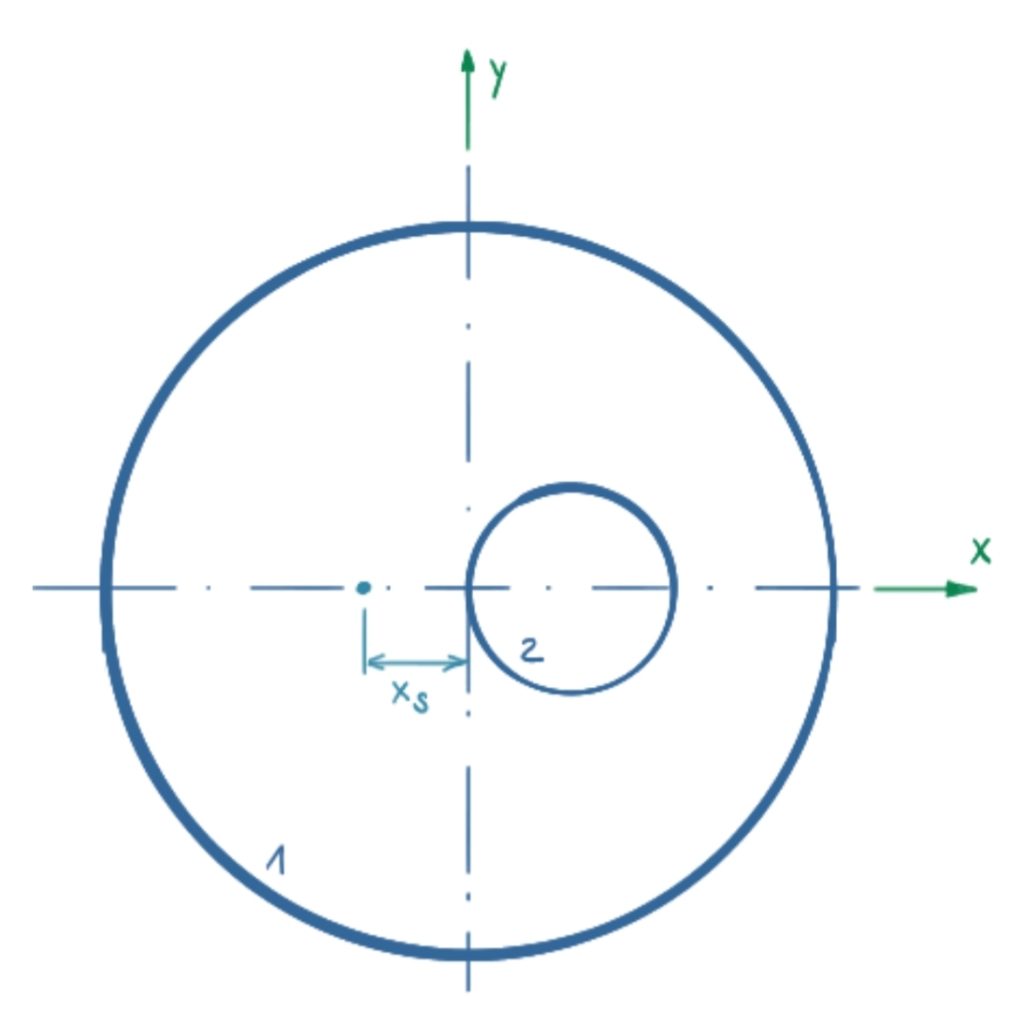
Da das Bauteil spiegelsymmetrisch um die x-Achse ist, genügt eine Betrachtung der x-Koordinate. Die allgemeine Gleichung für die x-Koordinate des Schwerpunkts lautet:
\[ \tag{1} x_S = \frac{\sum A_i \cdot x_i}{\sum A_i} \]
Und für die Fläche des Kreises
\[ \tag{2} A = \frac{\pi}{4} \cdot d^2 \]
Die einzelnen Flächeninhalte und Einzelschwerpunkte werden in einer Tabelle aufgeführt. Dabei gehen leere Flächen, also wie z.B. die Bohrung mit dem Durchmesser 22mm, negativ ein.
| \[ i \] | \[ A_i \] | \[ x_i \, in \, mm \] | \[ A_i \cdot x_i\, in \,mm^3 \] |
|---|---|---|---|
| 1 | 3.848 | 0 | 0 |
| 2 | -380 | 11 | -4.180 |
| \[ \sum \] | 3.468 | -4.180 |
\[ \tag{3} x_S = \frac{-4180mm^3}{3468mm^2} \]
\[ \tag{4} x_S = -1,21 mm \]
Und der Vollständigkeit halber:
\[ \tag{5} y_S = 0 mm \]
Weitere Aufgaben zum Thema Schwerpunkt gibt es unter dem Schlagwort Schwerpunkt.
Werbung




