Werbung
In dieser Übung wird die Kinematik des Kurbeltriebs betrachtet und die Funktionen zur Berechnung der Kolbengeschwindigkeit und der Kolbenbeschleunigung aufgestellt. Hier gibt es ein Excel-Berechnungsblatt zur Berechnung der kinematischen Parameter eines Kurbeltriebs auf Basis der hier gezeigten Berechnungsgleichungen.
Aufgabe
Für einen Kurbeltrieb einer Kolbenmaschine sind Geschwindigkeit und Beschleunigung des Kolbens zu berechnen. Die Kurbel dreht sich mit einer konstanten Winkelgeschwindigkeit ω.
Für das Verhältnis von Pleuellänge r und Länge der Schubkurbel l soll gelten
\[ l \gg r \]
Lösung
Die Winkelgeschwindigkeit ist
\[ \tag{1} \omega = \frac{\varphi}{t} \]
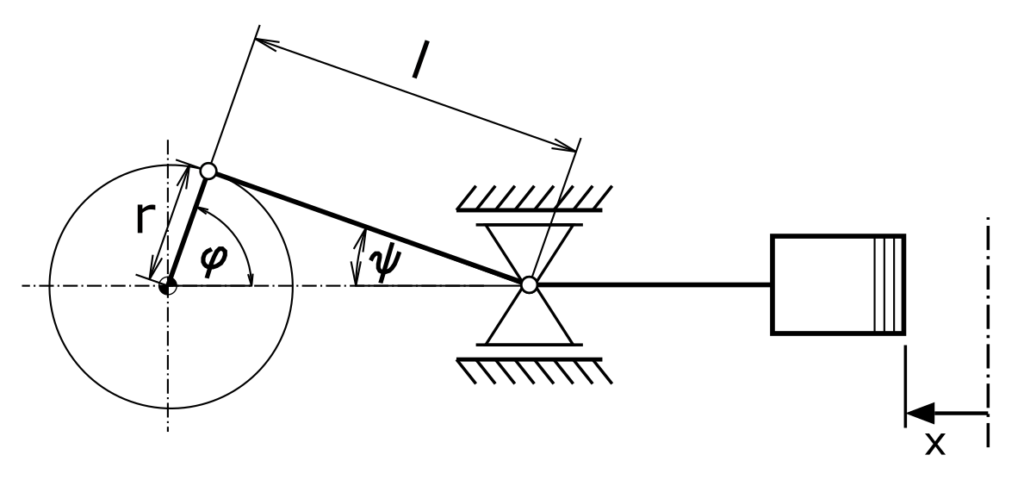
Der geometrische Zusammenhang zwischen Drehwinkel φ und Kolbenposition x lautet:
\[ \tag{2} r + l = r \cdot cos \varphi + l \cdot cos \psi + x \]
Dabei ist
\[ \tag{3} r \cdot sin \varphi = l \cdot sin \psi \]
Zur Vereinfachung der Rechnung wird das Verhältnis der Längen wie folgt ausgedrückt:
\[ \tag{4} \frac{r}{l} = \lambda \]
Damit ergibt sich
\[ \tag{5} \frac{x}{r} = \left( 1 - cos \varphi \right) + \frac{1}{\lambda} \left( 1-\sqrt{1-\lambda^2 sin^2 \varphi} \right) \]
Die Geschwindigkeit ist
\[ \tag{6} \dot{x} = \frac{dx}{d\varphi} \frac{d\varphi}{dt} = \frac{dx}{d\varphi} \omega \]
\[ \tag{7} \frac{\dot{x}}{r \omega} = sin \varphi + \lambda \frac{sin \varphi \cdot cos \varphi}{\sqrt{1-\lambda^2 sin^2 \varphi}} \]
Es gilt
\[ \tag{8} \lambda \ll 1 \]
und der Ausdruck
\[ \tag{9} \frac{1}{\sqrt{1-\lambda^2 sin^2 \varphi}} \]
kann in eine Potenzreihe entwickelt werden.
\[ \tag{10} \frac{1}{\sqrt{1-\lambda^2 sin^2 \varphi}} = 1 + \frac{1}{2} \lambda^2 sin^2 \varphi + \frac{3}{8} \lambda^4 sin^4 \varphi \, + ... \]
Berücksichtigt man nur die Glieder bis zur 1. Potenz von λ, so ergibt sich aus Gleichung (7)
\[ \tag{11} \frac{\dot{x}}{r \omega} = sin \varphi + \lambda \cdot sin \varphi \cdot cos \varphi = sin \varphi + \frac{\lambda}{2}sin 2 \varphi \]
Die Kolbengeschwindigkeit beträgt also
\[ \tag{12} \dot{x} = r \omega \left( sin \varphi + \frac{\lambda}{2}sin 2 \varphi \right) \]
Die Beschleunigung ist
\[ \tag{13} \ddot{x} = \frac{d^2x}{d \varphi^2}\omega^2 \]
\[ \tag{14} \frac{\ddot{x}}{r \omega^2} = cos \varphi + \lambda \frac{cos^2 \varphi -sin^2\varphi \left( 1-\lambda^2 sin^2\varphi \right)}{\left( 1 - \lambda^2 sin^2 \varphi \right)^{\frac{3}{2}}} \]
Für λ viel kleiner als 1 ergibt sich
\[ \tag{15} \frac{\ddot{x}}{r \omega^2} = cos \varphi + \lambda \cos 2 \varphi \]
bzw.
\[ \tag{16} \ddot{x} = r \omega^2 \left( cos \varphi + \lambda \cos 2 \varphi \right) \]
Damit sind Geschwindigkeit und Beschleunigung des Kolbens beim Kurbeltrieb bestimmt.
Werbung




