In this exercise, the kinematics of a crank drive are considered and the functions for the piston speed and piston acceleration are set up.
Task
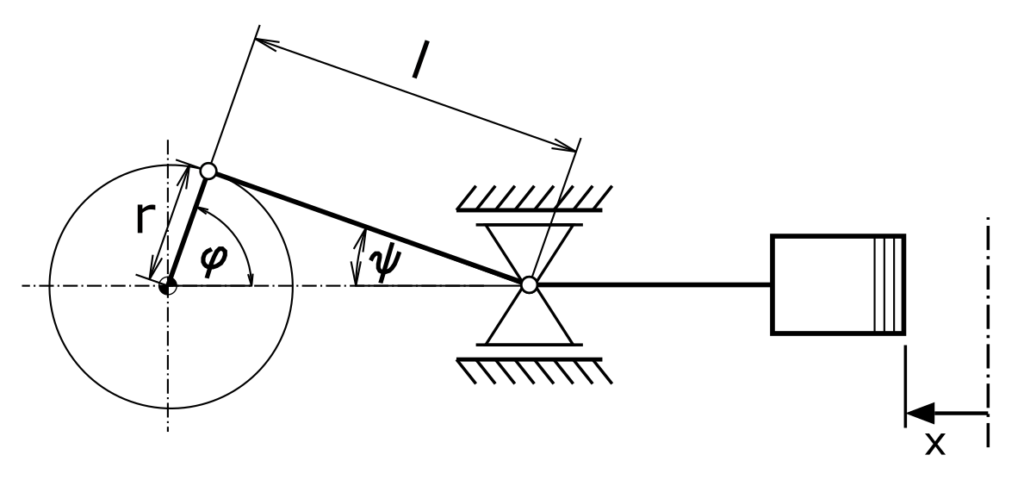
For a crank drive of a piston machine, the speed and acceleration of the piston have to be calculated. The crank rotates at a constant angular velocity ω. For the ratio of the connecting rod length r and the length of the slider crank l should apply
\[ l \gg r \]
Solution
The angular velocity is
\[ \tag{1} \omega = \frac{\varphi}{t} \]
The geometric relationship between the angle of rotation φ and the piston position x is:
\[ \tag{2} r + l = r \cdot cos \varphi + l \cdot cos \psi + x \]
It is
\[ \tag{3} r \cdot sin \varphi = l \cdot sin \psi \]
To simplify the calculation, the ratio of the lengths is expressed as follows:
\[ \tag{4} \frac{r}{l} = \lambda \]
This results in
\[ \tag{5} \frac{x}{r} = \left( 1 - cos \varphi \right) + \frac{1}{\lambda} \left( 1-\sqrt{1-\lambda^2 sin^2 \varphi} \right) \]
The velocity is
\[ \tag{6} \dot{x} = \frac{dx}{d\varphi} \frac{d\varphi}{dt} = \frac{dx}{d\varphi} \omega \]
\[ \tag{7} \frac{\dot{x}}{r \omega} = sin \varphi + \lambda \frac{sin \varphi \cdot cos \varphi}{\sqrt{1-\lambda^2 sin^2 \varphi}} \]
It applies
\[ \tag{8} \lambda \ll 1 \]
and the term
\[ \tag{9} \frac{1}{\sqrt{1-\lambda^2 sin^2 \varphi}} \]
can be expanded into a power series.
\[ \tag{10} \frac{1}{\sqrt{1-\lambda^2 sin^2 \varphi}} = 1 + \frac{1}{2} \lambda^2 sin^2 \varphi + \frac{3}{8} \lambda^4 sin^4 \varphi \, + ... \]
If one only takes into account the terms up to the 1st power of λ, then from equation (7)
\[ \tag{11} \frac{\dot{x}}{r \omega} = sin \varphi + \lambda \cdot sin \varphi \cdot cos \varphi = sin \varphi + \frac{\lambda}{2}sin 2 \varphi \]
The piston velocity thus is
\[ \tag{12} \dot{x} = r \omega \left( sin \varphi + \frac{\lambda}{2}sin 2 \varphi \right) \]
The acceleration is
\[ \tag{13} \ddot{x} = \frac{d^2x}{d \varphi^2}\omega^2 \]
\[ \tag{14} \frac{\ddot{x}}{r \omega^2} = cos \varphi + \lambda \frac{cos^2 \varphi -sin^2\varphi \left( 1-\lambda^2 sin^2\varphi \right)}{\left( 1 - \lambda^2 sin^2 \varphi \right)^{\frac{3}{2}}} \]
For λ much smaller than 1 we get
\[ \tag{15} \frac{\ddot{x}}{r \omega^2} = cos \varphi + \lambda \cos 2 \varphi \]
respectively
\[ \tag{16} \ddot{x} = r \omega^2 \left( cos \varphi + \lambda \cos 2 \varphi \right) \]
So the determination of the speed and the acceleration of the piston in the crank drive is complete.

