Werbung
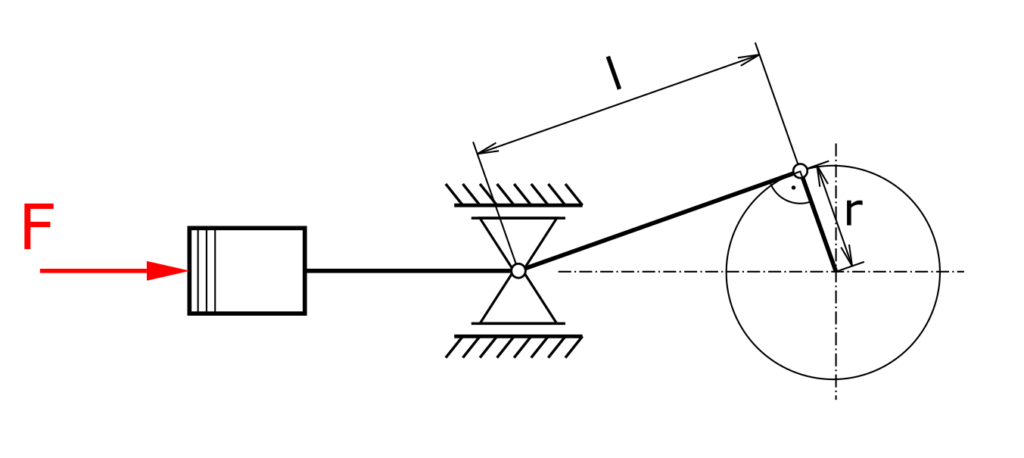
Diese Übung befasst sich mit einer statischen Betrachtung der Kräfte am Kurbeltrieb mit Kreuzkopflagerung für einen bestimmten Drehwinkel. Hier gibt es eine Aufgabe zur Kinematik des Kurbeltriebs.
Aufgabe
Auf den Kolben einer Dampfmaschine wirkt die Kraft F. Zu berechnen sind
a) die Kraft in der Schubstange,
b) die Querkraft in der Kreuzkopflagerung und
c) das Drehmoment in der Kurbelwelle.
Lösung
Lösungsskizze
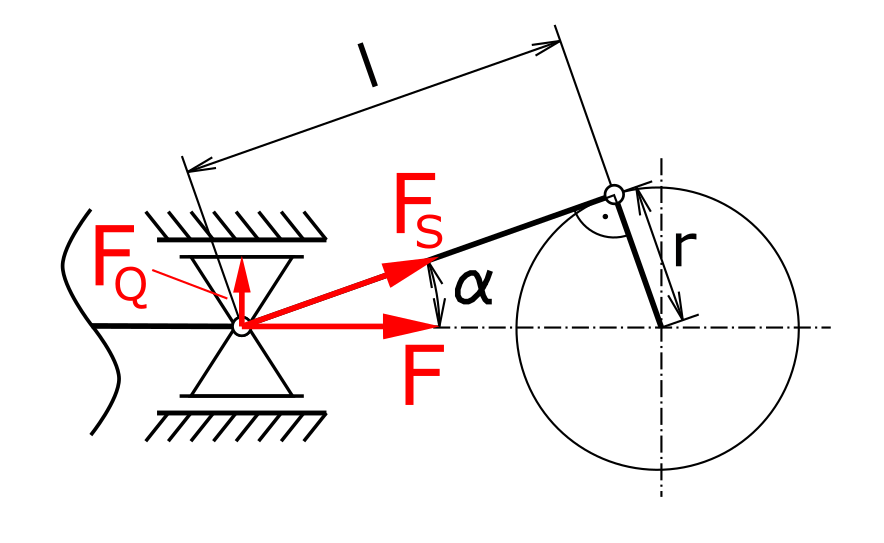
Der Winkel α zwischen der Kraft F und der Schubstange ergibt sich aus
\[\tag{1} \alpha = arctan \left( \frac{r}{l} \right) \]
Zwischen Schubstangenkraft und Kolbenkraft besteht die Beziehung
\[\tag{2} F = F_S \cdot \cos \alpha \]
\[\tag{3} F_S = \frac{F}{\cos \alpha} \]
Der Kosinus vom Arkustangens α führt zu
\[\tag{4} \cos \left( arctan \left( \frac{r}{l} \right) \right) = \frac{1}{\sqrt{\left( \frac{r}{l}\right)^2 + 1}} \]
Damit beträgt die Kraft in der Schubstange
\[\tag{5} F_S = F \cdot \sqrt{\left( \frac{r}{l}\right)^2 + 1} \]
Die Querkraft in der Kreuzkopflagerung ergibt sich aus
\[\tag{6} F_Q = F_S \cdot \sin \alpha \]
Der Sinus vom Arkustangens α führt zu
\[\tag{7} \sin \left( arctan \left( \frac{r}{l} \right) \right) = \frac{\frac{r}{l}}{\sqrt{\left( \frac{r}{l}\right)^2 + 1}} \]
Damit beträgt die Querkraft
\[\tag{8} F_Q = F \cdot \bcancel{\sqrt{\left( \frac{r}{l}\right)^2 + 1}} \cdot \frac{\frac{r}{l}}{\bcancel{\sqrt{\left( \frac{r}{l}\right)^2 + 1}}} \]
\[\tag{9} F_Q = F \cdot \frac{r}{l} \]
Das Moment an der Kurbelwelle beträgt
\[\tag{10} M_K = F_S \cdot r \]
\[\tag{11} M_K = F \cdot r \cdot \sqrt{\left( \frac{r}{l}\right)^2 + 1} \]
Hier gibt es eine Übersicht über Reaktionskräfte von Auflagern, Gelenken und Führungen.
Werbung




