This exercise is about a statics investigation of the forces on a crank drive with a crosshead guidance for a specified rotation angle. The kinematics of a crank drive is considered here.
Task
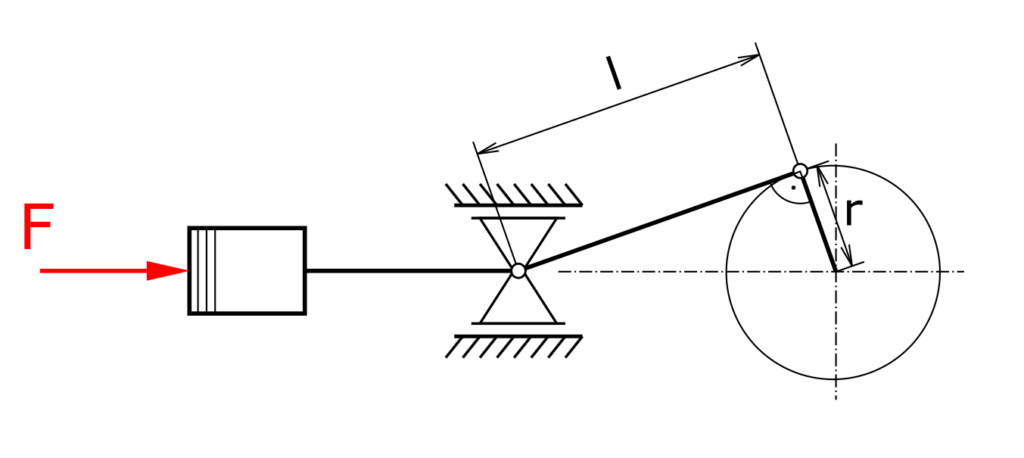
The force F acts on the piston of a steam engine. The following parameters have to be calculated:
a) the force in the driving rod,
b) the transverse force in the crosshead guidance (crosshead bearing) and
c) the torque in the crankshaft.
Solution
The following video is in german language.
Sketch for the solution
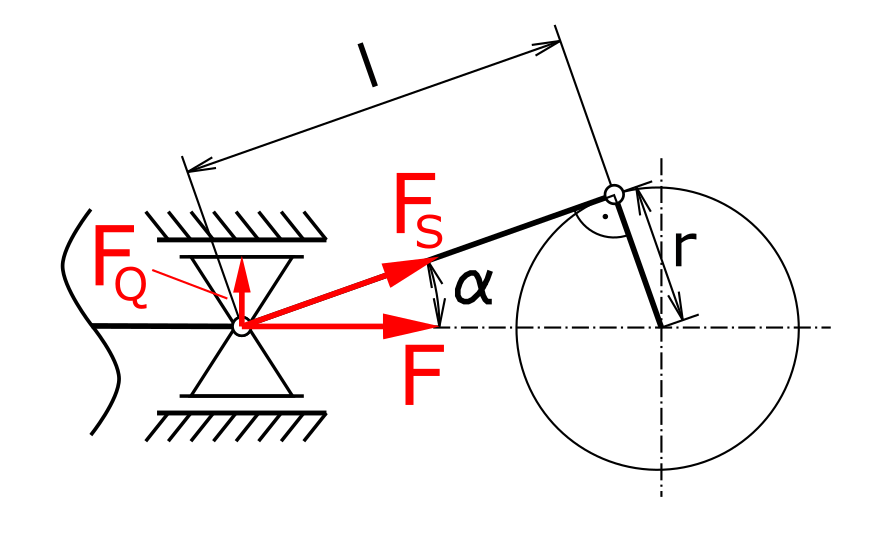
The angle α between the force F and the driving rod results from
\[\tag{1} \alpha = arctan \left( \frac{r}{l} \right) \]
Between the force F and the force FS in the driving rod exists the following relationship
\[\tag{2} F = F_S \cdot \cos \alpha \]
\[\tag{3} F_S = \frac{F}{\cos \alpha} \]
The cosine of the arctangent α leads to
\[\tag{4} \cos \left( arctan \left( \frac{r}{l} \right) \right) = \frac{1}{\sqrt{\left( \frac{r}{l}\right)^2 + 1}} \]
So this is the force in the driving rod:
\[\tag{5} F_S = F \cdot \sqrt{\left( \frac{r}{l}\right)^2 + 1} \]
The transversal force in the crosshead guiding results from
\[\tag{6} F_Q = F_S \cdot \sin \alpha \]
The sine of the arctangent α leads to
\[\tag{7} \sin \left( arctan \left( \frac{r}{l} \right) \right) = \frac{\frac{r}{l}}{\sqrt{\left( \frac{r}{l}\right)^2 + 1}} \]
So the transversal force is
\[\tag{8} F_Q = F \cdot \bcancel{\sqrt{\left( \frac{r}{l}\right)^2 + 1}} \cdot \frac{\frac{r}{l}}{\bcancel{\sqrt{\left( \frac{r}{l}\right)^2 + 1}}} \]
\[\tag{9} F_Q = F \cdot \frac{r}{l} \]
The torque at the crankshaft is
\[\tag{10} M_K = F_S \cdot r \]
\[\tag{11} M_K = F \cdot r \cdot \sqrt{\left( \frac{r}{l}\right)^2 + 1} \]
This exercise is part of the collection Engineering Mechanics 1 - Statics.

