Werbung
Diese Übung zeigt, wie man die Lagerreaktionen der festen Einspannung berechnet, am Beispiel eines Kragträgers.
Aufgabe
Ein im Punkt A einseitig eingespannter Träger wird mit den Kräften F1 und F2 belastet. Welche Lagerreaktionen treten in A auf?
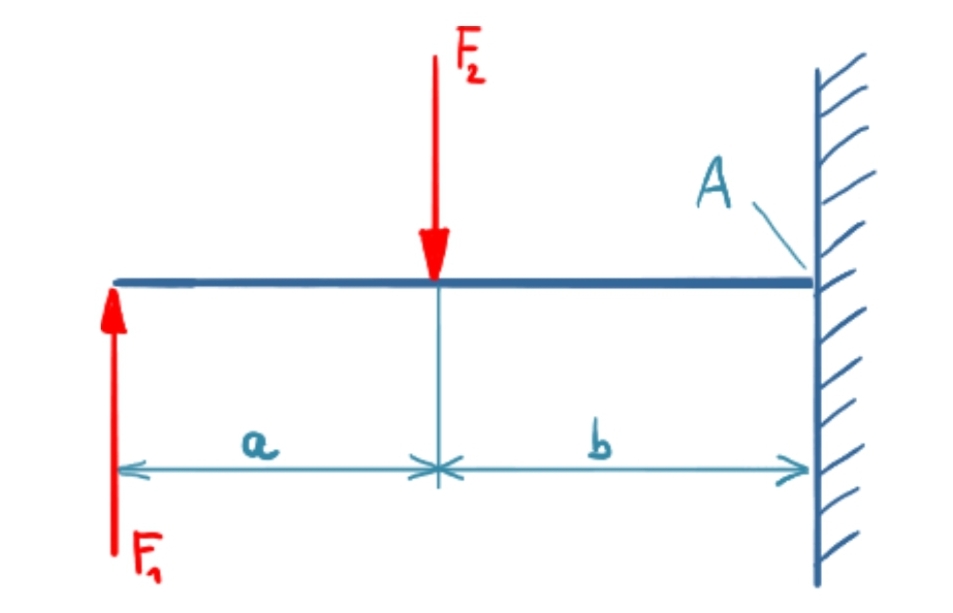
Lösung
Freigeschnittener Träger
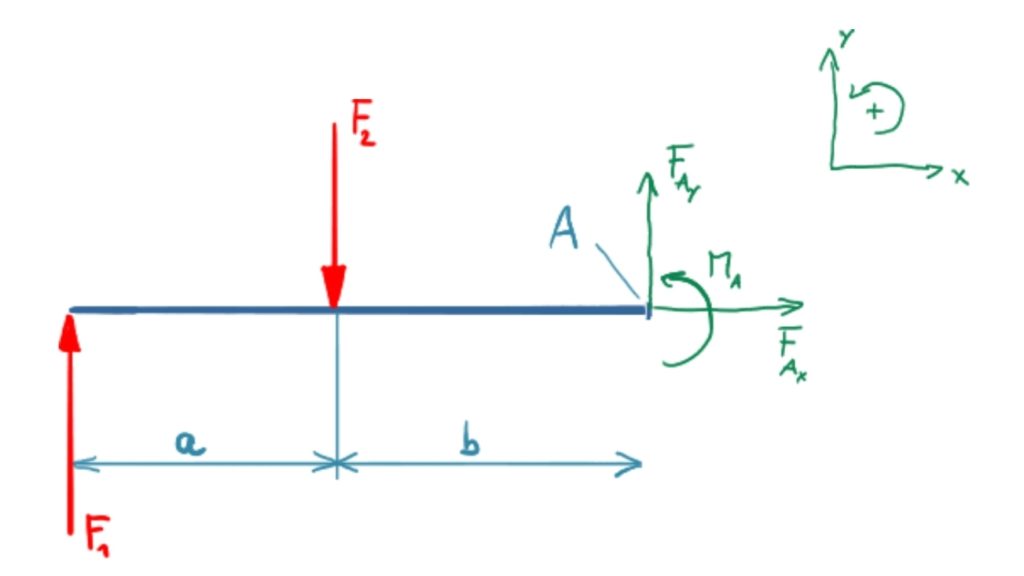
In dieser Aufgabe ist das einzige Lager eine feste Einspannung. Diese Form von Trägern nennt man Kragträger. In der Praxis kommen sie bspw. vor, wenn in einem Getriebe ein Zahnrad auf einer einseitig gelagerten Achse läuft. Die Lagerreaktionen lassen sich wie folgt bestimmen (linksdrehende Momente sind positiv):
\[ \require{cancel} \] \[ \newcommand{\myvec}[1]{{\begin{pmatrix}#1\end{pmatrix}}} \]Das Kräftegleichgewicht in x-Richtung ist
\[\tag{1} \sum F_x = 0 = F_{Ax} \]
Das Kräftegleichgewicht in y-Richtung ist
\[\tag{2} \sum F_y = 0 = F_1 - F_2 + F_{Ay} \]
\[\tag{3} F_{Ay} = F_2 - F_1 \]
Das Momentengleichgewicht um Punkt A ist
\[\tag{4} \sum M(A) = 0 = -F_1 \cdot (a+b) + F_2 \cdot b + M_A \]
\[\tag{5} M_A = F_1 \cdot (a+b) - F_2 \cdot b \]
Damit sind die Lagerreaktionen der festen Einspannung bestimmt.
Hier gibt es eine weitere Übungsaufgabe, in der gezeigt wird, wie man die Biegelinie für den oben dargestellten Kragträger mit zwei entgegengesetzt wirkenden Kräften ermittelt. Dort wird allerdings angenommen, dass die beiden Kräfte gleich groß sind und dass der Abstand zwischen den beiden Kräften genau so groß ist, wie der Abstand von der ersten Kraft bis zur festen Einspannung.
Werbung




