Werbung
In dieser Übung wird die Biegelinie für einen einseitig eingespannten Träger mit zwei entgegengesetzten Lasten entsprechend der Bernoulli-Balkenbiegung berechnet.
Aufgabe
Ein einseitig fest eingespannter Träger wird durch die entgegengesetzten Kräfte F belastet. Es ist die Biegelinie für den Träger zu bestimmen!
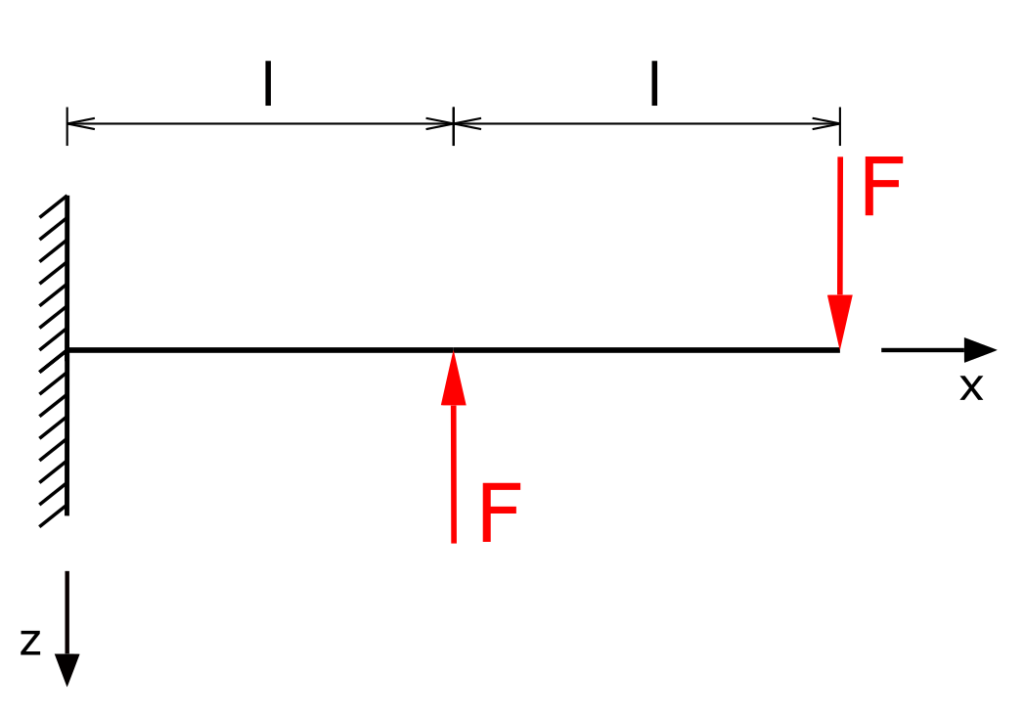
Lösung
Zur Bestimmung der Biegelinie müssen die Schnittgrößen des Trägers ermittelt werden. Dabei ist für die Biegung nur das Biegemoment relevant, d.h. in den folgenden Gleichungen werden auch nur die Momentengleichgewichte aufgestellt. Der Träger wird in zwei Bereiche eingeteilt.
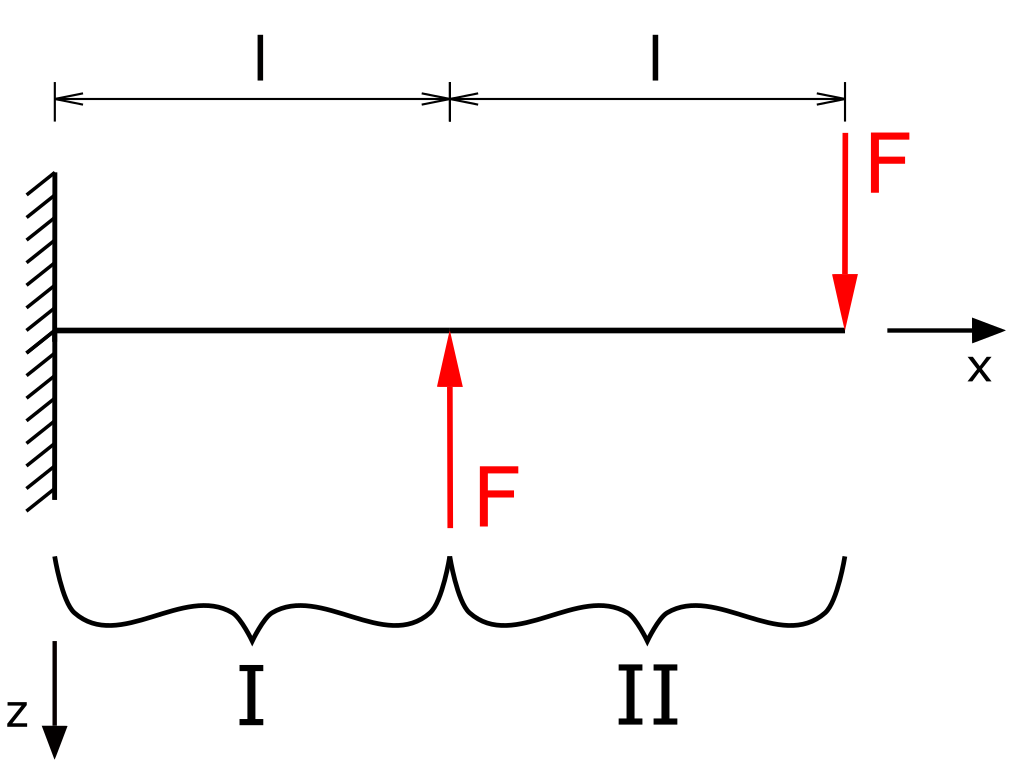
Es ist in diesem Fall nicht erforderlich, die Lagerreaktionen der festen Einspannung zu ermitteln, so dass unmittelbar mit den Schnittgrößen für Bereich I begonnen werden kann.
Bestimmung der Biegemomente
Linksdrehende Momente sind im Folgenden positiv. Die Schnittgrößen werden an einem negativen Schnittufer negativ angetragen.
Bereich I
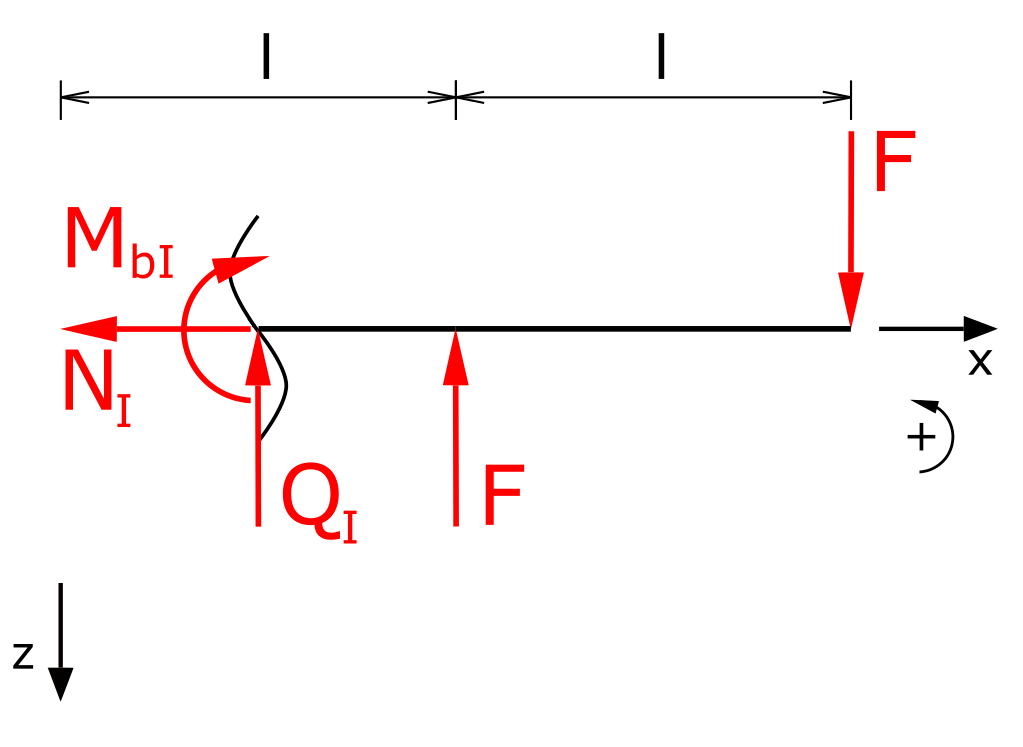
Die Momentenbilanz in Bereich I lautet
\[ \tag{1} \sum M(x) = 0 = -M_{bI} + F \cdot (l-x) - F \cdot (2 \cdot l -x) \]
\[ \tag{2} M_{bI} = - F \cdot l \]
Bereich II
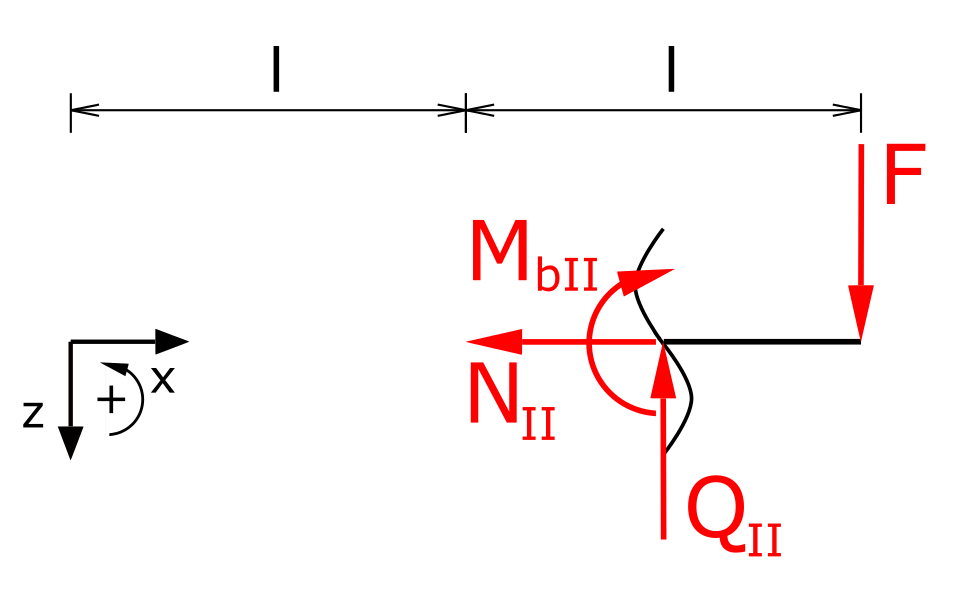
Die Momentenbilanz in Bereich II lautet
\[ \tag{3} \sum M(x) = 0 = -M_{bII} - F \cdot (2 \cdot l -x) \]
\[ \tag{4} M_{bI} = F \cdot x - 2 \cdot F \cdot l \]
Biegelinien
Die Biegelinien werden auf Basis der Bernoulli-Balkenbiegung bestimmt. Der grundsätzliche Zusammenhang lautet
\[ w'' = \frac{-M_b}{E \cdot I} \]
Dabei ist w'' die zweite Ableitung der Biegelinie, E der Elastizitätsmodul und I das Flächenträgheitsmoment. Die Biegelinie w erhält man durch zweifache Integration. Daraus folgt für den vorliegenden Fall
Bereich I
\[ \tag{5} E \cdot I \cdot w''_I = F \cdot l \]
\[ \tag{6} E \cdot I \cdot w'_I = F \cdot l \cdot x + c_1\]
\[ \tag{7} E \cdot I \cdot w_I = \frac{1}{2} F \cdot l \cdot x^2 + c_1 \cdot x + c_2 \]
Bereich II
\[ \tag{8} E \cdot I \cdot w''_{II} = - F \cdot x + 2 \cdot F \cdot l \]
\[ \tag{9} E \cdot I \cdot w'_{II} = - \frac{1}{2} F \cdot x^2 + 2 \cdot F \cdot l \cdot x + c_3 \]
\[ \tag{10} E \cdot I \cdot w_{II} = - \frac{1}{6} F \cdot x^3 + F \cdot l \cdot x^2 + c_3 \cdot x + c_4 \]
Um die Integrationskonstanten c1 bis c4 bestimmen zu können, müssen die Rand- und Übergangsbedingungen aufgestellt werden.
Rand- und Übergangsbedingungen
wI(x=0) = 0
Die Durchbiegung an der Stelle x = 0 ist gleich Null.
\[ \require{cancel} \]\[ \tag{11} 0 = \frac{1}{E \cdot I} \left( \bcancel{\frac{1}{2}F \cdot l \cdot 0^2} + \bcancel{c_1 \cdot 0} + c_2 \right) \]
\[ \tag{12} c_2 = 0 \]
w'I(x=0) = 0
Der Winkel an der Stelle x = 0 ist gleich Null.
\[ \require{cancel} \]\[ \tag{13} 0 = \frac{1}{E \cdot I} \left(\bcancel{ F \cdot l \cdot 0} + c_1 \right) \]
\[ \tag{14} c_1 = 0 \]
wI(x=l) = wII(x=l)
Die Durchbiegung der beiden Biegelinien an der Stelle x = l ist gleich groß.
\[ \require{cancel} \]\[ \tag{15} \frac{1}{2} F \cdot l \cdot l^2 + \bcancel{c_1 \cdot l} + \bcancel{c_2} = - \frac{1}{6} F \cdot l^3 + F \cdot l \cdot l^2 + c_3 \cdot l + c_4 \]
\[ \tag{16} \frac{1}{2} F \cdot l^3 = \frac{5}{6} F \cdot l^3 + c_3 \cdot l + c_4 \]
w'I(x=l) = w'II(x=l)
Der Winkel der beiden Biegelinien an der Stelle x = l ist gleich groß.
\[ \require{cancel} \]\[ \tag{17} F \cdot l \cdot l + \bcancel{c_1} = - \frac{1}{2} F \cdot l^2 + 2 \cdot F \cdot l \cdot l + c_3 \]
Aus diesem Zusammenhang kann die Integrationskonstante c3 aufgelöst werden.
\[ \tag{18} c_3 = -\frac{1}{2}F \cdot l^2 \]
Und schlussendlich c4:
\[ \tag{19} \frac{1}{2} F \cdot l^3 = \frac{5}{6} F \cdot l^3 - \frac{1}{2}F \cdot l^3 + c_4 \]
\[ \tag{20} c_4 = \frac{1}{6}F \cdot l^3 \]
Die Gleichungen der Biegelinien lauten damit also
\[ \tag{21} w_I = \frac{1}{2 E \cdot I} F \cdot l \cdot x^2 \]
\[ \tag{22} w_{II} = \frac{F}{E \cdot I} \left( - \frac{1}{6} x^3 + l \cdot x^2 -\frac{1}{2} l^2 \cdot x + \frac{1}{6} l^3 \right) \]
Werbung




