In this exercise the bending line for a cantilevered beam with two opposite loads is calculated according to the Bernoulli beam theory.
Task
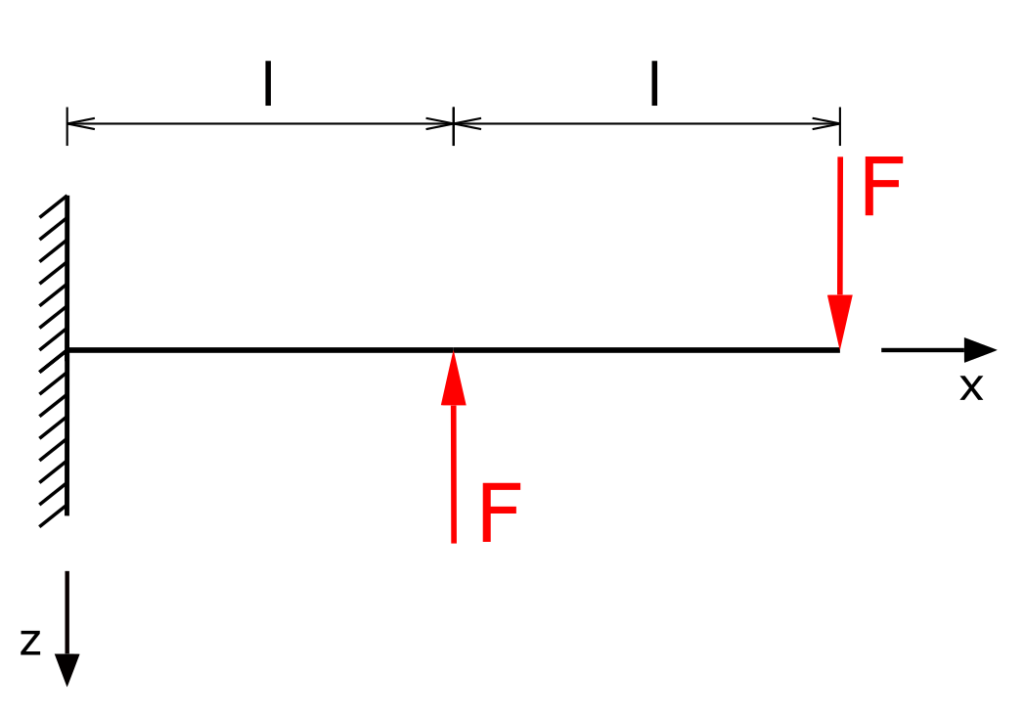
A beam fixed on one side is loaded by the opposing forces F. The bending line for the beam has to be determined!
Solution
To determine the bending line, the internal forces of the beam must be determined. Only the bending moment is relevant for the bending, i.e. in the following equations only the moment equilibria are established. The beam is divided into two sections.
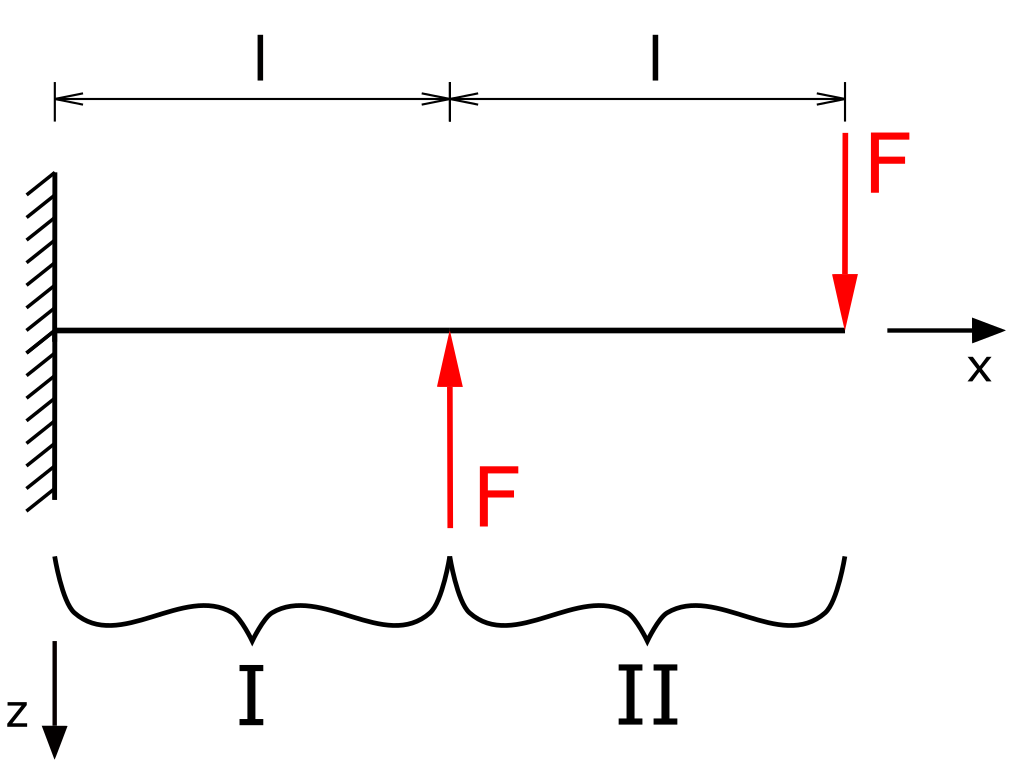
In this case, it is not necessary to determine the support reactions of the fixed restraint, so that the internal forces for section I can be started immediately.
Determination of the bending moments
Left-turning moments are positive in the following. The internal forces are applied negatively on a negative cutting edge.
Section I
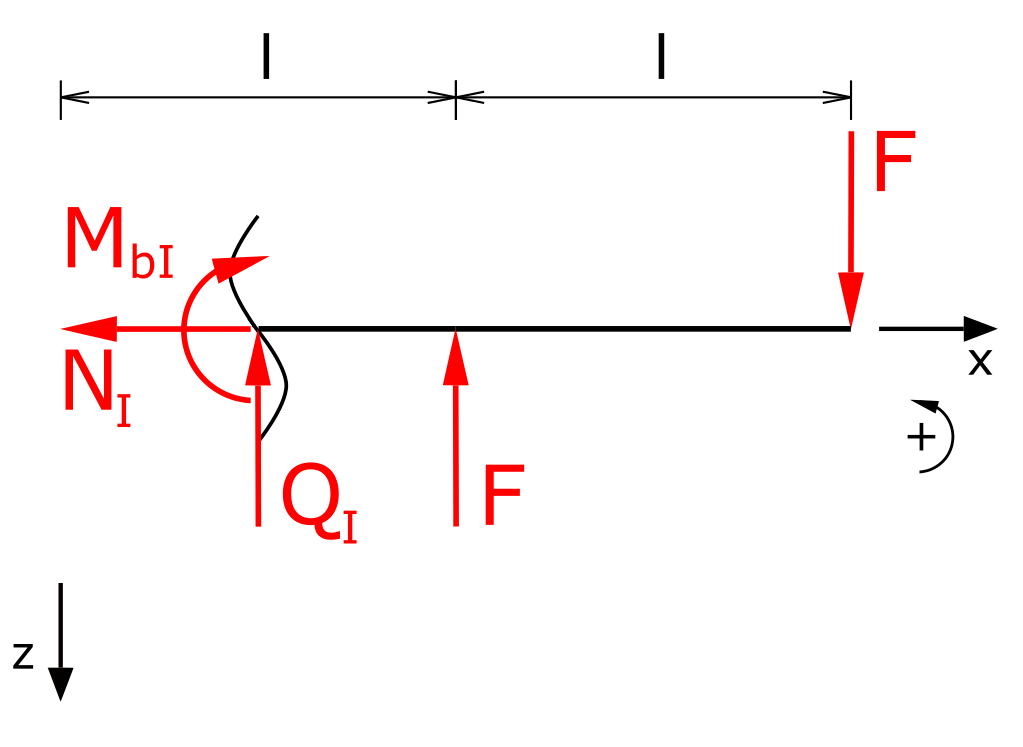
The moment balance in section I is
\[ \tag{1} \sum M(x) = 0 = -M_{bI} + F \cdot (l-x) - F \cdot (2 \cdot l -x) \]
\[ \tag{2} M_{bI} = - F \cdot l \]
Section II
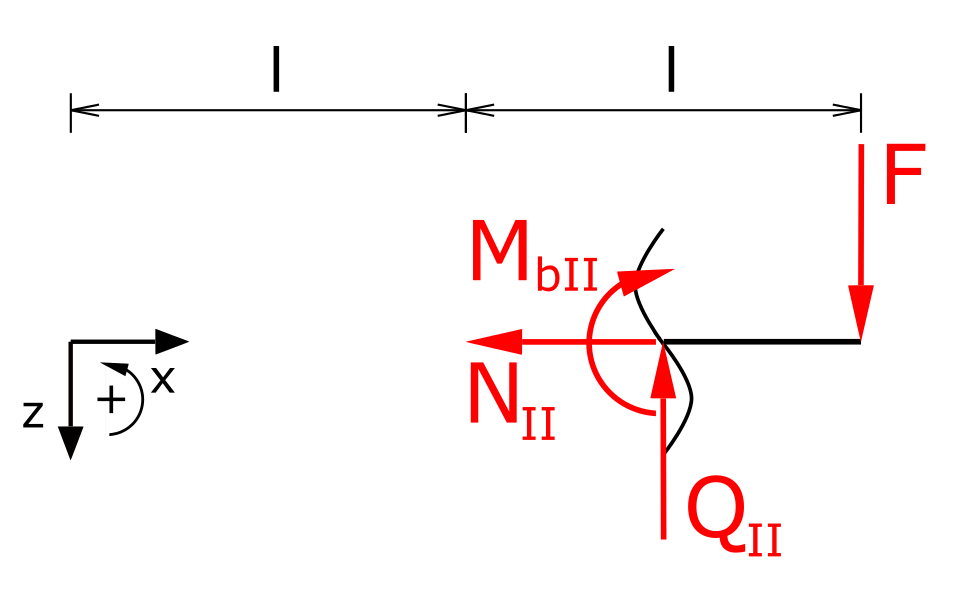
The moment balance in section II is
\[ \tag{3} \sum M(x) = 0 = -M_{bII} - F \cdot (2 \cdot l -x) \]
\[ \tag{4} M_{bI} = F \cdot x - 2 \cdot F \cdot l \]
Bending lines
The bending lines are determined on the basis of the Bernoulli beam bending. The basic relation is
\[ w'' = \frac{-M_b}{E \cdot I} \]
Here, w'' is the second derivative of the bending line, E is the Young's modulus and I is the area moment of inertia. The bending line w is obtained by double integration. It follows from this for the present case
Section I
\[ \tag{5} E \cdot I \cdot w''_I = F \cdot l \]
\[ \tag{6} E \cdot I \cdot w'_I = F \cdot l \cdot x + c_1\]
\[ \tag{7} E \cdot I \cdot w_I = \frac{1}{2} F \cdot l \cdot x^2 + c_1 \cdot x + c_2 \]
Section II
\[ \tag{8} E \cdot I \cdot w''_{II} = - F \cdot x + 2 \cdot F \cdot l \]
\[ \tag{9} E \cdot I \cdot w'_{II} = - \frac{1}{2} F \cdot x^2 + 2 \cdot F \cdot l \cdot x + c_3 \]
\[ \tag{10} E \cdot I \cdot w_{II} = - \frac{1}{6} F \cdot x^3 + F \cdot l \cdot x^2 + c_3 \cdot x + c_4 \]
In order to be able to determine the constants of integration c1 to c4, the boundary and transition conditions must be established.
Boundary and transition conditions
wI(x=0) = 0
The deflection at the point x = 0 is zero.
\[ \require{cancel} \]\[ \tag{11} 0 = \frac{1}{E \cdot I} \left( \bcancel{\frac{1}{2}F \cdot l \cdot 0^2} + \bcancel{c_1 \cdot 0} + c_2 \right) \]
\[ \tag{12} c_2 = 0 \]
w'I(x=0) = 0
The angle at the point x = 0 is equal to zero.
\[ \require{cancel} \]\[ \tag{13} 0 = \frac{1}{E \cdot I} \left(\bcancel{ F \cdot l \cdot 0} + c_1 \right) \]
\[ \tag{14} c_1 = 0 \]
wI(x=l) = wII(x=l)
The deflection of the two bending lines at the point x = l is equal.
\[ \require{cancel} \]\[ \tag{15} \frac{1}{2} F \cdot l \cdot l^2 + \bcancel{c_1 \cdot l} + \bcancel{c_2} = - \frac{1}{6} F \cdot l^3 + F \cdot l \cdot l^2 + c_3 \cdot l + c_4 \]
\[ \tag{16} \frac{1}{2} F \cdot l^3 = \frac{5}{6} F \cdot l^3 + c_3 \cdot l + c_4 \]
w'I(x=l) = w'II(x=l)
The angle of the two bending lines at the point x = l is the same.
\[ \require{cancel} \]\[ \tag{17} F \cdot l \cdot l + \bcancel{c_1} = - \frac{1}{2} F \cdot l^2 + 2 \cdot F \cdot l \cdot l + c_3 \]
From this context the integration constant c3 can be resolved.
\[ \tag{18} c_3 = -\frac{1}{2}F \cdot l^2 \]
And finally c4:
\[ \tag{19} \frac{1}{2} F \cdot l^3 = \frac{5}{6} F \cdot l^3 - \frac{1}{2}F \cdot l^3 + c_4 \]
\[ \tag{20} c_4 = \frac{1}{6}F \cdot l^3 \]
The equations of the bending lines are thus
\[ \tag{21} w_I = \frac{1}{2 E \cdot I} F \cdot l \cdot x^2 \]
\[ \tag{22} w_{II} = \frac{F}{E \cdot I} \left( - \frac{1}{6} x^3 + l \cdot x^2 -\frac{1}{2} l^2 \cdot x + \frac{1}{6} l^3 \right) \]

