Werbung
Diese Übung befasst sich mit den Lagerreaktionen bei schräger Kraft für einen Träger auf einem Fest- und einem Loslager.
Aufgabe
Eine Brücke wird durch ein bremsendes Auto durch die Kraft F, die unter dem Winkel α zur Vertikalen angreift, belastet. Welche Lagerreaktionen treten in A und B auf?
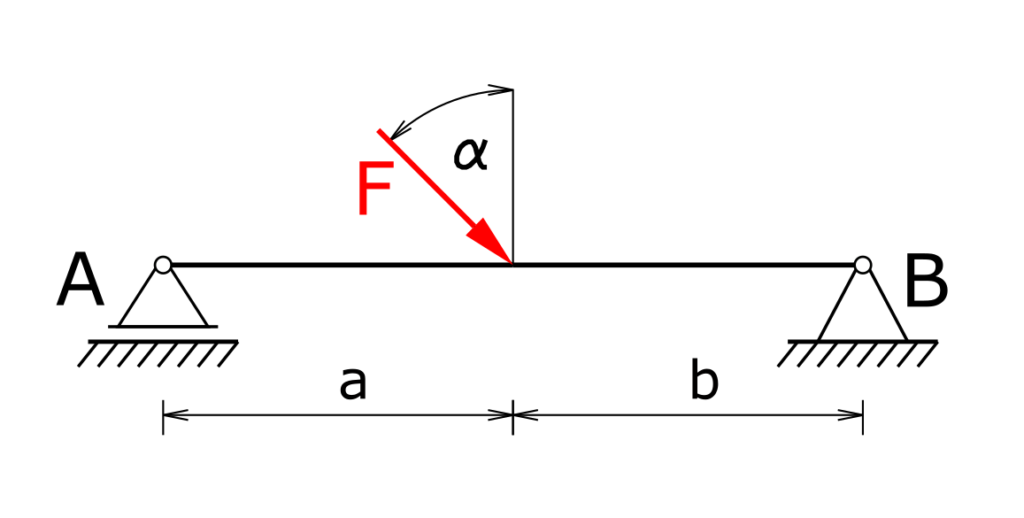
Lösung
Die schriftliche Lösung
Der Träger wird freigeschnitten und die Lagerreaktionen werden angetragen. Dabei spielt es keine Rolle, ob diese in positiver oder negativer Richtung angetragen werden. Wichtig ist jedoch, dass die in der Skizze angetragene Richtung dann auch in Kräfte- und Momentenbilanzen berücksichtigt wird, d.h. die richtigen Vorzeichen verwendet werden. Linksdrehende Momente sind positiv.
Das Loslager kann definitionsgemäß nur eine Vertikalkraft aufnehmen, d.h. die Horizontalkraft wird komplett von Lager B aufgenommen.
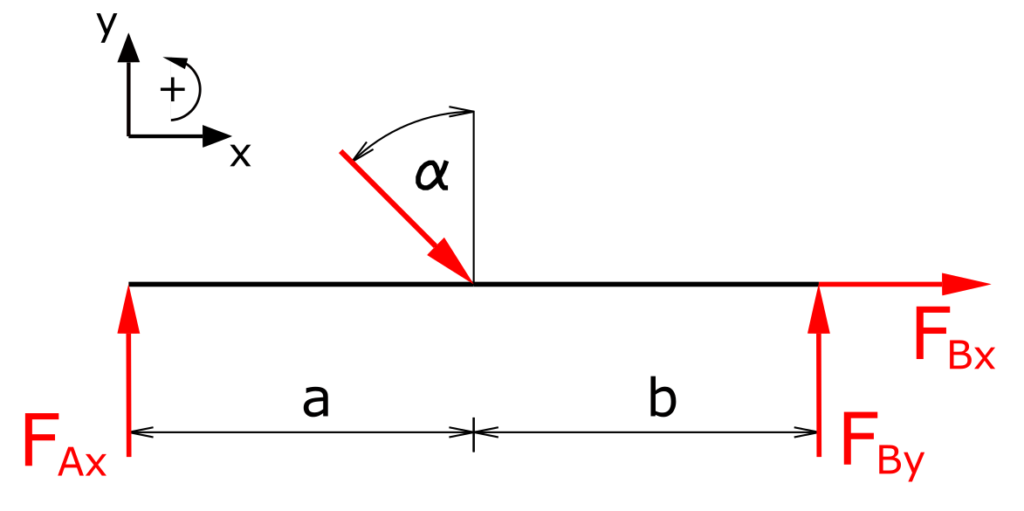
Das Kräftegleichgewicht in x-Richtung ist
\[\tag{1} \sum F_x = 0 = F \cdot \sin \alpha + F_{Bx} \]
\[\tag{2} F_{Bx} = - F \cdot \sin \alpha\]
Das Kräftegleichgewicht in y-Richtung ist
\[\tag{3} \sum F_y = 0 = F_{Ay} - F \cdot \cos \alpha + F_{By} \]
Das Momentengleichgewicht um Punkt A ist
\[\tag{4} \sum M(A) = 0 = -F \cdot \cos \alpha \cdot a + F_{By} \cdot (a+b) \]
\[\tag{5} F_{By} = \frac{F \cdot \cos \alpha \cdot a}{a+b} \]
Aus Gleichung 3 folgt
\[\tag{6} F_{Ay} = F \cdot \cos \alpha - F_{By} \]
\[\tag{7} F_{Ay} = F \cdot \cos \alpha - \frac{F \cdot \cos \alpha \cdot a}{a+b} \]
\[\tag{8} F_{Ay} = F \cdot \cos \alpha \cdot \left(1 - \frac{a}{a+b} \right) \]
Damit sind die Lagerreaktionen bei schräger Kraft ermittelt. Wenn die hier ermittelten Formeln beim Einsetzen von Zahlenwerten negative Werte ergeben, bedeutet dies, dass ihre Wirkrichtung entgegengesetzt zur skizzierten Richtung liegt. In diesem Fall ist zu erwarten, dass die Horizontalkraft für das Lager B, also FBx, genau in die andere Richtung wirkt.
Hier gibt es eine Sammlung von Aufgaben zum Thema Trägerberechnung.
Werbung




