This exercise shows how to calculate the bearing reactions under sloping load.
Task
A bridge on a floating bearing and a fixed bearing is loaded by a braking car as shown. Determine the bearing reactions in A and B!
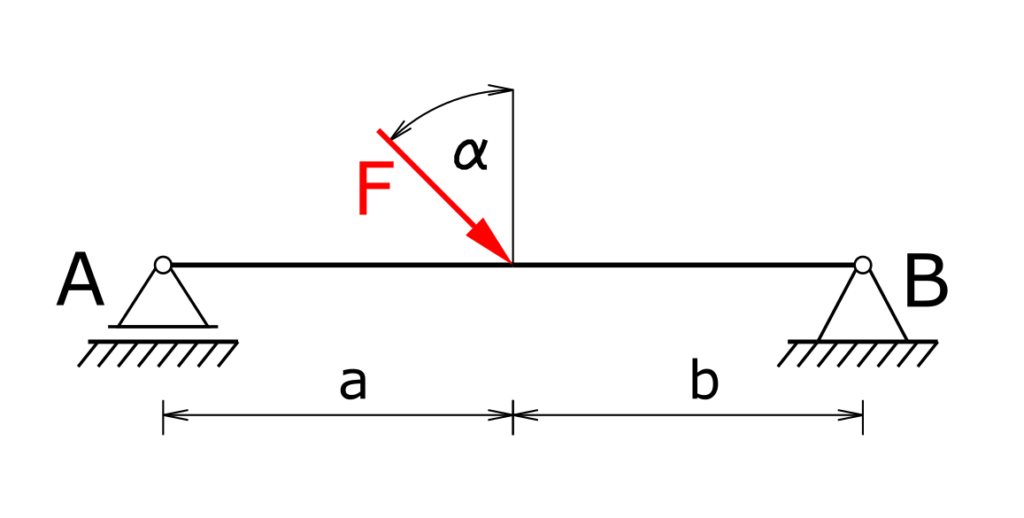
Solution
The following video is in german language. Please scroll down for the written solution.
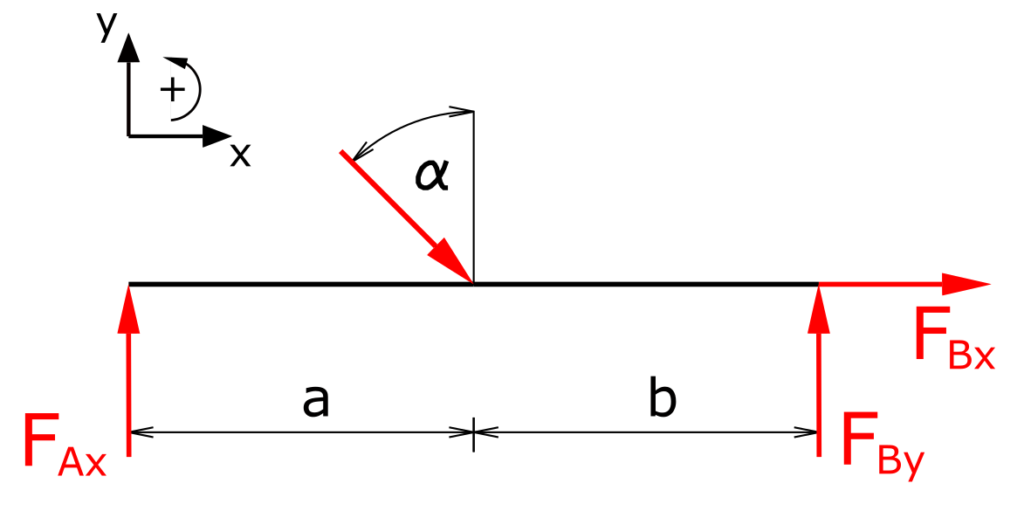
The equilibrium of forces in the x-direction is
\[\tag{1} \sum F_x = 0 = F \cdot \sin \alpha + F_{Bx} \]
\[\tag{2} F_{Bx} = - F \cdot \sin \alpha\]
The equilibrium of forces in the y-direction is
\[\tag{3} \sum F_y = 0 = F_{Ay} - F \cdot \cos \alpha + F_{By} \]
The equilibrium of moments around point A is
\[\tag{4} \sum M(A) = 0 = -F \cdot \cos \alpha \cdot a + F_{By} \cdot (a+b) \]
\[\tag{5} F_{By} = \frac{F \cdot \cos \alpha \cdot a}{a+b} \]
From equation 3 follows
\[\tag{6} F_{Ay} = F \cdot \cos \alpha - F_{By} \]
\[\tag{7} F_{Ay} = F \cdot \cos \alpha - \frac{F \cdot \cos \alpha \cdot a}{a+b} \]
\[\tag{8} F_{Ay} = F \cdot \cos \alpha \cdot \left(1 - \frac{a}{a+b} \right) \]
This was the basic exercise "bearing reactions under sloping load", used to show the appliance of fixed and floating bearings. Don't miss the other interesting exercises!

