Werbung
Aufgabe
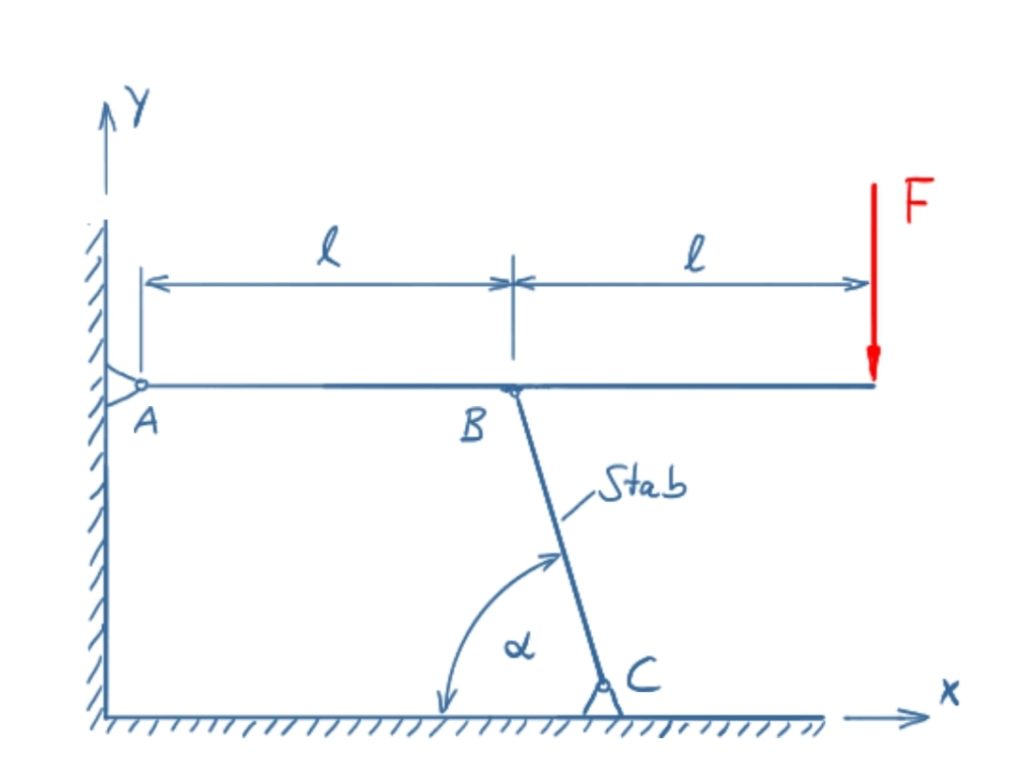
Ein Träger ist in A mit einem Festlager und in B mit einer Pendelstütze gelagert. Berechnen Sie die Lagerreaktionen in A, B und C sowie die Stabkraft.
F = 15 kNα = 75°
Lösung
Schriftliche Lösung
Es werden drei separate Abschnitte betrachtet:
\( \DeclareMathOperator{\abs}{abs} \newcommand{\ensuremath}[1]{\mbox{$#1$}} \)
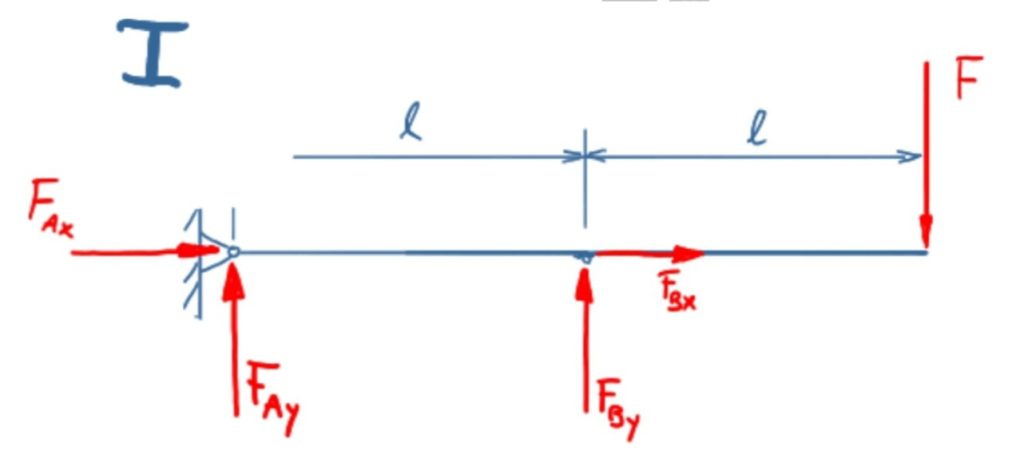
Abschnitt I: Kräftebilanz in x-Richtung
\[\tag{1} 0={F_{\mathit{Bx}}}+{F_{\mathit{Ax}}}\]
Abschnitt I: Kräftebilanz in y-Richtung
\[\tag{2} 0={F_{\mathit{By}}}+{F_{\mathit{Ay}}}-F\]
Abschnitt I: Momentenbilanz um Punkt A
\[\tag{3} 0={F_{\mathit{By}}} l-2 F l\]
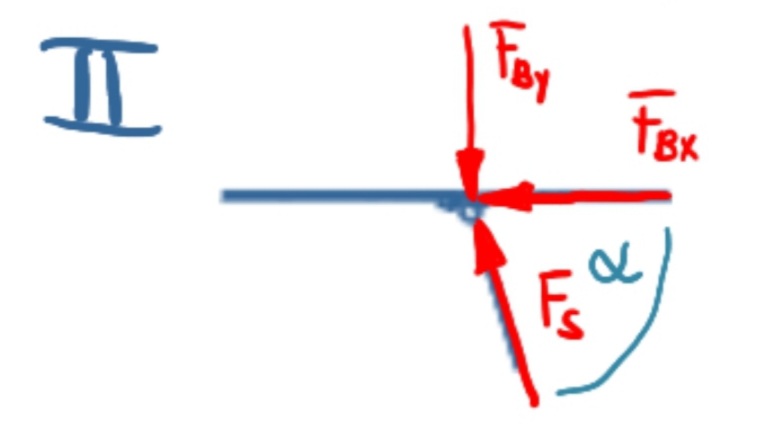
Abschnitt II: Kräftebilanz in x-Richtung
\[\tag{4} 0=-{F_S} \cos{\left( \alpha \right) }-{F_{\mathit{Bx}}}\]
Abschnitt II: Kräftebilanz in y-Richtung
\[\tag{5} 0={F_S} \sin{\left( \alpha \right) }-{F_{\mathit{By}}}\]
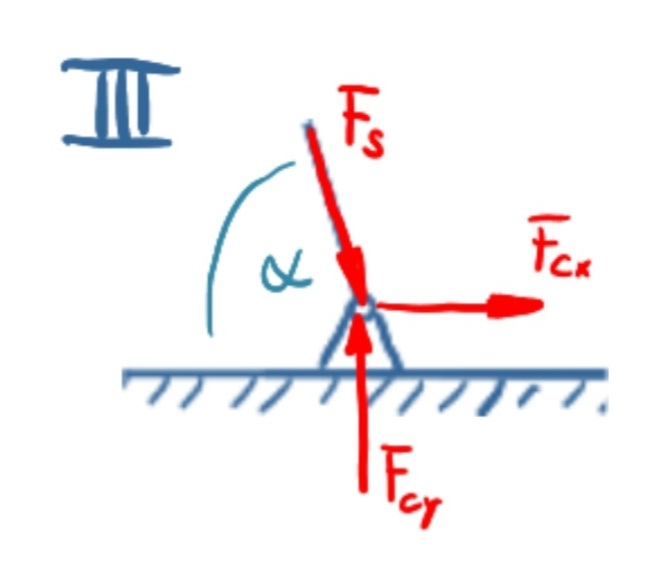
Abschnitt III: Kräftebilanz in x-Richtung
\[\tag{6} 0={F_S} \cos{\left( \alpha \right) }+{F_{\mathit{Cx}}}\]
Abschnitt III: Kräftebilanz in y-Richtung
\[\tag{7} 0={F_{\mathit{Cy}}}-{F_S} \sin{\left( \alpha \right) }\]
Nun Schritt für Schritt die oben aufgestellten Gleichungen auflösen:
\[\tag{8} {F_{\mathit{By}}}=2 F\]
\[\tag{9} {F_{\mathit{By}}}=30 \mathit{kN}\]
\[\tag{10} {F_{\mathit{Ay}}}=F-{F_{\mathit{By}}}\]
\[\tag{11} {F_{\mathit{Ay}}}=-15 \mathit{kN}\]
\[\tag{12} {F_S}=\frac{30 \mathit{kN}}{\sin{\left( \alpha \right) }}\]
\[\tag{13} {F_S}=31.06 \mathit{kN}\]
\[\tag{14} {F_{\mathit{Bx}}}=-{F_S} \cos{\left( \alpha \right) }\]
\[\tag{15} {F_{\mathit{Bx}}}=-8.04 \mathit{kN}\]
\[\tag{16} {F_{\mathit{Ax}}}=-{F_{\mathit{Bx}}}\]
\[\tag{17} {F_{\mathit{Ax}}}=8.04 \mathit{kN}\]
\[\tag{18} {F_{\mathit{Cx}}}=-{F_S} \cos{\left( \alpha \right) }\]
\[\tag{19} {F_{\mathit{Cx}}}=-8.04 \mathit{kN}\]
\[\tag{20} {F_{\mathit{Cy}}}={F_S} \sin{\left( \alpha \right) }\]
\[\tag{21} {F_{\mathit{Cy}}}=30.0 \mathit{kN}\]
Werbung




