Task
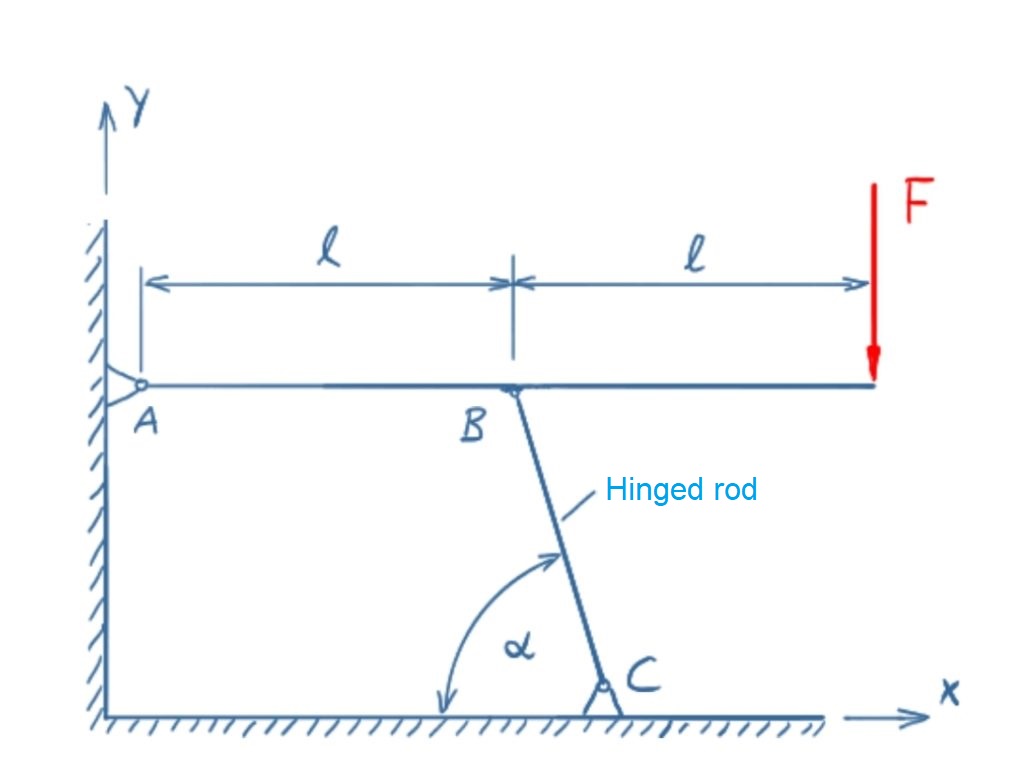
A beam is hold by a fixed bearing on the left and a hinged rod (pendulum support). The beam itself is stiff. The force F acts on the beam.
Determine the bearing loads in A, B and C and the force in the hinged rod.
F = 15 kNα = 75°
Solution
The following video is in German language, but English subtitles are available.
Step by step
The whole beam is divided into three sections to determine the reaction forces.
\( \DeclareMathOperator{\abs}{abs} \newcommand{\ensuremath}[1]{\mbox{$#1$}} \)
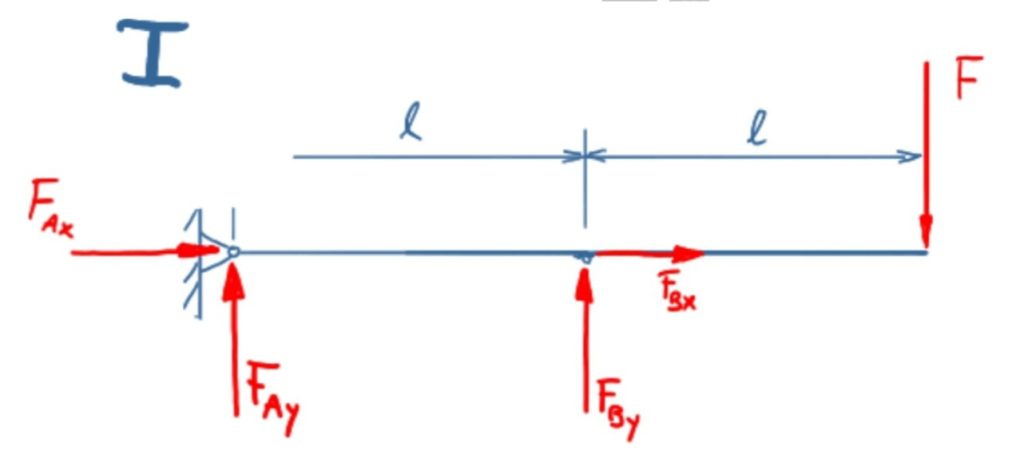
Section I: Balance of forces in x-direction
\[\tag{1} 0={F_{\mathit{Bx}}}+{F_{\mathit{Ax}}}\]
Section I: Balance of forces in y-direction
\[\tag{2} 0={F_{\mathit{By}}}+{F_{\mathit{Ay}}}-F\]
Section I: Balance of moments around A
\[\tag{3} 0={F_{\mathit{By}}} l-2 F l\]
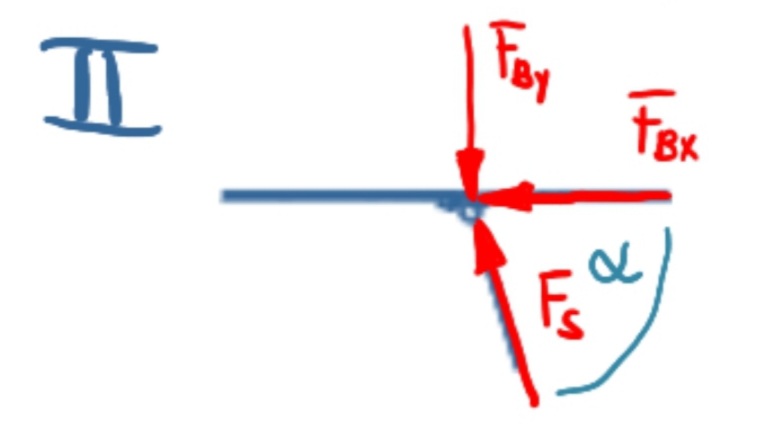
Section II: Balance of forces in x-direction
\[\tag{4} 0=-{F_S} \cos{\left( \alpha \right) }-{F_{\mathit{Bx}}}\]
Section II: Balance of forces in y-direction
\[\tag{5} 0={F_S} \sin{\left( \alpha \right) }-{F_{\mathit{By}}}\]
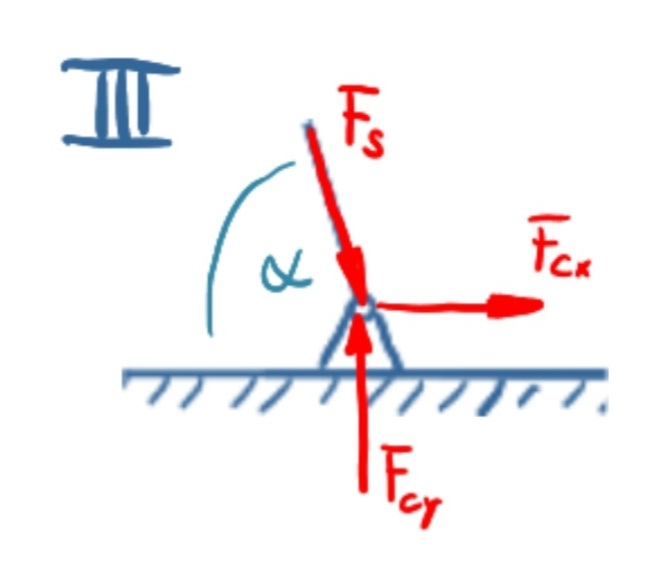
Section III: Balance of forces in x-direction
\[\tag{6} 0={F_S} \cos{\left( \alpha \right) }+{F_{\mathit{Cx}}}\]
Section III: Balance of forces in y-direction
\[\tag{7} 0={F_{\mathit{Cy}}}-{F_S} \sin{\left( \alpha \right) }\]
Step by step solution of the found equations
\[\tag{8} {F_{\mathit{By}}}=2 F\]
\[\tag{9} {F_{\mathit{By}}}=30 \mathit{kN}\]
\[\tag{10} {F_{\mathit{Ay}}}=F-{F_{\mathit{By}}}\]
\[\tag{11} {F_{\mathit{Ay}}}=-15 \mathit{kN}\]
\[\tag{12} {F_S}=\frac{30 \mathit{kN}}{\sin{\left( \alpha \right) }}\]
\[\tag{13} {F_S}=31.06 \mathit{kN}\]
\[\tag{14} {F_{\mathit{Bx}}}=-{F_S} \cos{\left( \alpha \right) }\]
\[\tag{15} {F_{\mathit{Bx}}}=-8.04 \mathit{kN}\]
\[\tag{16} {F_{\mathit{Ax}}}=-{F_{\mathit{Bx}}}\]
\[\tag{17} {F_{\mathit{Ax}}}=8.04 \mathit{kN}\]
\[\tag{18} {F_{\mathit{Cx}}}=-{F_S} \cos{\left( \alpha \right) }\]
\[\tag{19} {F_{\mathit{Cx}}}=-8.04 \mathit{kN}\]
\[\tag{20} {F_{\mathit{Cy}}}={F_S} \sin{\left( \alpha \right) }\]
\[\tag{21} {F_{\mathit{Cy}}}=30.0 \mathit{kN}\]

