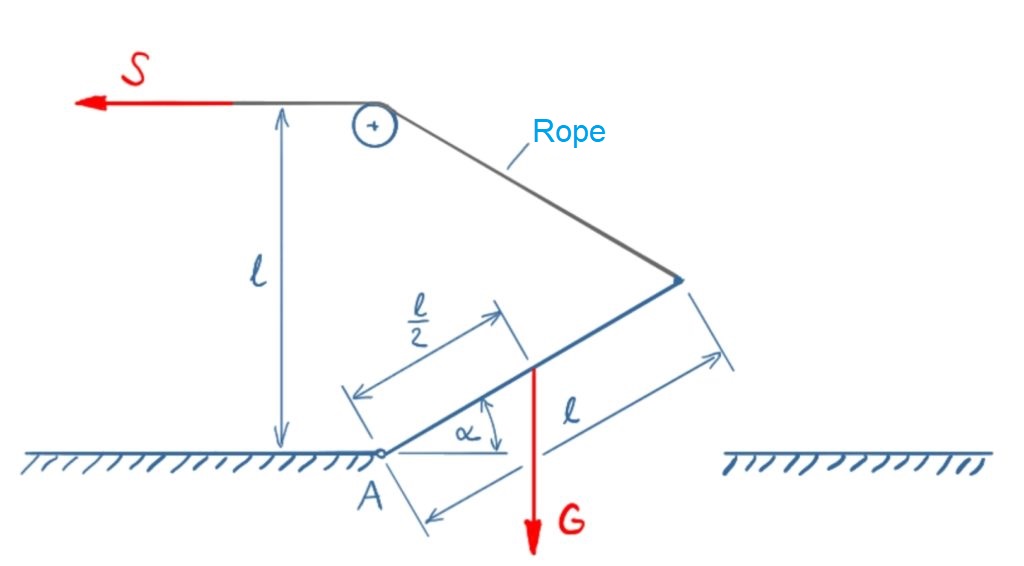
Task
A bascule bridge with its own weight G is held by a rope. The rope is deflected by a pulley. The dimensions of the pulley don't have to be considered.
Determine the function of the rope force depending on the opening angle of the bascule bridge!
When does rope force become obsolete?
Solution
The following video is in german language, but English subtitles are available.
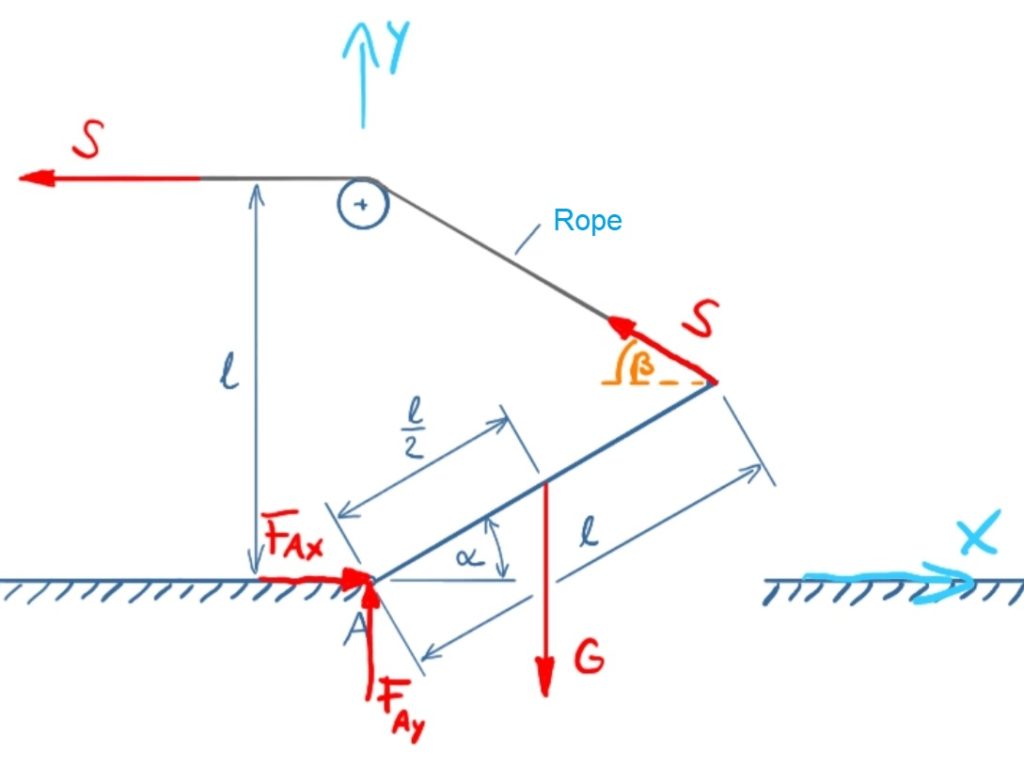
To consider the rope force in the balances of moments and forces in a comfortable way, we introduce the angle β. This results in:
\[ \tag{1} \sum F_x = 0 = F_{Ax} - S \cdot \cos \beta \]
\[ \tag{2} \sum F_y = 0 = F_{Ay} - G + S \cdot \sin \beta \]
S can be determined from the balance of moments. We choose A as pivot point
\[ \tag{3} \sum M(A) = 0 = -G \cdot \frac{l}{2} \cdot \cos \alpha + S \cdot l \cdot \cos \beta \cdot \sin \alpha + S \cdot l \cdot \sin \beta \cdot \cos \alpha \]
\[ \tag{4} G \cdot \frac{\bcancel{l}}{2} \cdot \cos \alpha = S \cdot \bcancel{l} \cdot \left( \cos \beta \cdot \sin \alpha + \sin \beta \cdot \cos \alpha \right) \]
\[ \tag{5} S = \frac{G \cdot \cos \alpha}{2 \cdot \left( \cos \beta \cdot \sin \alpha + \sin \beta \cdot \cos \alpha \right) } \]
The trigonometric functions with α and β can be simplified, so the following function results:
\[ \tag{6} S = \frac{G \cdot \cos \alpha}{2 \cdot \sin \left( \alpha + \beta \right) } \]
The angle β can be described this:
\[ \tag{7} \beta = arctan \left( \frac{\bcancel{l}1 - \bcancel{l} \cdot \sin \alpha}{\bcancel{l} \cdot \cos \alpha} \right) \]
The wanted function S(α) is:
\[ \tag{8} S(\alpha) = \frac{G \cdot \cos \alpha}{2 \cdot \sin \left( \alpha + arctan \left( \frac{1 - \sin \alpha}{\cos \alpha} \right) \right) } \]
When does the rope force become obsolete?
The function S(α) returns Zero if the counter returns Zero. This happens if the angle α is 90°. So the rope force becomes obsolete at an angle of α = 90°.

