Task
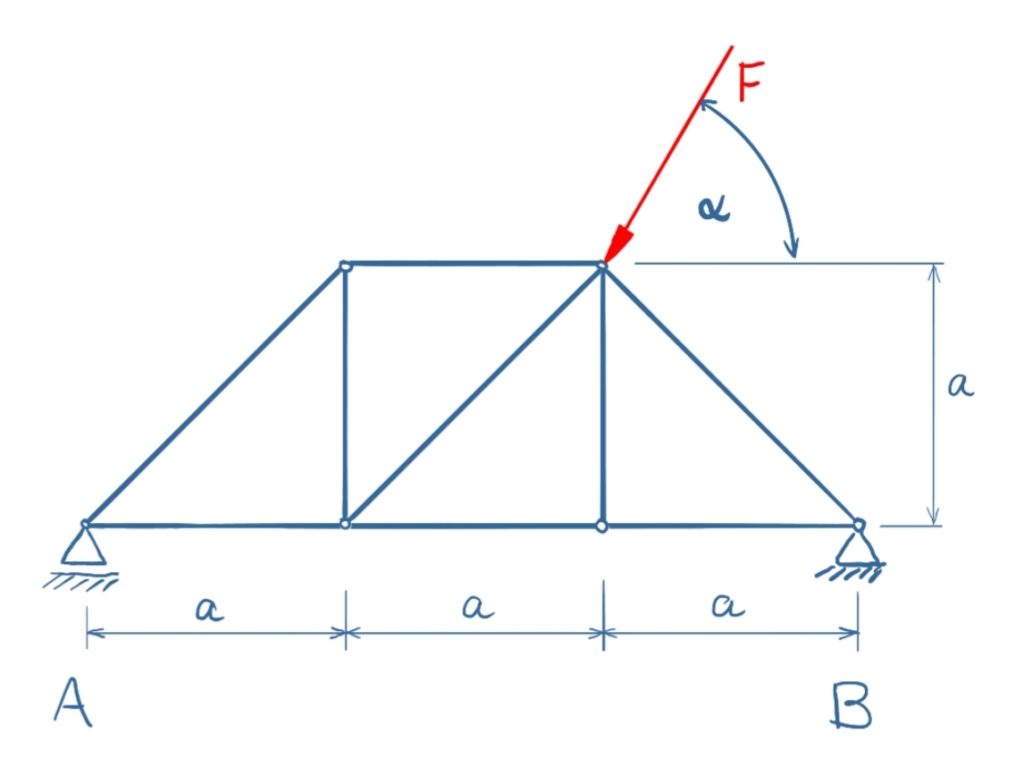
The force F is acting under an angle on a truss. The truss has a locating bearing and a floating bearing. Calculate the bearing loads and the member forces for the truss.
F = 10 kNα = 60°
a = 2 m
Solution
The following video is in german language.
Sketches
The following sketches show the bearing reaction forces, the member and node numbering and the location and direction of the forces at each node.
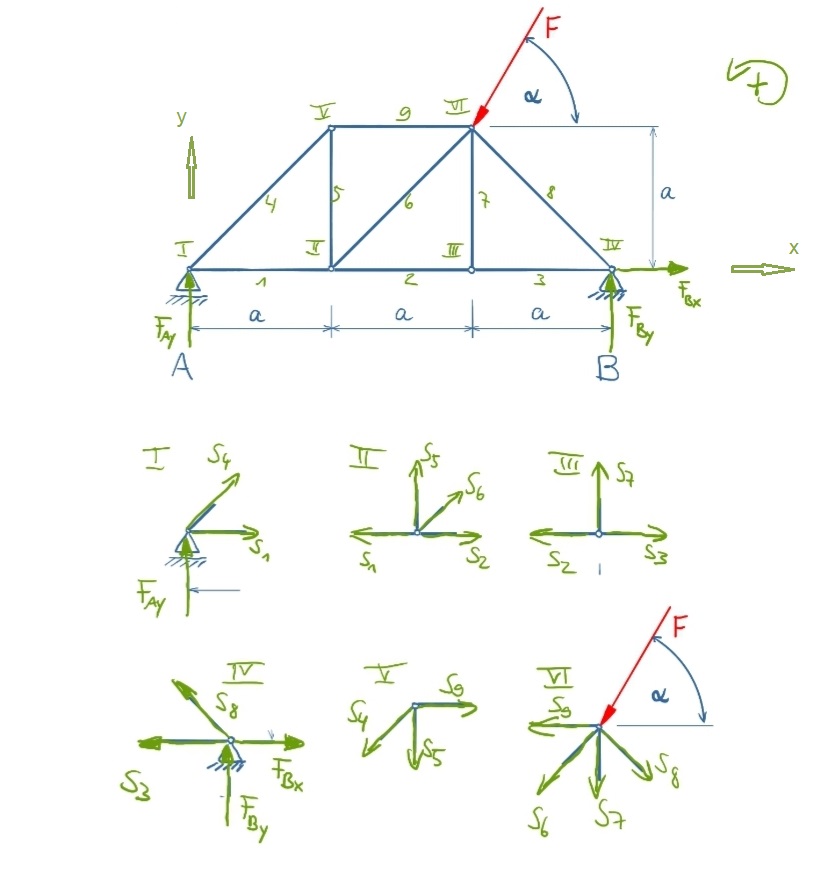
The forces are solved symbolic first, then the real numbers are set in to calculate the values. Since the angles of the bars are always 45 °, the alternative notation of the trigonometric functions is used.
\( \DeclareMathOperator{\abs}{abs} \newcommand{\ensuremath}[1]{\mbox{$#1$}} \)
\[\tag{1} 0=-F \sin{\left( \alpha \right) }+{F_{\mathit{By}}}+{F_{\mathit{Ay}}}\]
\[\tag{2} 0={F_{\mathit{Bx}}}-F \cos{\left( \alpha \right) }\]
\[\tag{3} 0=-2 F a \sin{\left( \alpha \right) }+F a \cos{\left( \alpha \right) }+3 {F_{\mathit{By}}} a\]
Node equations
\[\tag{4} 0=\frac{{S_4}}{\sqrt{2}}+{S_1}\]
\[\tag{5} 0=\frac{{S_4}}{\sqrt{2}}+{F_{\mathit{Ay}}}\]
\[\tag{6} 0=\frac{{S_6}}{\sqrt{2}}+{S_2}-{S_1}\]
\[\tag{7} 0=\frac{\mathit{S6}}{\sqrt{2}}+\mathit{S5}\]
\[\tag{8} 0={S_3}-{S_2}\]
\[\tag{9} 0={S_7}\]
\[\tag{10} 0=-\frac{{S_8}}{\sqrt{2}}-{S_3}+{F_{\mathit{Bx}}}\]
\[\tag{11} 0=\frac{{S_8}}{\sqrt{2}}+{F_{\mathit{By}}}\]
\[\tag{12} 0={S_9}-\frac{{S_4}}{\sqrt{2}}\]
\[\tag{13} 0=-{S_5}-\frac{{S_4}}{\sqrt{2}}\]
\[\tag{14} 0=-F \cos{\left( \alpha \right) }-{S_9}+\frac{{S_8}}{\sqrt{2}}-\frac{{S_6}}{\sqrt{2}}\]
\[\tag{15} 0=-F \sin{\left( \alpha \right) }-\frac{{S_8}}{\sqrt{2}}-{S_7}-\frac{{S_6}}{\sqrt{2}}\]
\[\tag{16} {F_{\mathit{Bx}}}=F \cos{\left( \alpha \right) }\]
\[\tag{17} {S_7}=0\]
\[\tag{18} {F_{\mathit{By}}}=\frac{2 F \sin{\left( \alpha \right) }-F \cos{\left( \alpha \right) }}{3}\]
\[\tag{19} 0=\frac{2 F \sin{\left( \alpha \right) }-F \cos{\left( \alpha \right) }}{3}-F \sin{\left( \alpha \right) }+{F_{\mathit{Ay}}}\]
\[\tag{20} {F_{\mathit{Ay}}}=\frac{F \sin{\left( \alpha \right) }+F \cos{\left( \alpha \right) }}{3}\]
\[\tag{21} {S_4}=-\frac{\sqrt{2} F \sin{\left( \alpha \right) }+\sqrt{2} F \cos{\left( \alpha \right) }}{3}\]
\[\tag{22} {S_1}=\frac{F \sin{\left( \alpha \right) }+F \cos{\left( \alpha \right) }}{3}\]
\[\tag{23} {S_9}=-\frac{F \sin{\left( \alpha \right) }+F \cos{\left( \alpha \right) }}{3}\]
\[\tag{24} {S_5}=\frac{F \sin{\left( \alpha \right) }+F \cos{\left( \alpha \right) }}{3}\]
\[\tag{25} {S_8}=-\frac{{{2}^{\frac{3}{2}}} F \sin{\left( \alpha \right) }-\sqrt{2} F \cos{\left( \alpha \right) }}{3}\]
\[\tag{26} {S_3}=\frac{2 F \sin{\left( \alpha \right) }+2 F \cos{\left( \alpha \right) }}{3}\]
\[\tag{27} {S_6}=-\frac{\sqrt{2} F \sin{\left( \alpha \right) }+\sqrt{2} F \cos{\left( \alpha \right) }}{3}\]
\[\tag{28} {S_2}=\frac{2 F \sin{\left( \alpha \right) }+2 F \cos{\left( \alpha \right) }}{3}\]
\[\tag{29} {S_1}=4.55 \mathit{kN}\]
\[\tag{30} {S_2}=9.11 \mathit{kN}\]
\[\tag{31} {S_3}=9.11 \mathit{kN}\]
\[\tag{32} {S_4}=-6.44 \mathit{kN}\]
\[\tag{33} {S_5}=4.55 \mathit{kN}\]
\[\tag{34} {S_6}=-6.44 \mathit{kN}\]
\[\tag{35} {S_7}=0.0\]
\[\tag{36} {S_8}=-5.81 \mathit{kN}\]
\[\tag{37} {S_9}=-4.55 \mathit{kN}\]
\[\tag{38} {F_{\mathit{Ay}}}=4.55 \mathit{kN}\]
\[\tag{39} {F_{\mathit{By}}}=4.11 \mathit{kN}\]
\[\tag{40} {F_{\mathit{Bx}}}=5.0 \mathit{kN}\]


Bearing reactions