Werbung
In dieser Übung wird gezeigt, wie man die Stabkräfte eines Stabwerks mit dem Knotenpunktverfahren berechnen kann. Ein FEM-Tool zur Berechnung von Stabwerken ist hier zu finden.
Aufgabe
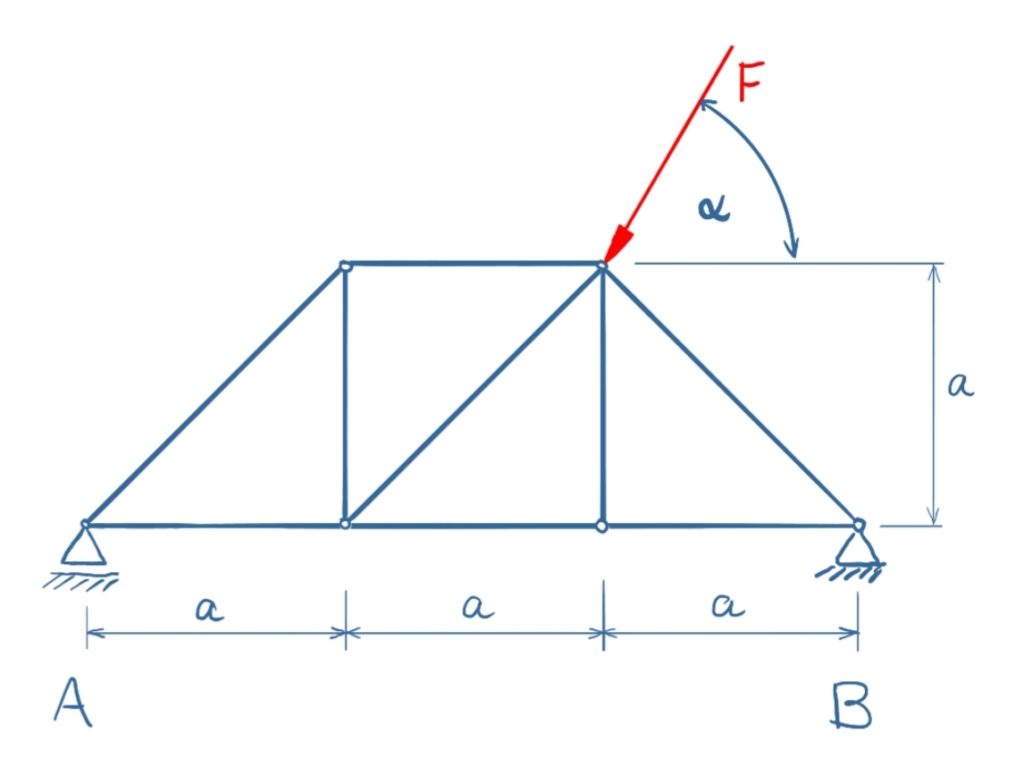
Berechnen Sie für die Lagerreaktionen und Stabkräfte für das abgebildete Stabwerk.
F = 10 kNα = 60°
a = 2 m
Lösung
Lösungsvideo
Schriftliche Lösung
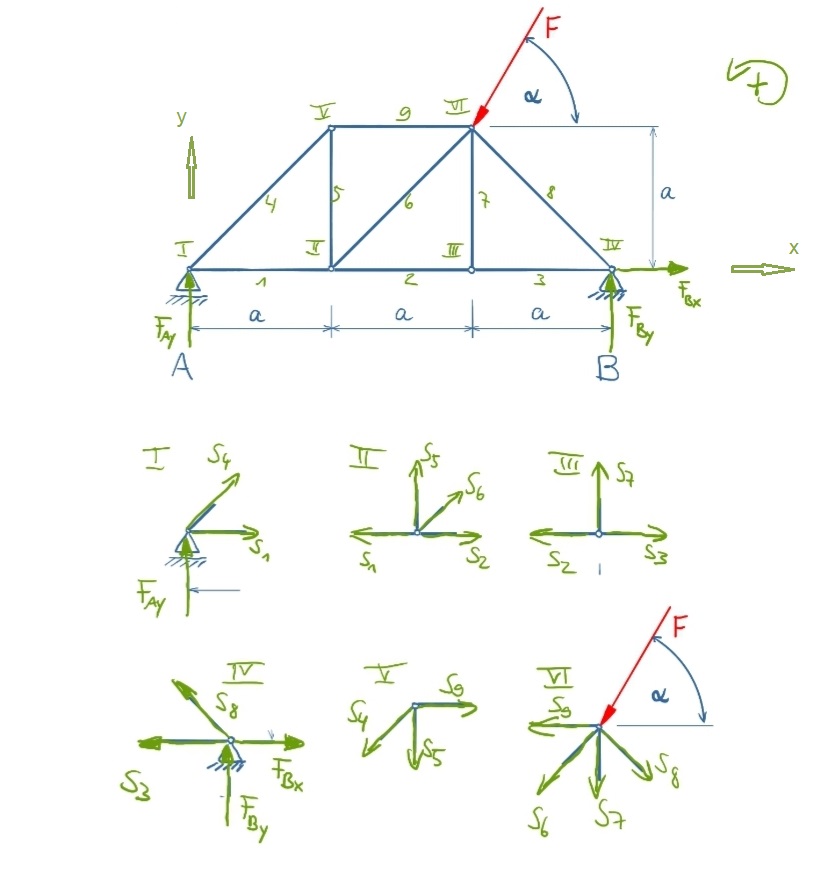
In den nachfolgenden Funktionen für die Stabkräfte werden die Winkelfunktionen nicht weiter aufgeführt, da aufgrund der geometrischen Anordnung (alle Stäbe haben einen Winkel von 45°) die bereits berechneten Ergebnisse der Winkelfunktionen in kurzer Schreibweise eingesetzt werden können.
\( \DeclareMathOperator{\abs}{abs} \newcommand{\ensuremath}[1]{\mbox{$#1$}} \)
Lagerreaktionen
Summe aller Kräfte in y-Richtung
\[\tag{1} 0=-F \sin{\left( \alpha \right) }+{F_{\mathit{By}}}+{F_{\mathit{Ay}}}\]
Summe aller Kräfte in x-Richtung
\[\tag{2} 0={F_{\mathit{Bx}}}-F \cos{\left( \alpha \right) }\]
Summe aller Momente um A
\[\tag{3} 0=-2 F a \sin{\left( \alpha \right) }+F a \cos{\left( \alpha \right) }+3 {F_{\mathit{By}}} a\]
Knoten I x
\[\tag{4} 0=\frac{{S_4}}{\sqrt{2}}+{S_1}\]
Knoten I y
\[\tag{5} 0=\frac{{S_4}}{\sqrt{2}}+{F_{\mathit{Ay}}}\]
Knoten II x
\[\tag{6} 0=\frac{{S_6}}{\sqrt{2}}+{S_2}-{S_1}\]
Knoten II y
\[\tag{7} 0=\frac{\mathit{S6}}{\sqrt{2}}+\mathit{S5}\]
Knoten III x
\[\tag{8} 0={S_3}-{S_2}\]
Knoten III y
\[\tag{9} 0={S_7}\]
\[\tag{10} 0=-\frac{{S_8}}{\sqrt{2}}-{S_3}+{F_{\mathit{Bx}}}\]
Knoten IV y
\[\tag{11} 0=\frac{{S_8}}{\sqrt{2}}+{F_{\mathit{By}}}\]
Knoten V x
\[\tag{12} 0={S_9}-\frac{{S_4}}{\sqrt{2}}\]
Knoten V y
\[\tag{13} 0=-{S_5}-\frac{{S_4}}{\sqrt{2}}\]
Knoten VI x
\[\tag{14} 0=-F \cos{\left( \alpha \right) }-{S_9}+\frac{{S_8}}{\sqrt{2}}-\frac{{S_6}}{\sqrt{2}}\]
Knoten VI y
\[\tag{15} 0=-F \sin{\left( \alpha \right) }-\frac{{S_8}}{\sqrt{2}}-{S_7}-\frac{{S_6}}{\sqrt{2}}\]
Gleichung (2) nach FBx auflösen
\[\tag{16} {F_{\mathit{Bx}}}=F \cos{\left( \alpha \right) }\]
Gleichung (9) liefert den Nullstab S7
\[\tag{17} {S_7}=0\]
Gleichung (3) nach FBy auflösen
\[\tag{18} {F_{\mathit{By}}}=\frac{2 F \sin{\left( \alpha \right) }-F \cos{\left( \alpha \right) }}{3}\]
FBy in Gleichung (1) einsetzen ...
\[\tag{19} 0=\frac{2 F \sin{\left( \alpha \right) }-F \cos{\left( \alpha \right) }}{3}-F \sin{\left( \alpha \right) }+{F_{\mathit{Ay}}}\]
... und nach FAy auflösen
\[\tag{20} {F_{\mathit{Ay}}}=\frac{F \sin{\left( \alpha \right) }+F \cos{\left( \alpha \right) }}{3}\]
Im Folgenden werden die bisher gelösten Kräfte in die verbleibenden Gleichungen eingesetzt und die Unbekannten aufgelöst
\[\tag{21} {S_4}=-\frac{\sqrt{2} F \sin{\left( \alpha \right) }+\sqrt{2} F \cos{\left( \alpha \right) }}{3}\]
\[\tag{22} {S_1}=\frac{F \sin{\left( \alpha \right) }+F \cos{\left( \alpha \right) }}{3}\]
\[\tag{23} {S_9}=-\frac{F \sin{\left( \alpha \right) }+F \cos{\left( \alpha \right) }}{3}\]
\[\tag{24} {S_5}=\frac{F \sin{\left( \alpha \right) }+F \cos{\left( \alpha \right) }}{3}\]
\[\tag{25} {S_8}=-\frac{{{2}^{\frac{3}{2}}} F \sin{\left( \alpha \right) }-\sqrt{2} F \cos{\left( \alpha \right) }}{3}\]
\[\tag{26} {S_3}=\frac{2 F \sin{\left( \alpha \right) }+2 F \cos{\left( \alpha \right) }}{3}\]
\[\tag{27} {S_6}=-\frac{\sqrt{2} F \sin{\left( \alpha \right) }+\sqrt{2} F \cos{\left( \alpha \right) }}{3}\]
\[\tag{28} {S_2}=\frac{2 F \sin{\left( \alpha \right) }+2 F \cos{\left( \alpha \right) }}{3}\]
Resultierende Stabkräfte und Lagerreaktionen
\[\tag{29} {S_1}=4.55 \mathit{kN}\]
\[\tag{30} {S_2}=9.11 \mathit{kN}\]
\[\tag{31} {S_3}=9.11 \mathit{kN}\]
\[\tag{32} {S_4}=-6.44 \mathit{kN}\]
\[\tag{33} {S_5}=4.55 \mathit{kN}\]
\[\tag{34} {S_6}=-6.44 \mathit{kN}\]
\[\tag{35} {S_7}=0.0\]
\[\tag{36} {S_8}=-5.81 \mathit{kN}\]
\[\tag{37} {S_9}=-4.55 \mathit{kN}\]
\[\tag{38} {F_{\mathit{Ay}}}=4.55 \mathit{kN}\]
\[\tag{39} {F_{\mathit{By}}}=4.11 \mathit{kN}\]
\[\tag{40} {F_{\mathit{Bx}}}=5.0 \mathit{kN}\]
Werbung




