This exercise is about the following questions:
- How to calculate the forces in a joint?
- How to calculate the bearing loads if a force acts with an offset?
Task
A force F acts with an offset on a beam. The beam is fixed on one side and connected to a floating bearing with a joint. Find the reaction forces in A, B and C.
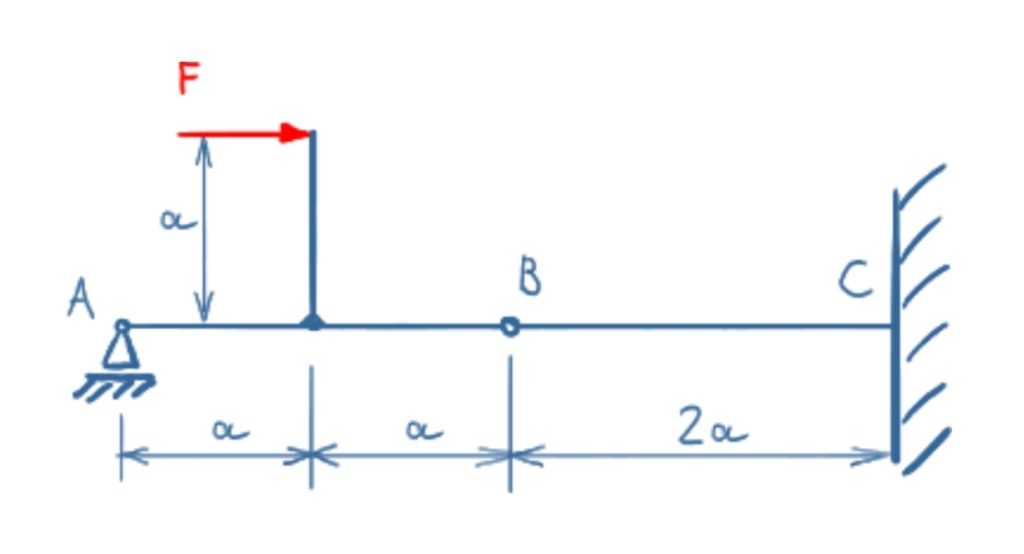
Solution
The following video is in german language.
The beam is divided into two sections to determine the bearing reactions and the joint forces.
Section 1
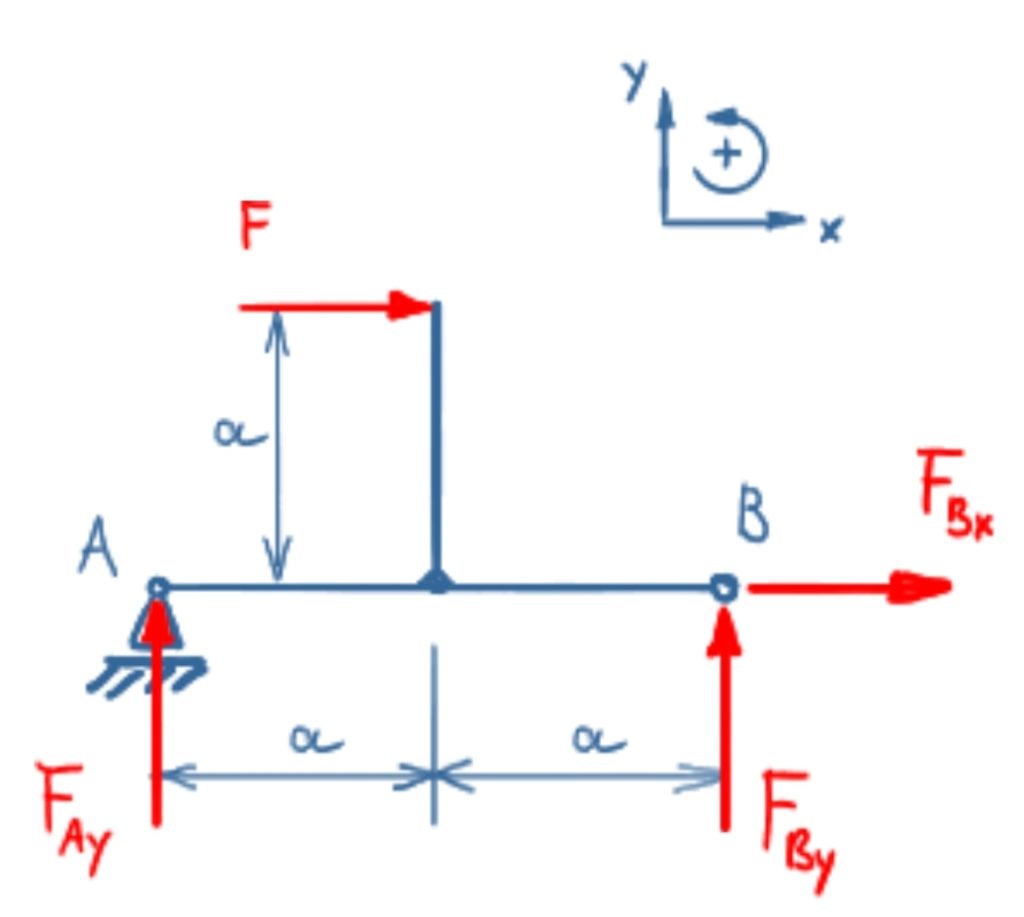
The equilibrium of forces in the x-direction is
\[\tag{1} \sum F_x = 0 = F + F_{Bx} \]
\[\tag{2} F_{Bx} = -F \]
The equilibrium of forces in the y-direction is
\[\tag{3} \sum F_y = 0 = F_{Ay} + F_{By} \]
The equilibrium of moments around point A gives
\[\tag{4} \sum M(A) = 0 = -F \cdot a + F_{By} \cdot 2 \cdot a \]
\[\tag{5} F_{By} = \frac{F \cdot \bcancel{a}}{2 \cdot \bcancel{a}} \]
So the result from equation 3 is
\[\tag{6} F_{Ay} = - \frac{F}{2} \]
Section 2
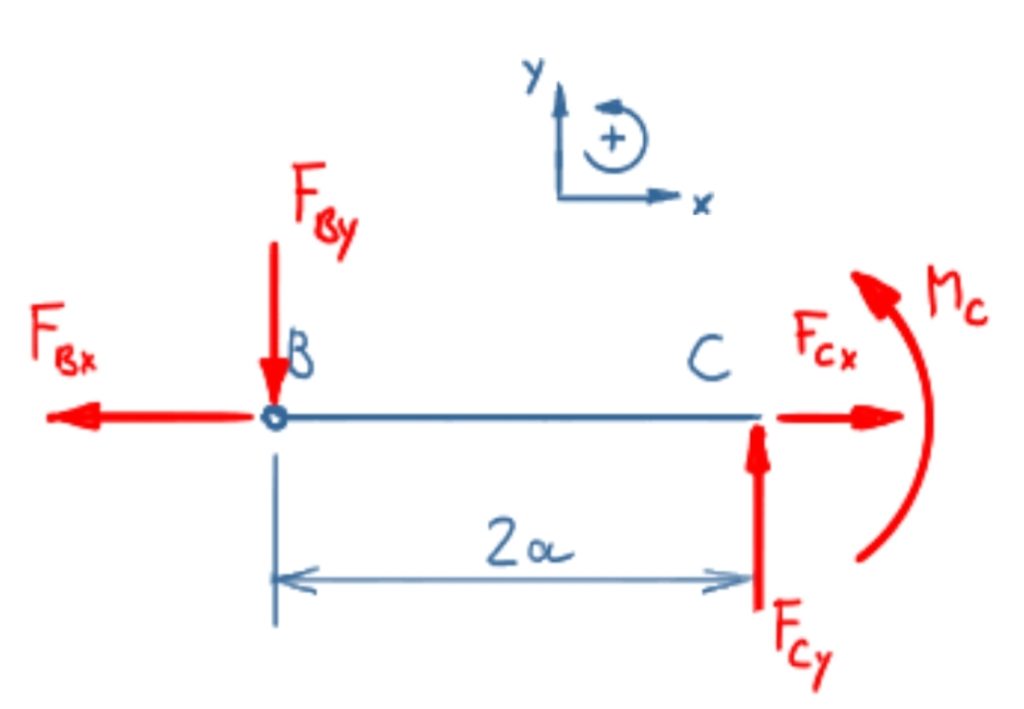
The equilibrium of forces in the x-direction is
\[\tag{7} \sum F_x = 0 = - F_{Bx} + F_{Cx} \]
\[\tag{8} F_{Cx} = -F \]
The equilibrium of forces in the y-direction is
\[\tag{9} \sum F_y = 0 = - F_{By} + F_{Cy} \]
\[\tag{10} F_{Cy} = \frac{F}{2} \]
The equilibrium of moments around point C gives
\[\tag{11} \sum M(C) = 0 = F_{By} \cdot 2a + M_C \]
\[\tag{12} M_C = - F \cdot a \]

