Werbung
Diese Aufgabe beschäftigt sich mit folgenden Fragen:
- Wie berechnet man Gelenkkräfte?
- Wie berechne ich einen Rahmen mit zwei Festlagern?
- Welche unterschiedlichen Lösungsansätze zur Berechnung von Gelenkkräften gibt es?
Aufgabe
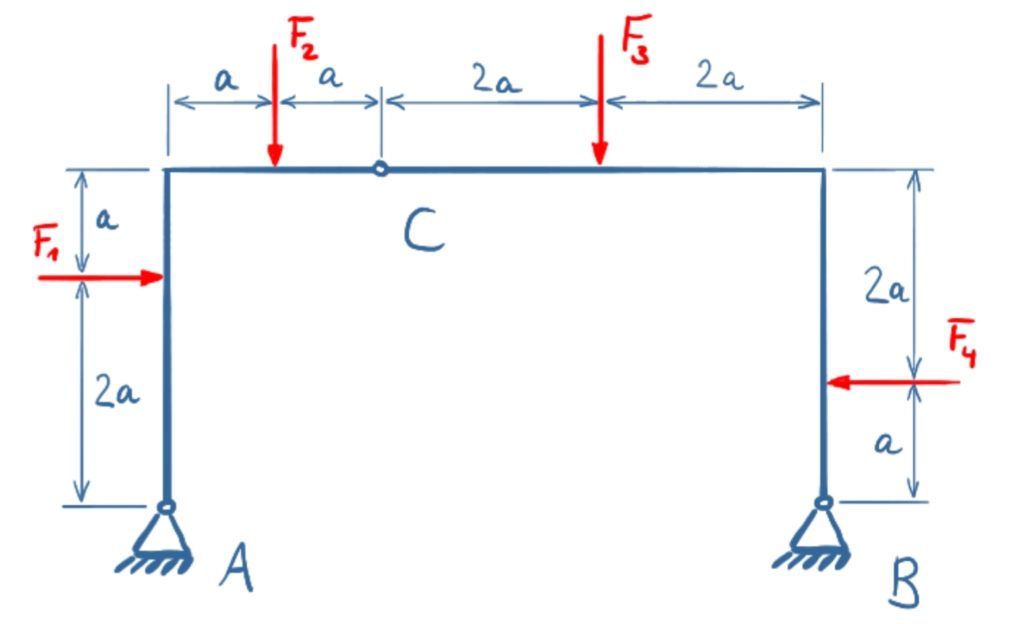
Auf das abgebildete Ständerwerk mit zwei Festlagern wirken die Kräfte F1 bis F4. Wie groß sind die Lagerreaktionen und die Kräfte in Gelenk C?
F1 = F4 = 10 kN, F2 = 30 kN, F3 = 60 kN, a = 1 m
Lösung
Die Lösung kann auf unterschiedliche Weise erfolgen, hier werden zwei Varianten gezeigt:
Lösung Variante 1 betrachtet von Beginn an beide Bereiche links und rechts des Gelenks separat und stellt die entsprechenden Gleichungen auf.
Lösung Variante 2 stellt als ersten Schritt die Gleichgewichtsbedingungen für das Gesamtsystem auf, und löst dann die Kräfte der Teilbereiche.
Variante 1
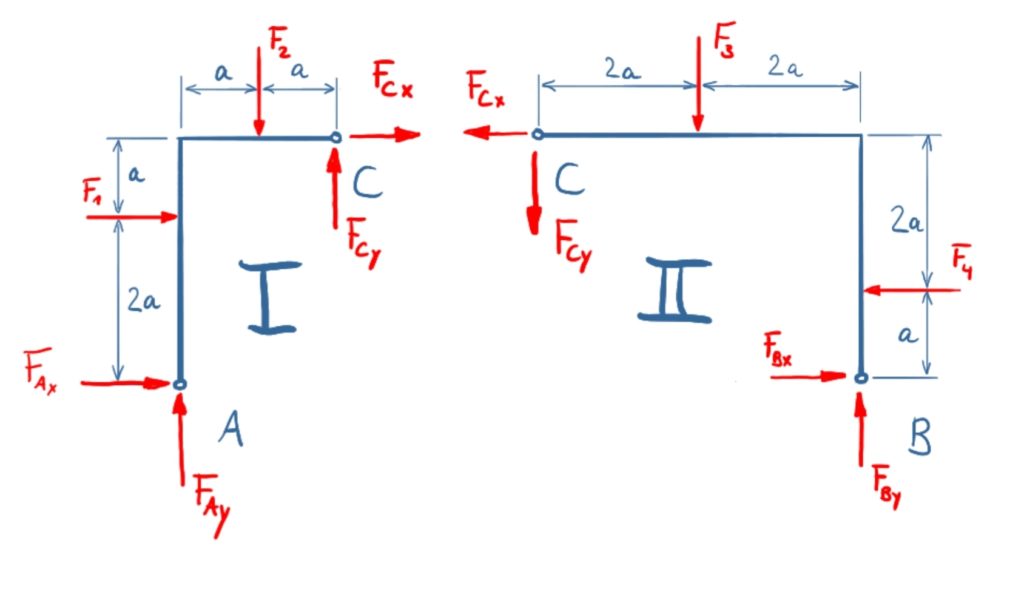
Als erster Schritt wird der Rahmen in zwei Bereiche geteilt und diese freigeschnitten. Dabei werden die Gelenkkräfte in den beiden Bereichen entgegengesetzt angetragen.
\( \DeclareMathOperator{\abs}{abs} \newcommand{\ensuremath}[1]{\mbox{$#1$}} \)
Kräftebilanzen Abschnitt I
x-Richtung
\[\tag{1} 0={F_{\mathit{Cx}}}+{F_{\mathit{Ax}}}+{F_1}\]
y-Richtung
\[\tag{2} 0={F_{\mathit{Cy}}}+{F_{\mathit{Ay}}}-{F_2}\]
Momente um A (linksdrehende Momente sind positiv)
\[\tag{3} 0=2 {F_{\mathit{Cy}}} a-3 {F_{\mathit{Cx}}} a-{F_2} a-2 {F_1} a\]
Kräftebilanzen Abschnitt II
x-Richtung
\[\tag{4} 0=-{F_{\mathit{Cx}}}+{F_{\mathit{Bx}}}-{F_4}\]
y-Richtung
\[\tag{5} 0=-{F_{\mathit{Cy}}}+{F_{\mathit{By}}}-{F_3}\]
Momente um B (linksdrehende Momente sind positiv)
\[\tag{6} 0=4 {F_{\mathit{Cy}}} a+3 {F_{\mathit{Cx}}} a+{F_4} a+2 {F_3} a\]
\[\tag{7} {F_{\mathit{Ax}}}=-{F_{\mathit{Cx}}}-{F_1}\]
Auflösen von Gleichung 3 nach FCx
\[\tag{8} {F_{\mathit{Cx}}}=\frac{2 {F_{\mathit{Cy}}}-{F_2}-2 {F_1}}{3}\]
Einsetzen von FCx in Gleichung 7
\[\tag{9} {F_{\mathit{Ax}}}=-\frac{2 {F_{\mathit{Cy}}}-{F_2}-2 {F_1}}{3}-{F_1}\]
Auflösen von Gleichung 6 nach FCy
\[\tag{10} {F_{\mathit{Cy}}}=-\frac{3 {F_{\mathit{Cx}}}+{F_4}+2 {F_3}}{4}\]
Einsetzen von FCy in Gleichung 8
\[\tag{11} {F_{\mathit{Cx}}}=\frac{-\frac{3 {F_{\mathit{Cx}}}+{F_4}+2 {F_3}}{2}-{F_2}-2 {F_1}}{3}\]
...und auflösen nach FCx
\[\tag{12} {F_{\mathit{Cx}}}=-\frac{{F_4}+2 {F_3}+2 {F_2}+4 {F_1}}{9}\]
Auflösen von Gleichung 4 nach FBx
\[\tag{13} {F_{\mathit{Bx}}}={F_{\mathit{Cx}}}+{F_4}\]
... und einsetzen von FCx liefert FBx
\[\tag{14} {F_{\mathit{Bx}}}={F_4}-\frac{{F_4}+2 {F_3}+2 {F_2}+4 {F_1}}{9}\]
Einsetzen von FCx in Gleichung 10
\[\tag{15} {F_{\mathit{Cy}}}=-\frac{-\frac{{F_4}+2 {F_3}+2 {F_2}+4 {F_1}}{3}+{F_4}+2 {F_3}}{4}\]
Auflösen von Gleichung 5 nach FBy
\[\tag{16} {F_{\mathit{By}}}={F_{\mathit{Cy}}}+{F_3}\]
... und einsetzen von FCy
\[\tag{17} {F_{\mathit{By}}}=\frac{-\frac{{F_4}+2 {F_3}+2 {F_2}+4 {F_1}}{3}+{F_2}+2 {F_1}}{2}+{F_3}\]
FCy in Gleichung 9 einsetzen
\[\tag{18} {F_{\mathit{Ax}}}=\frac{{F_4}+2 {F_3}+2 {F_2}+4 {F_1}}{9}-{F_1}\]
Auflösen der Gleichung 2 nach FAy
\[\tag{19} {F_{\mathit{Ay}}}={F_2}-{F_{\mathit{Cy}}}\]
... und einsetzen von FCy liefert die letzte fehlende Größe
\[\tag{20} {F_{\mathit{Ay}}}={F_2}-\frac{-\frac{{F_4}+2 {F_3}+2 {F_2}+4 {F_1}}{3}+{F_2}+2 {F_1}}{2}\]
Zusammenfassung der Ergebnisse
\[\tag{21} {F_{\mathit{Ax}}}=\frac{{F_4}+2 {F_3}+2 {F_2}+4 {F_1}}{9}-{F_1}\]
\[\tag{22} {F_{\mathit{Ay}}}={F_2}-\frac{-\frac{{F_4}+2 {F_3}+2 {F_2}+4 {F_1}}{3}+{F_2}+2 {F_1}}{2}\]
\[\tag{23} {F_{\mathit{Bx}}}={F_4}-\frac{{F_4}+2 {F_3}+2 {F_2}+4 {F_1}}{9}\]
\[\tag{24} {F_{\mathit{By}}}=\frac{-\frac{{F_4}+2 {F_3}+2 {F_2}+4 {F_1}}{3}+{F_2}+2 {F_1}}{2}+{F_3}\]
\[\tag{25} {F_{\mathit{Cx}}}=-\frac{{F_4}+2 {F_3}+2 {F_2}+4 {F_1}}{9}\]
\[\tag{26} {F_{\mathit{Cy}}}=\frac{-\frac{{F_4}+2 {F_3}+2 {F_2}+4 {F_1}}{3}+{F_2}+2 {F_1}}{2}\]
Einsetzen der Zahlenwerte liefert
\[\tag{27} {F_{\mathit{Ax}}}=15.56 \mathit{kN}\]
\[\tag{28} {F_{\mathit{Ay}}}=43.33 \mathit{kN}\]
\[\tag{29} {F_{\mathit{Bx}}}=-15.56 \mathit{kN}\]
\[\tag{30} {F_{\mathit{By}}}=46.67 \mathit{kN}\]
\[\tag{31} {F_{\mathit{Cx}}}=-25.56 \mathit{kN}\]
\[\tag{32} {F_{\mathit{Cy}}}=-13.33 \mathit{kN}\]
Variante 2
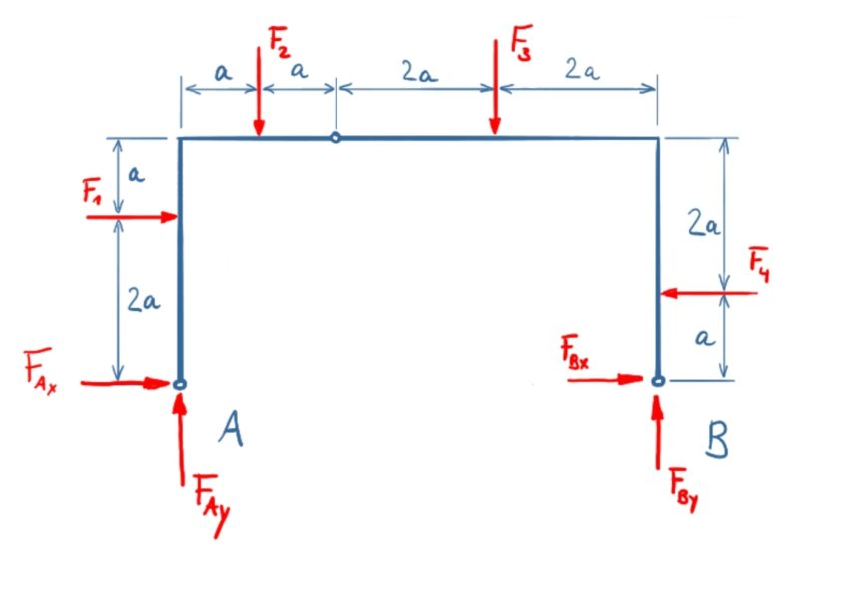
Diese Lösung wird hier ausschließlich mit den Variablen berechnet, da die Zahlenwerte vorab schon berechnet wurden.
\( \DeclareMathOperator{\abs}{abs} \newcommand{\ensuremath}[1]{\mbox{$#1$}} \)
Aufstellen der Kräfte- und Momentengleichgewichte für das Gesamtsystem
\[\tag{1} \sum F_x = 0={F_{\mathit{Bx}}}+{F_{\mathit{Ax}}}-{F_4}+{F_1}\]
\[\tag{2} \sum F_y = 0={F_{\mathit{By}}}+{F_{\mathit{Ay}}}-{F_3}-{F_2}\]
\[\tag{3} \sum M(A) = 0=6 {F_{\mathit{By}}} a+{F_4} a-4 {F_3} a-{F_2} a-2 {F_1} a\]
Die vertikale Lagerreaktion FBy kann somit unmittelbar berechnet werden:
\[\tag{4} {F_{\mathit{By}}}=-\frac{{F_4}-4 {F_3}-{F_2}-2 {F_1}}{6}\]
FBy wird nun in Gleichung 1 eingesetzt, womit FAy folgt.
\[\tag{5} 0={F_{\mathit{Ay}}}-\frac{{F_4}-4 {F_3}-{F_2}-2 {F_1}}{6}-{F_3}-{F_2}\]
\[\tag{6} {F_{\mathit{Ay}}}=\frac{{F_4}+2 {F_3}+5 {F_2}-2 {F_1}}{6}\]

Als nächstes wird die Kräftebilanz in y-Richtung für Bereich I aufgestellt, um die Gelenkkraft FCy zu berechnen:
\( \DeclareMathOperator{\abs}{abs} \newcommand{\ensuremath}[1]{\mbox{$#1$}} \)
\[\tag{7} \sum F_y = 0={F_{\mathit{Cy}}}+{F_{\mathit{Ay}}}-{F_2}\]
\[\tag{8} {F_{\mathit{Cy}}}=-\frac{{F_4}+2 {F_3}-{F_2}-2 {F_1}}{6}\]
Die Summer der Momente um A ergibt nun FCx.
\[\tag{9} \sum M(A) = 0=2 {F_{\mathit{Cy}}} a-3 {F_{\mathit{Cx}}} a-{F_2} a-2 {F_1} a\]
\[\tag{10} {F_{\mathit{Cx}}}=-\frac{{F_4}+2 {F_3}+2 {F_2}+4 {F_1}}{9}\]
Das Kräftegleichgewicht in x-Richtung für Bereich I ergibt die horizontale Lagerreaktion in A:
\[\tag{11} 0={F_{\mathit{Cx}}}+{F_{\mathit{Ax}}}+{F_1}\]
\[\tag{12} {F_{\mathit{Ax}}}=\frac{{F_4}+2 {F_3}+2 {F_2}-5 {F_1}}{9}\]
FAx wird nun in Gleichung 2 eingesetzt, womit FBx folgt.
\[\tag{13} {F_{\mathit{Bx}}}=\frac{8 {F_4}-2 {F_3}-2 {F_2}-4 {F_1}}{9}\]
Der zweite Lösungsweg führt hier schneller zu den gewünschten Ergebnissen!
Werbung




