Werbung
Diese Übung behandelt die folgenden Fragen:
- Welche Kräfte treten an reibungsfreien bzw. reibungslosen Kontaktstellen auf?
- Wie stellt man Gleichgewichtsbedingungen auf?
- Wie berechnet man Hebelarme für Kräfte an schrägen Objekten?
Aufgabe
Ein ideal glatter Stab mit der Eigengewichtskraft G soll in einen Schlitz mit der Breite B gesteckt werden, so dass sich der dargestellte Kontakt in A und B ergibt und sich der Gleichgewichtszustand einstellt. Welche Länge l muss der Stab haben, damit er sich unter dem Winkel Alpha im Gleichgewicht befindet?
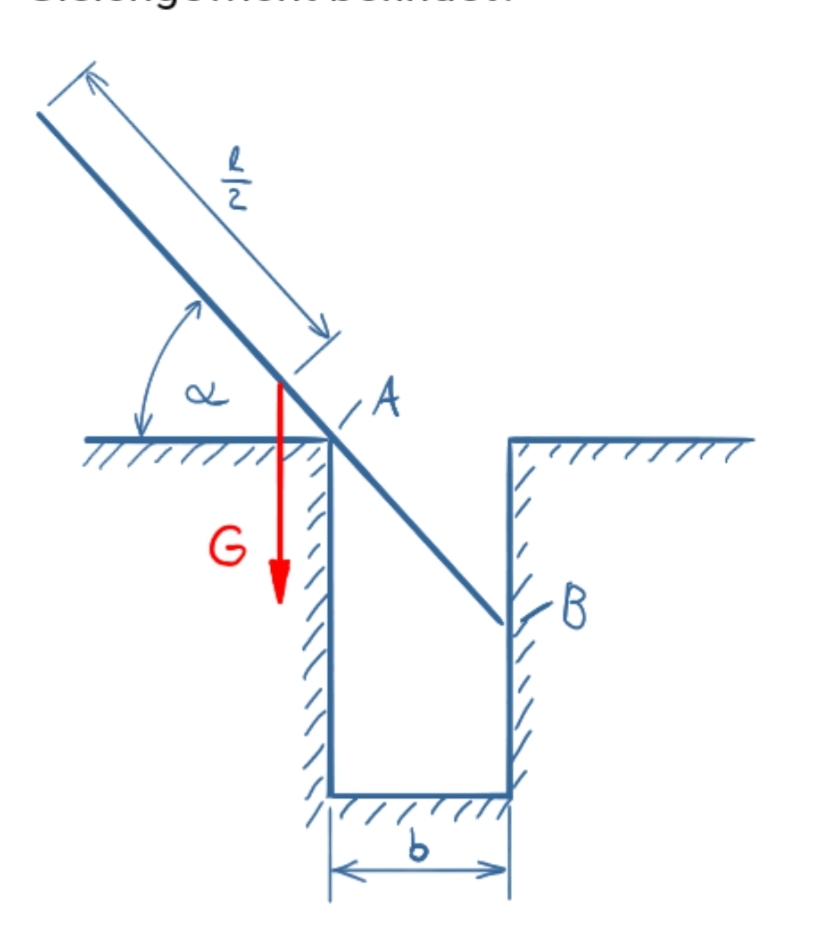
Lösung
Die im Video gezeigte Vorgehensweise zur Lösung führt zu etwas einfacheren Schritten in der Rechnung bzw. beim Umstellen der Gleichungen.
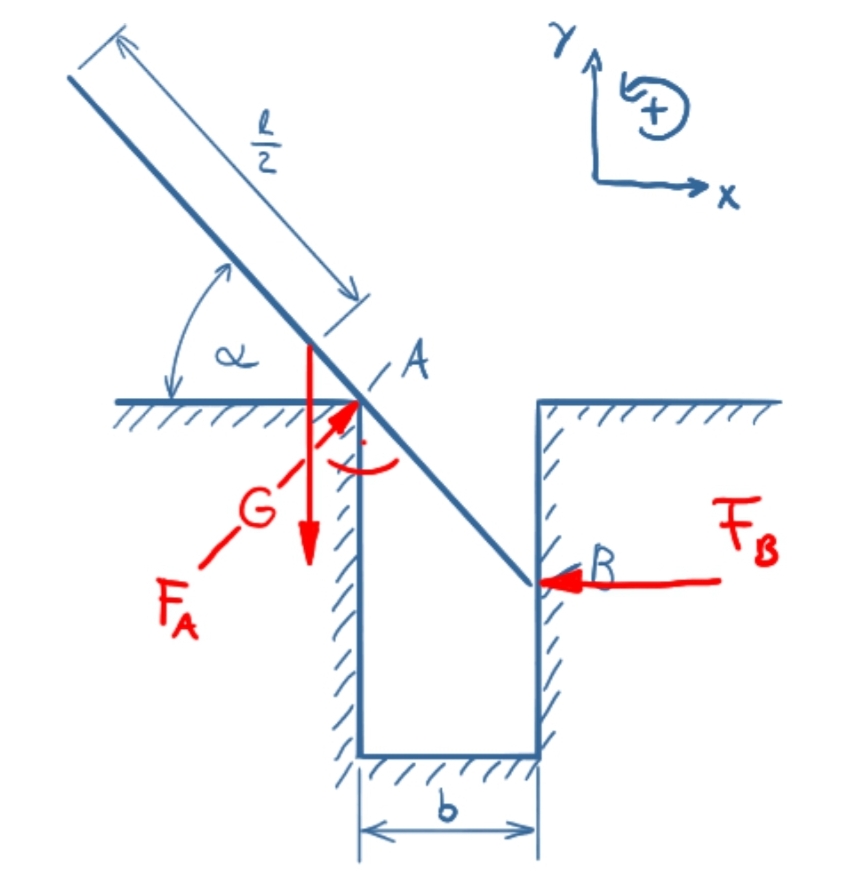
Die Eigenschaft "ideal glatt" führt zu den in der folgenden Skizze angetragenen Reaktionskräften.
\( \DeclareMathOperator{\abs}{abs} \newcommand{\ensuremath}[1]{\mbox{$#1$}} \)
Kräftebilanz in x-Richtung
\[\tag{1} 0={F_A} \sin{\left( \alpha \right) }-{F_B}\]
Kräftebilanz in y-Richtung
\[\tag{2} 0={F_A} \cos{\left( \alpha \right) }-G\]
Summe der Momente um Punkt A
\[\tag{3} 0=G\, \left( \frac{l \cos{\left( \alpha \right) }}{2}-b\right) -\frac{{F_B} b \sin{\left( \alpha \right) }}{\cos{\left( \alpha \right) }}\]
Auflösen nach l
\[\tag{4} l=\frac{2 {F_B} b \sin{\left( \alpha \right) }+2 G b \cos{\left( \alpha \right) }}{G\, {{\cos{\left( \alpha \right) }}^{2}}}\]
\[\tag{5} {F_B}={F_A} \sin{\left( \alpha \right) }\]
\[\tag{6} {F_A}=\frac{G}{\cos{\left( \alpha \right) }}\]
Einsetzen von F_A
\[\tag{7} {F_B}=\frac{G \sin{\left( \alpha \right) }}{\cos{\left( \alpha \right) }}\]
Einsetzen von F_B in die Gleichung 4
\[\tag{8} l=\frac{\frac{2 G b\, {{\sin{\left( \alpha \right) }}^{2}}}{\cos{\left( \alpha \right) }}+2 G b \cos{\left( \alpha \right) }}{G\, {{\cos{\left( \alpha \right) }}^{2}}}\]
vereinfacht:
\[\tag{9} l=\frac{2 b\, {{\sin{\left( \alpha \right) }}^{2}}+2 b\, {{\cos{\left( \alpha \right) }}^{2}}}{{{\cos{\left( \alpha \right) }}^{3}}}\]
\[\tag{10} l=\frac{2 b\, \left( {{\tan{\left( \alpha \right) }}^{2}}+1\right) }{\cos{\left( \alpha \right) }}\]
Im Hinblick auf Umformungen von Gleichungen, wie z.B. Nr. (9) oder (10) sei an dieser Stelle das Tool WolframAlpha empfohlen. In vielen Fällen kann man Terme eingeben und erhält sinnvolle Vereinfachungen oder Umformungen.
Werbung




