This exercise is about the following questions:
- Which forces occur at frictionless contact points?
- How do you establish equilibrium conditions?
- How do you calculate lever arms for forces on inclined objects?
Task
An ideally smooth rod with its own weight G should be inserted into a slot with the width B, so that the contact shown in A and B results and the state of equilibrium is established. What length l must the rod have so that it is in equilibrium at the angle Alpha?
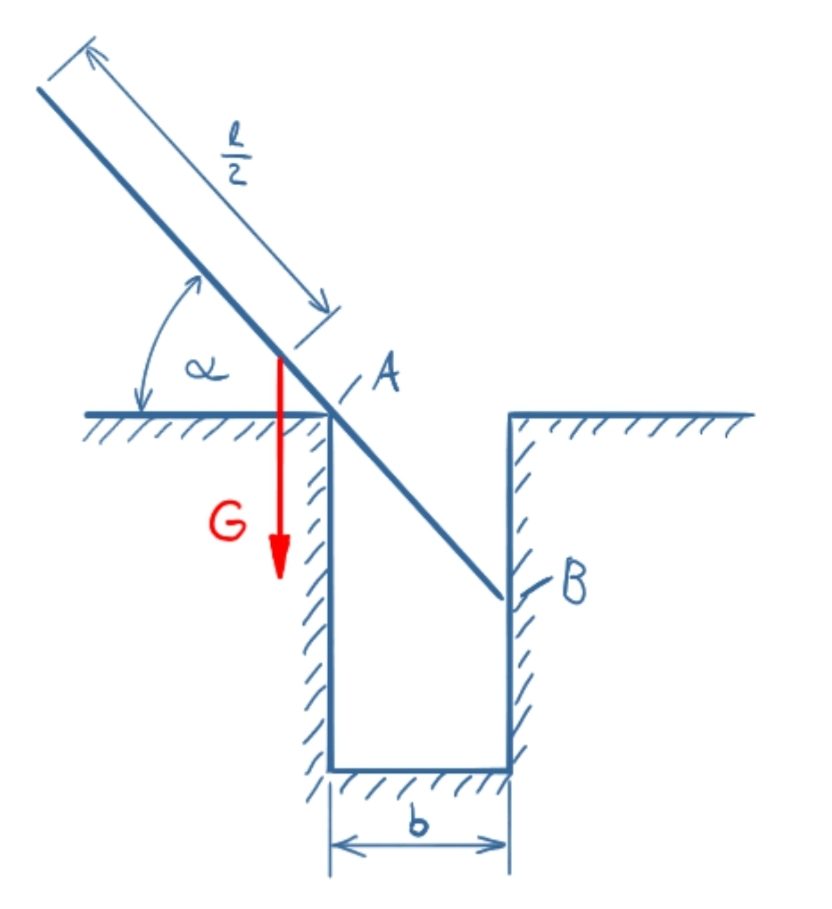
Solution
The following video is in German language, but English subtitles are available.
The way the problem is solved in the video is a little bit easier than the steps shown below.
The property "frictionless" results in the following reaction forces in the points A and B.
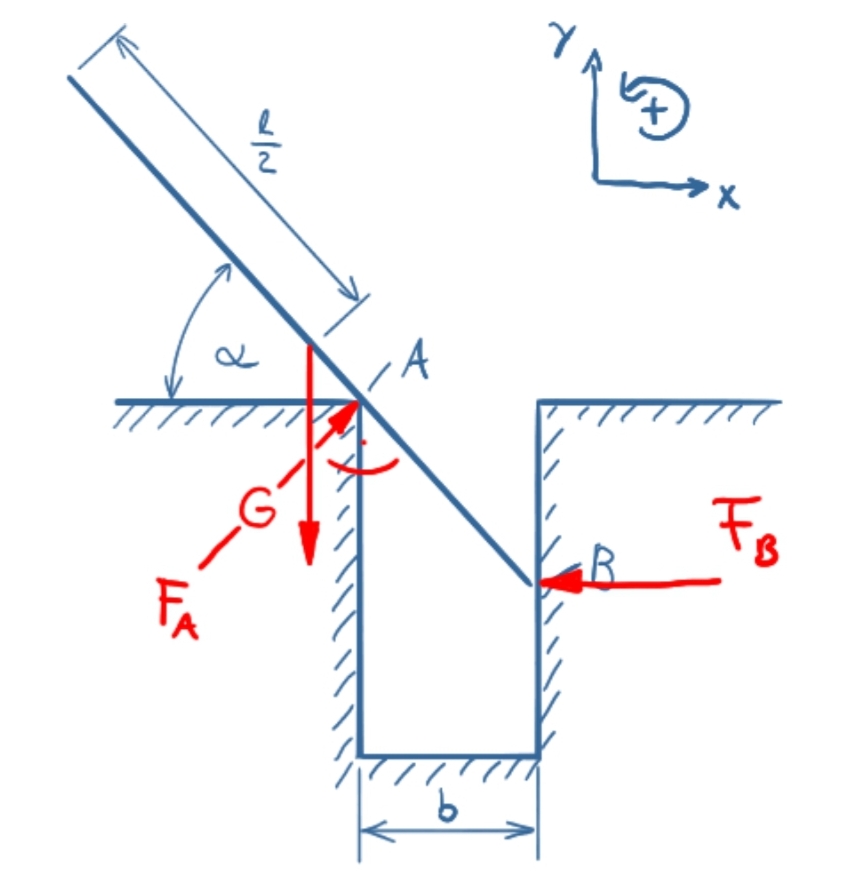
\( \DeclareMathOperator{\abs}{abs} \newcommand{\ensuremath}[1]{\mbox{$#1$}} \)
\[\tag{1} 0={F_A} \sin{\left( \alpha \right) }-{F_B}\]
\[\tag{2} 0={F_A} \cos{\left( \alpha \right) }-G\]
\[\tag{3} 0=G\, \left( \frac{l \cos{\left( \alpha \right) }}{2}-b\right) -\frac{{F_B} b \sin{\left( \alpha \right) }}{\cos{\left( \alpha \right) }}\]
\[\tag{4} l=\frac{2 {F_B} b \sin{\left( \alpha \right) }+2 G b \cos{\left( \alpha \right) }}{G\, {{\cos{\left( \alpha \right) }}^{2}}}\]
\[\tag{5} {F_B}={F_A} \sin{\left( \alpha \right) }\]
\[\tag{6} {F_A}=\frac{G}{\cos{\left( \alpha \right) }}\]
\[\tag{7} {F_B}=\frac{G \sin{\left( \alpha \right) }}{\cos{\left( \alpha \right) }}\]
\[\tag{8} l=\frac{\frac{2 G b\, {{\sin{\left( \alpha \right) }}^{2}}}{\cos{\left( \alpha \right) }}+2 G b \cos{\left( \alpha \right) }}{G\, {{\cos{\left( \alpha \right) }}^{2}}}\]
\[\tag{9} l=\frac{2 b\, {{\sin{\left( \alpha \right) }}^{2}}+2 b\, {{\cos{\left( \alpha \right) }}^{2}}}{{{\cos{\left( \alpha \right) }}^{3}}}\]
\[\tag{10} l=\frac{2 b\, \left( {{\tan{\left( \alpha \right) }}^{2}}+1\right) }{\cos{\left( \alpha \right) }}\]

