Task
A car is parked on a sloping road with the handbrake on. The handbrake acts on the rear wheels. What is the minimum coefficient of static friction required to prevent the car from slipping?
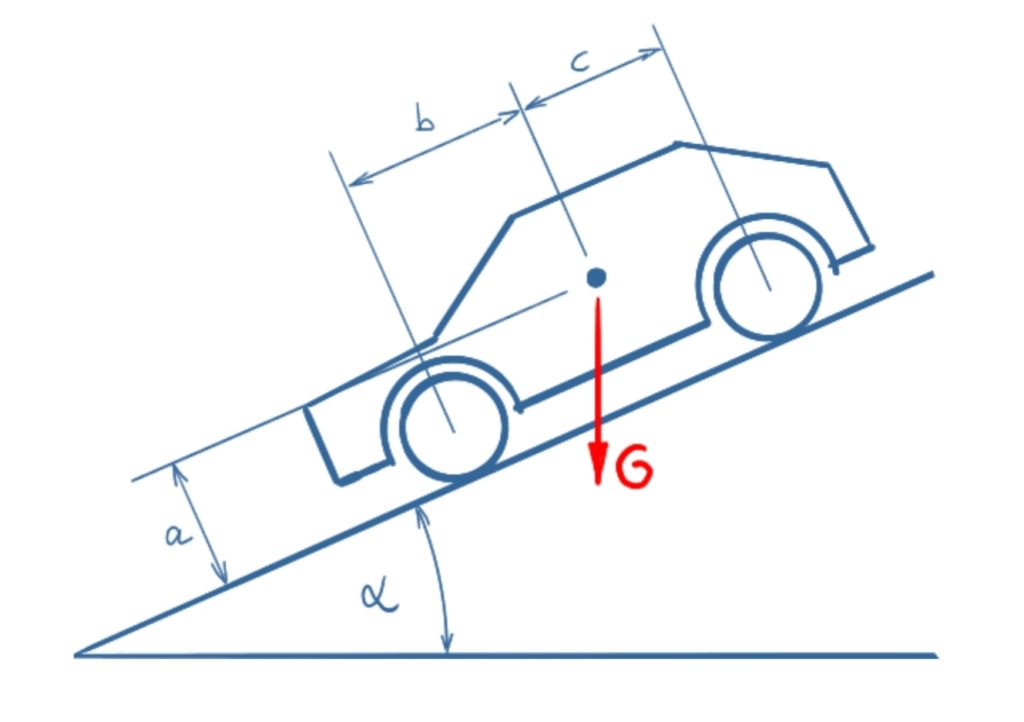
Solution
The following video is in German language, but English subtitles are available.
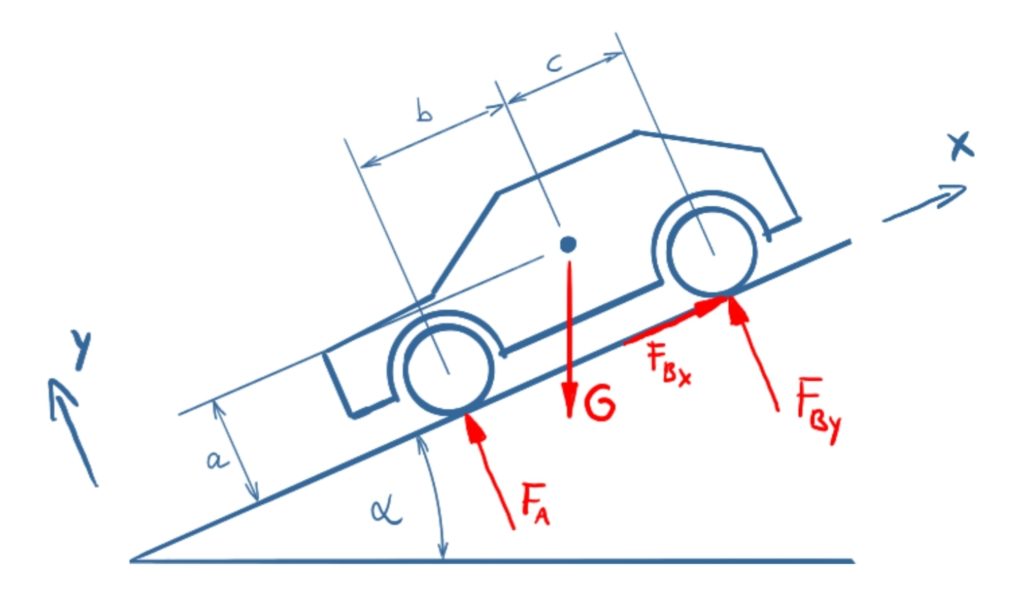
The coordinate system will be turned by the angle Alpha for the solution.
\( \DeclareMathOperator{\abs}{abs} \newcommand{\ensuremath}[1]{\mbox{$#1$}} \)
\[\tag{1} 0={F_{\mathit{Bx}}}-G \sin{\left( \alpha \right) }\]
\[\tag{2} 0=-G \cos{\left( \alpha \right) }+{F_{\mathit{By}}}+{F_A}\]
\[\tag{3} 0=G a \sin{\left( \alpha \right) }-G b \cos{\left( \alpha \right) }+{F_{\mathit{By}}} \left( c+b\right) \]
\[\tag{4} {F_{\mathit{Bx}}}={F_{\mathit{By}}} {µ_0}\]
\[\tag{5} {F_{\mathit{By}}}=\frac{{F_{\mathit{Bx}}}}{{µ_0}}\]
\[\tag{6} 0=G a \sin{\left( \alpha \right) }-G b \cos{\left( \alpha \right) }+\frac{{F_{\mathit{Bx}}} \left( c+b\right) }{{µ_0}}\]
\[\tag{7} {F_{\mathit{Bx}}}=G \sin{\left( \alpha \right) }\]
\[\tag{8} 0=\frac{G\, \left( c+b\right) \sin{\left( \alpha \right) }}{{µ_0}}+G a \sin{\left( \alpha \right) }-G b \cos{\left( \alpha \right) }\]
\[\tag{9} {µ_0}=\frac{\left( c+b\right) \sin{\left( \alpha \right) }}{b \cos{\left( \alpha \right) -}a \sin{\left( \alpha \right) }}\]
It is obvious that the weight does not play a role in the determination of the required coefficient of static friction, i.e. a discussion of the distribution of the weight force over several wheels per axle is superfluous.

