Werbung
Aufgabe
Ein Auto steht mit angezogener Handbremse auf einer abschüssigen Straße. Die Handbremse wirkt hierbei auf die Hinterräder. Wie groß muss der Haftreibungskoeffizient mindestens sein, damit das Auto nicht ins Rutschen gerät?
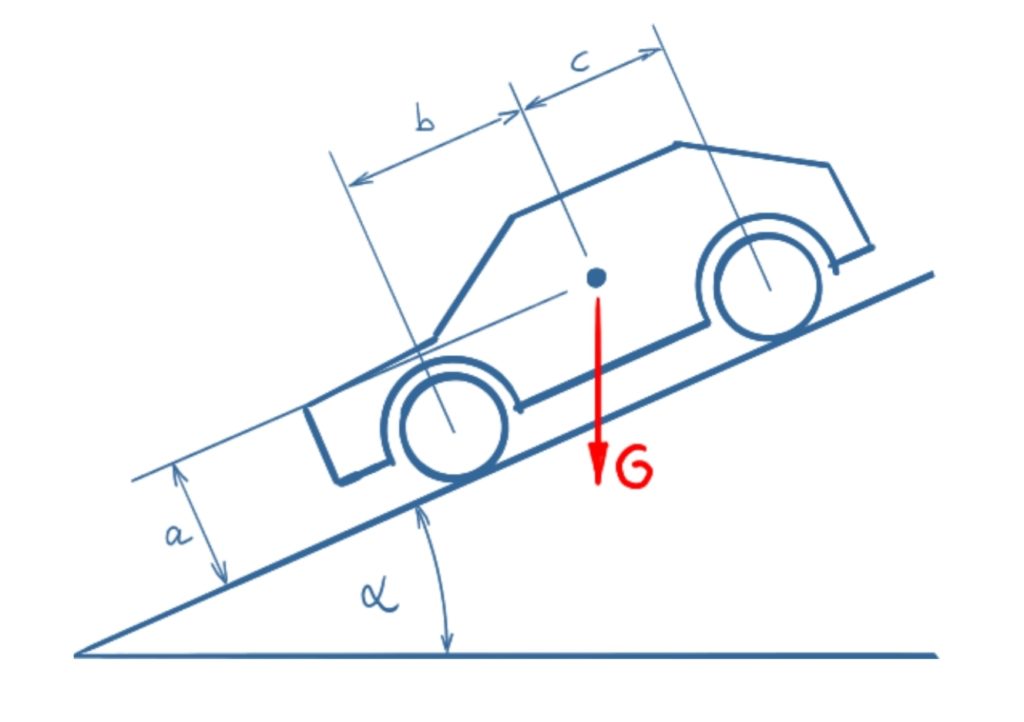
Lösung
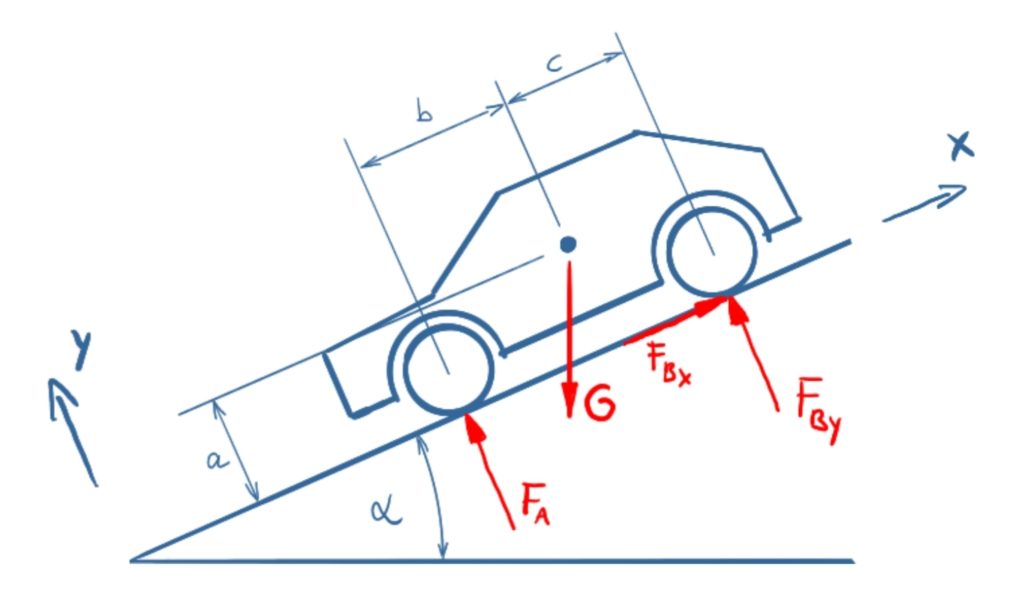
\( \DeclareMathOperator{\abs}{abs} \newcommand{\ensuremath}[1]{\mbox{$#1$}} \)
Kräftebilanz in x-Richtung
\[\tag{1} 0={F_{\mathit{Bx}}}-G \sin{\left( \alpha \right) }\]
Kräftebilanz in y-Richtung
\[\tag{2} 0=-G \cos{\left( \alpha \right) }+{F_{\mathit{By}}}+{F_A}\]
Summe der Momente um A (linksdrehende Momente positiv)
\[\tag{3} 0=G a \sin{\left( \alpha \right) }-G b \cos{\left( \alpha \right) }+{F_{\mathit{By}}} \left( c+b\right) \]
Zusammenhang zwischen Tangential- und Normalkraft am Hinterrad
\[\tag{4} {F_{\mathit{Bx}}}={F_{\mathit{By}}} {µ_0}\]
Auflösen nach F_By und in die Momentenbilanz einsetzen
\[\tag{5} {F_{\mathit{By}}}=\frac{{F_{\mathit{Bx}}}}{{µ_0}}\]
\[\tag{6} 0=G a \sin{\left( \alpha \right) }-G b \cos{\left( \alpha \right) }+\frac{{F_{\mathit{Bx}}} \left( c+b\right) }{{µ_0}}\]
Gleichung 1 auflösen nach F_Bx und in das vorige Ergebnis einsetzen
\[\tag{7} {F_{\mathit{Bx}}}=G \sin{\left( \alpha \right) }\]
\[\tag{8} 0=\frac{G\, \left( c+b\right) \sin{\left( \alpha \right) }}{{µ_0}}+G a \sin{\left( \alpha \right) }-G b \cos{\left( \alpha \right) }\]
der Mindestwert für die Haftreibung beträgt
\[\tag{9} {µ_0}=\frac{\left( c+b\right) \sin{\left( \alpha \right) }}{b \cos{\left( \alpha \right) -}a \sin{\left( \alpha \right) }}\]
Es ist offensichtlich, dass die Gewichtskraft bei der Berechnung des erforderlichen Haftreibungskoeffizienten keine Rolle spielt, d.h. eine Diskussion der Verteilung der Gewichtskraft auf mehrere Räder pro Achse ist überflüssig.
Hier gibt es weitere interessante Aufgaben zum Thema Reibung.
Werbung




