This is an exercise to introduce the capstan formula. Here you can find an online calculation tool for belt friction.
Task
A load of m = 100 kg is lowered with a rope wrapped around a pole. The wrap angle can be seen in the sketch below. The coefficient of sliding friction is µ = 0,2. What value for the holding force F is needed to lower the load without acceleration (G = m * g)?
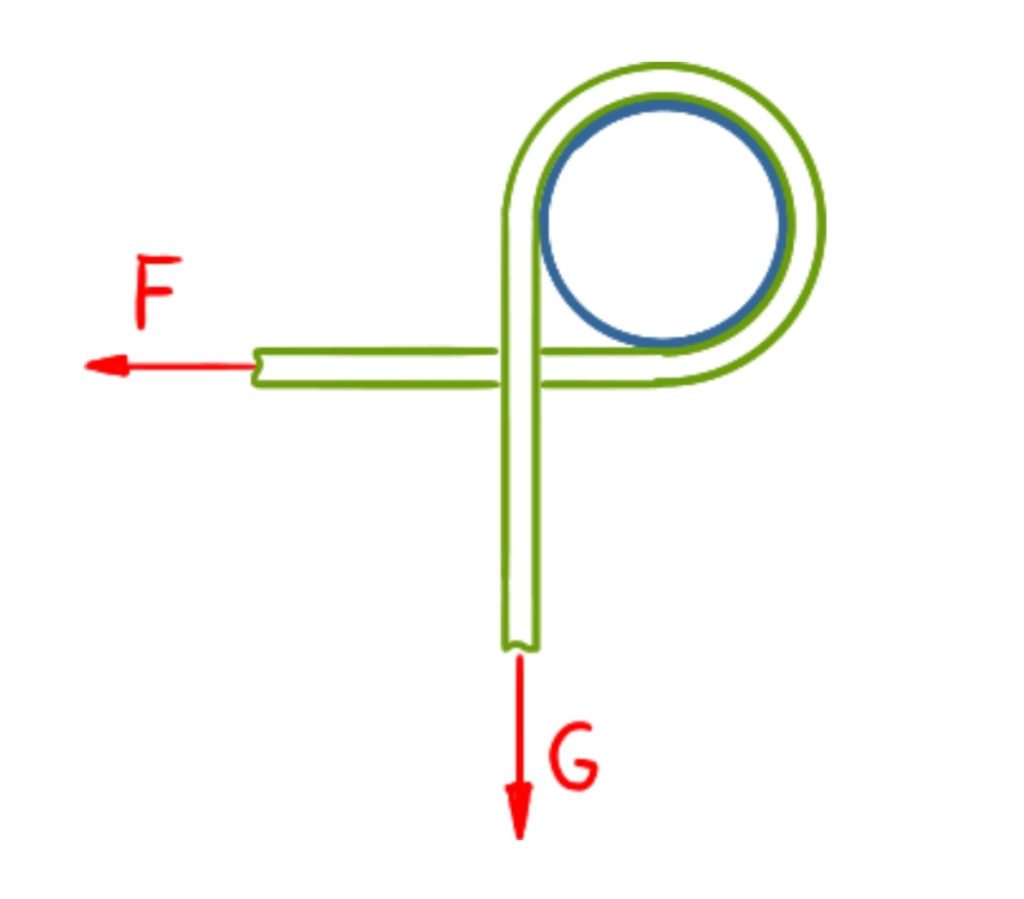
Solution
A solution video will be published soon on this channel.
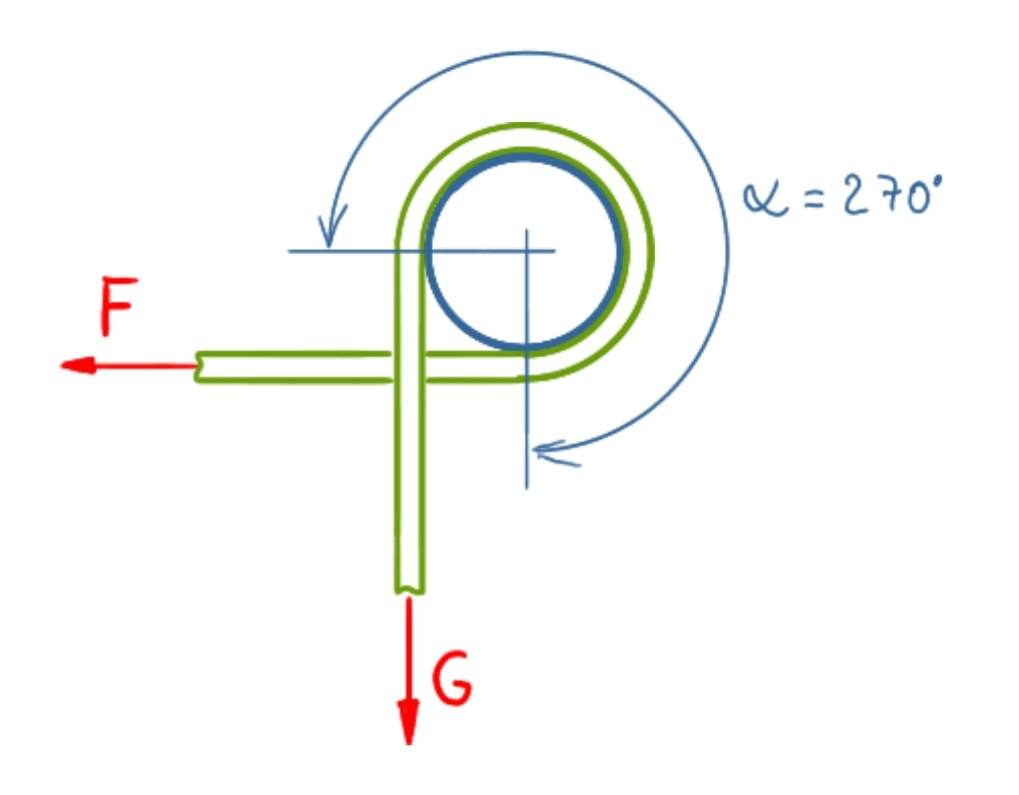
The holding force F is calculated using the Euler-Eytelwein formula (rope friction formula), which for this case is:
\[\tag{1} G = Fe^{µ\alpha}\]
With the given values and the angle of wrap alpha measured from the sketch
\[\tag{2} G =mg\]
\[\tag{3} µ = 0.2\]
\[\tag{4} \alpha = \frac{3}{2}\pi\]
this leads to
\[\tag{5} mg = Fe^{\frac{3}{10}\pi}\]
\[\tag{6} F = \frac{mg}{e^{\frac{3}{10}\pi}}\]
or in a different notation and with inserted values
\[\tag{7} F = 100 kg \cdot 9.81 \frac{m}{s^2} \cdot e^{-\frac{3}{10}\pi}\]
\[\tag{8} F = 382.26 N\]

