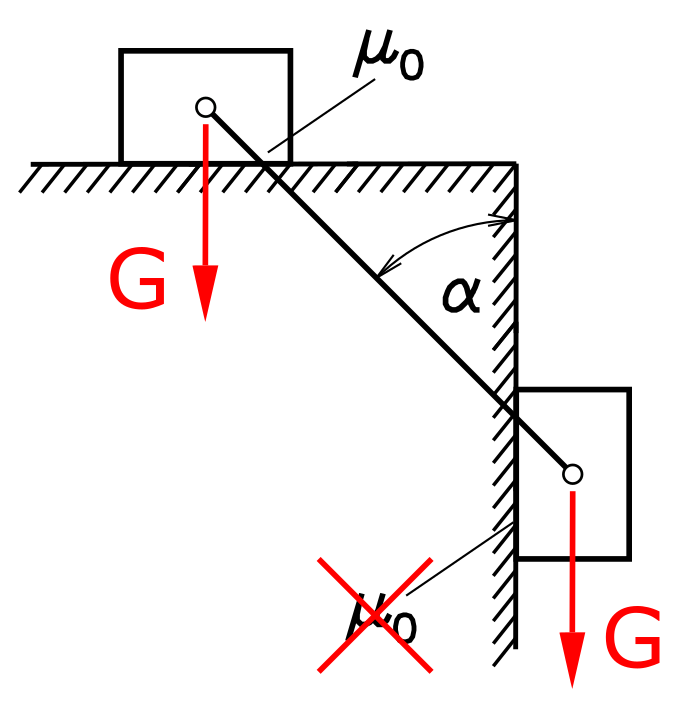
Task
Two bodies are connected with a massless rope. The coefficient of static friction for the upper body is µ0, the contact between the hanging body and the wall is frictionless. How big must the angle α be so that the two bodies are at rest?
Solution
An x-y coordinate system is defined and the two bodies are cut free. The rope is replaced by the rope force FS. The balance of forces in the x and y directions are considered separately for both bodies.
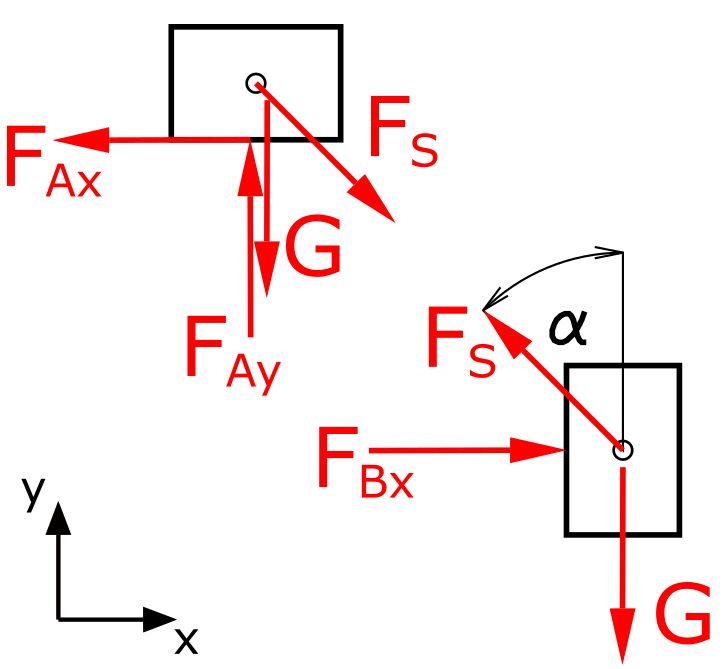
Upper body
Forces in x-direction
\[ \tag{1} \sum F_x = 0 = -F_{Ax} + F_S \cdot sin \alpha \]
Forces in y-direction
\[ \tag{2} \sum F_y = 0 = F_{Ay} - F_S \cdot cos \alpha - G \]
Hanging body
Forces in x-direction
\[ \tag{3} \sum F_x = 0 = F_{B} - F_S \cdot sin \alpha \]
Forces in y-direction
\[ \tag{4} \sum F_y = 0 = -G + F_S \cdot cos \alpha \]
The relationship between normal force and frictional force means for the forces on the upper body
\[ \tag{5} F_{Ax} = F_{Ay} \cdot µ_0 \]
The two bodies are in a state of rest as long as the x component of the rope force FS is smaller or exactly as large as the frictional force FAx.
\[ \tag{6} F_S \cdot sin \alpha \leq F_{Ax} \]
For the rope force FS can be used from equation (4), the friction force FAx follows from equation (5)
\[ \tag{7} \frac{G}{cos \alpha} \cdot sin \alpha \leq F_{Ay} \cdot µ_0 \]
FAy is determined from equation (2) and leads to
\[ \tag{8} \frac{G}{cos \alpha} \cdot sin \alpha \leq \left( \frac{G}{cos \alpha} \cdot cos \alpha + G \right) \cdot µ_0 \]
\[ \tag{9} G \cdot tan \alpha \leq 2 \cdot G \cdot µ_0 \]
\[ \tag{10} tan \alpha \leq 2 \cdot µ_0 \]
\[ \tag{11} \alpha \leq arctan \left( 2 \cdot µ_0 \right) \]
A test with two different friction values: Let's assume µ0 = 0.3
\[ \tag{12} \alpha \leq arctan (0.6) \approx 31° \]
With a smaller coefficient of friction, the angle would also have to be smaller. Assume that the coefficient of friction is µ0 = 0.2
\[ \tag{13} \alpha \leq arctan (0.4) \approx 22° \]
The result seems plausible.

