Werbung
Aufgabe
Zwei Körper sind mit einem masselosen Seil verbunden. Die Haftreibungszahl ist für den oberen Körper µ0, der Kontakt des hängenden Körpers zur Wand ist reibungslos. Wie groß muss der Winkel α sein, damit sich die beiden Körper im Ruhezustand befinden?
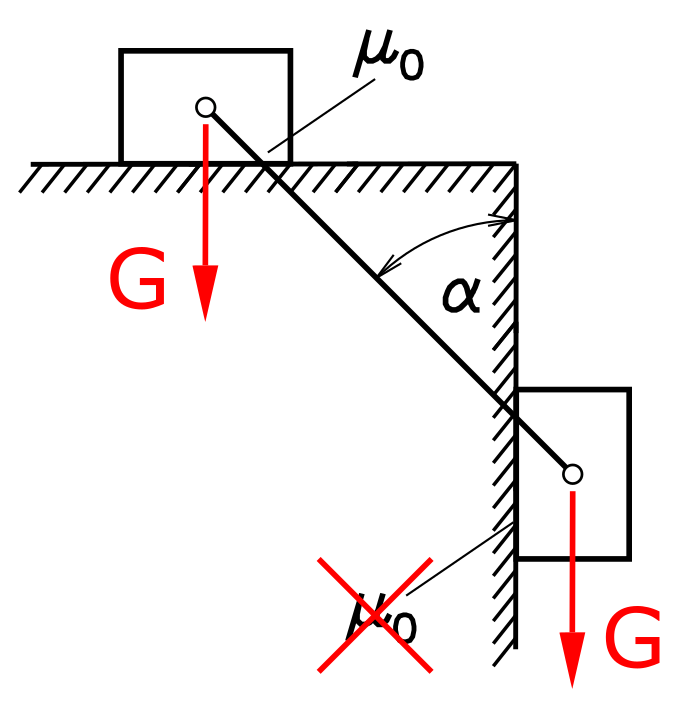
Lösung
Es wird ein x-y-Koordinatensystem festgelegt und die beiden Körper werden freigeschnitten. Das Seil wird hierbei durch die Seilkraft FS ersetzt. Die Kräftebilanzen in x- und y-Richtung werden für beide Körper separat betrachtet.
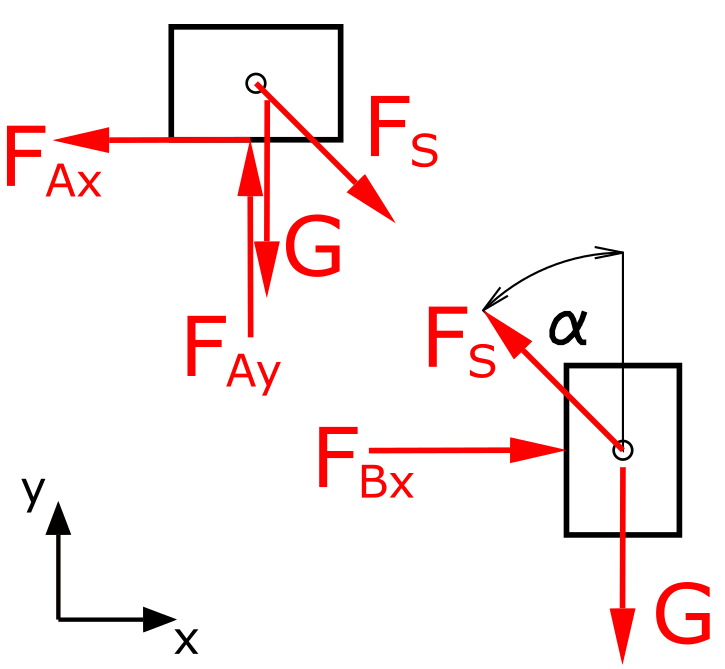
Oberer Körper
Kräftebilanz in x-Richtung
\[ \tag{1} \sum F_x = 0 = -F_{Ax} + F_S \cdot sin \alpha \]
Kräftebilanz in y-Richtung
\[ \tag{2} \sum F_y = 0 = F_{Ay} - F_S \cdot cos \alpha - G \]
Unterer Körper
Kräftebilanz in x-Richtung
\[ \tag{3} \sum F_x = 0 = F_{B} - F_S \cdot sin \alpha \]
Kräftebilanz in y-Richtung
\[ \tag{4} \sum F_y = 0 = -G + F_S \cdot cos \alpha \]
Der Zusammenhang zwischen Normalkraft und Reibkraft bedeutet für die Kräfte am oberen Körper
\[ \tag{5} F_{Ax} = F_{Ay} \cdot µ_0 \]
Die beiden Körper befinden sich im Ruhezustand, so lange die x-Komponente der Seilkraft FS kleiner oder genau so groß wie die Reibkraft FAx ist.
\[ \tag{6} F_S \cdot sin \alpha \leq F_{Ax} \]
Für die Seilkraft FS kann aus Gleichung (4) eingesetzt werden, die Reibkraft FAx folgt aus Gleichung (5)
\[ \tag{7} \frac{G}{cos \alpha} \cdot sin \alpha \leq F_{Ay} \cdot µ_0 \]
FAy wird aus Gleichung (2) bestimmt und führt zu
\[ \tag{8} \frac{G}{cos \alpha} \cdot sin \alpha \leq \left( \frac{G}{cos \alpha} \cdot cos \alpha + G \right) \cdot µ_0 \]
\[ \tag{9} G \cdot tan \alpha \leq 2 \cdot G \cdot µ_0 \]
\[ \tag{10} tan \alpha \leq 2 \cdot µ_0 \]
\[ \tag{11} \alpha \leq arctan \left( 2 \cdot µ_0 \right) \]
Eine Probe mit zwei unterschiedlichen Reibwerten. Angenommen, Reibwert 1 beträgt µ0 = 0.3
\[ \tag{12} \alpha \leq arctan (0.6) \approx 31° \]
Bei einem kleineren Reibwert müsste der Winkel ebenfalls kleiner werden. Angenommen, der Reibwert beträgt µ0 = 0.2
\[ \tag{13} \alpha \leq arctan (0.4) \approx 22° \]
Das Ergebnis scheint plausibel.
Hier gibt es weitere interessante Aufgaben und Lösungen zum Thema Reibung.
Werbung




