Werbung
In dieser Übung wird die Anwendung der Seilreibungsformel gezeigt. Einen Onlinerechner für die Seilreibung gibt es hier.
Aufgabe
Ein Last von m = 100 kg wird mit einem Seil abgelassen, das um einen Pfahl geschlungen ist. Der Gleitreibungskoeffizient beträgt µ = 0,2. Wie groß muss die Haltekraft F sein, damit die Last unbeschleunigt (G = m * g) herabgelassen wird?
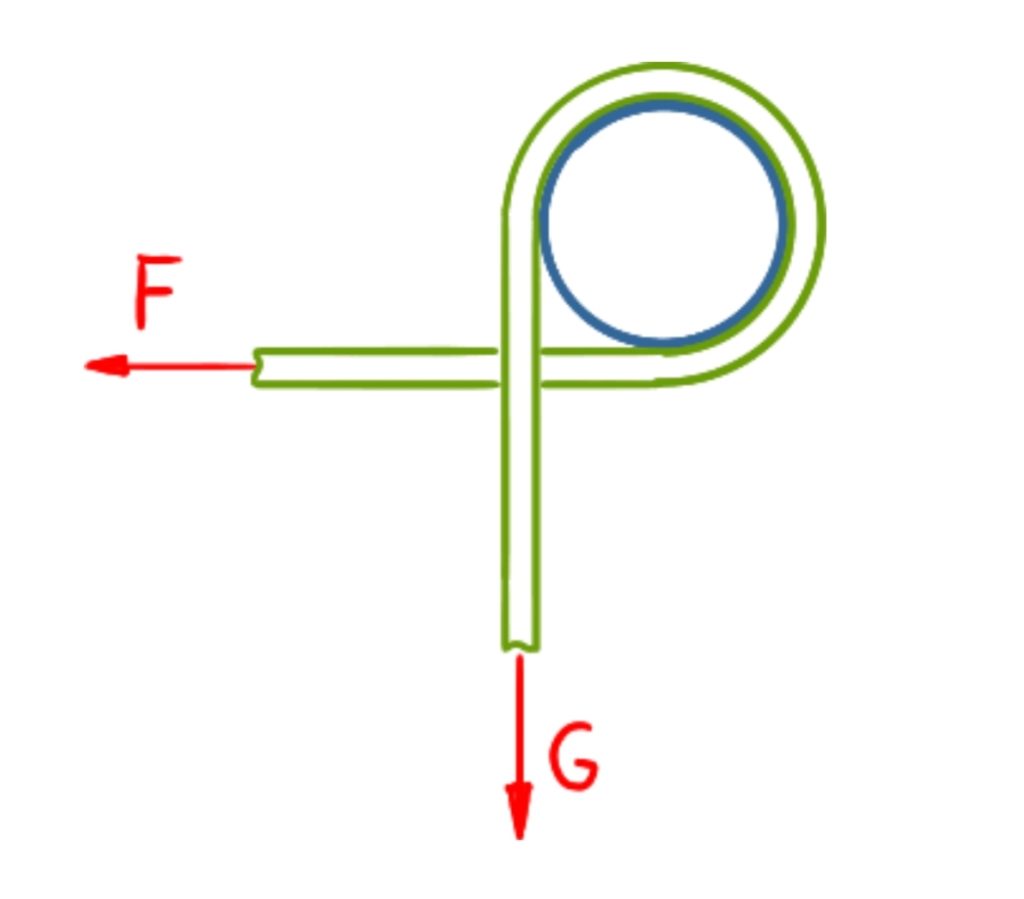
Lösung
Die Skizze zur Aufgabe enthält bereits alle erforderlichen Informationen. Zur Verdeutlichung ist nachfolgend noch der Umschlingungswinkel eingetragen.
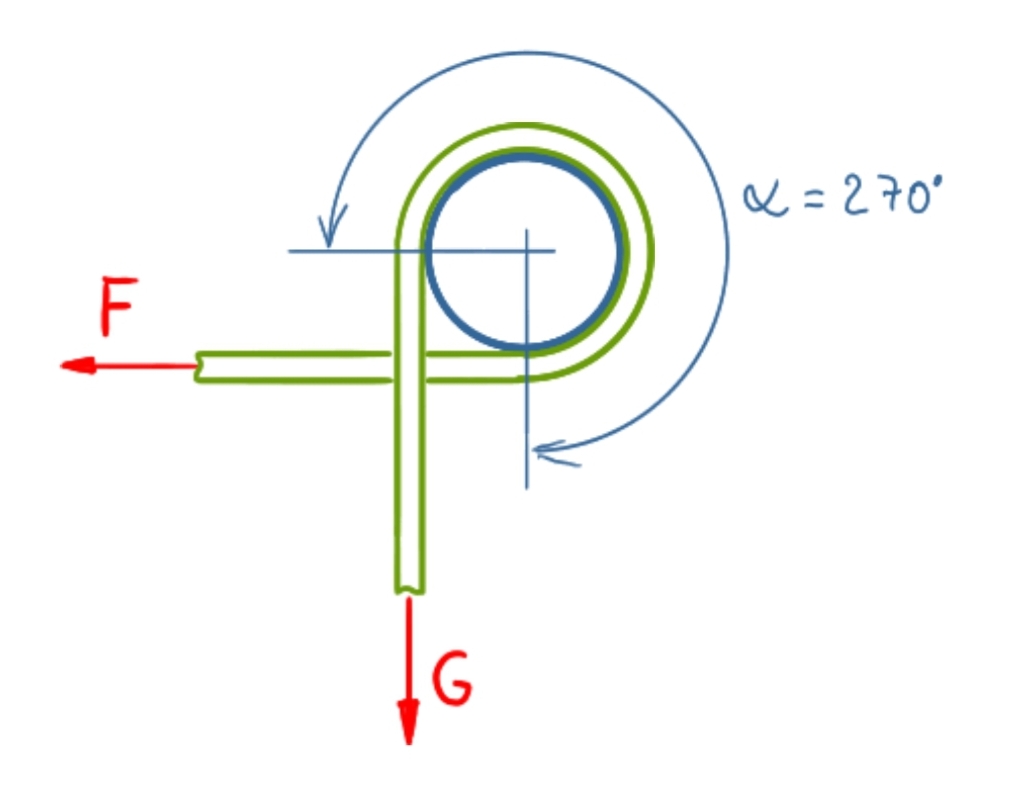
Die Haltekraft F wird mit der Euler-Eytelwein-Formel (Seilreibungsformel) berechnet, die für diesen Fall lautet:
\[\tag{1} G = Fe^{µ\alpha}\]
Mit den gegebenen Werten und dem aus der Skizze abgemessenen Umschlingungswinkel Alpha (umgerechnet in Bogenmaß)
\[\tag{2} G =mg\]
\[\tag{3} µ = 0.2\]
\[\tag{4} \alpha = \frac{3}{2}\pi\]
führt dies zu
\[\tag{5} mg = Fe^{\frac{3}{10}\pi}\]
\[\tag{6} F = \frac{mg}{e^{\frac{3}{10}\pi}}\]
bzw. in anderer Schreibweise und mit eingesetzten Werten zu
\[\tag{7} F = 100 kg \cdot 9.81 \frac{m}{s^2} \cdot e^{-\frac{3}{10}\pi}\]
\[\tag{8} F = 382.26 N\]
Hier gibt es weitere interessante Aufgaben und Lösungen zum Thema Reibung.
Werbung




