Werbung
Diese Übung behandelt folgende Fragen:
- Wie berechnet man den Flächenschwerpunkt zusammengesetzter Flächen?
- Wie addiert man Einzelschwerpunkte?
Aufgabe
Für den Querschnitt von zwei aneinander gesetzten Profilen soll der gemeinsame Flächenschwerpunkt bestimmt werden.
Gegeben: a = 50 mm, b = 22 mm, c = 70 mm, d = 20 mm.
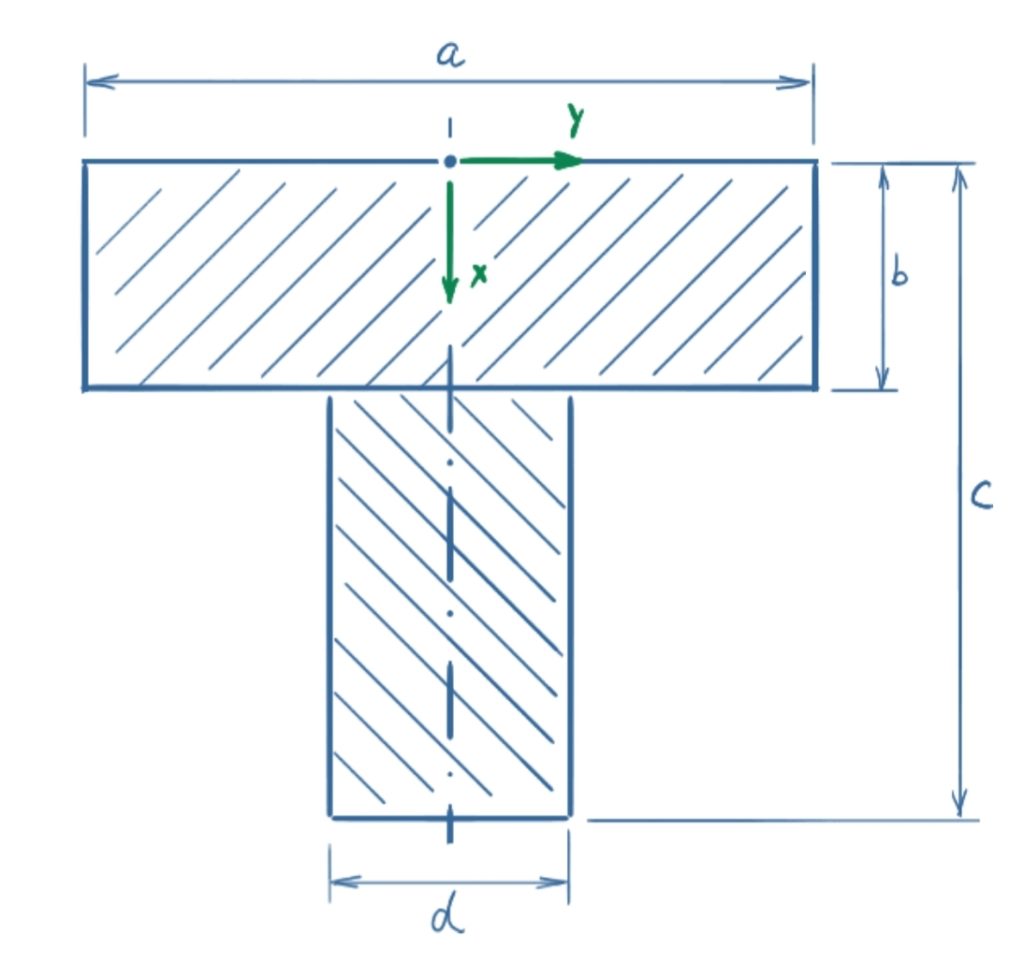
Lösung
Da es sich bei den aneinandergesetzten Profilen um reine Rechteckquerschnitte handelt, lassen sich die einzelnen Flächenschwerpunkte einfach bestimmen.
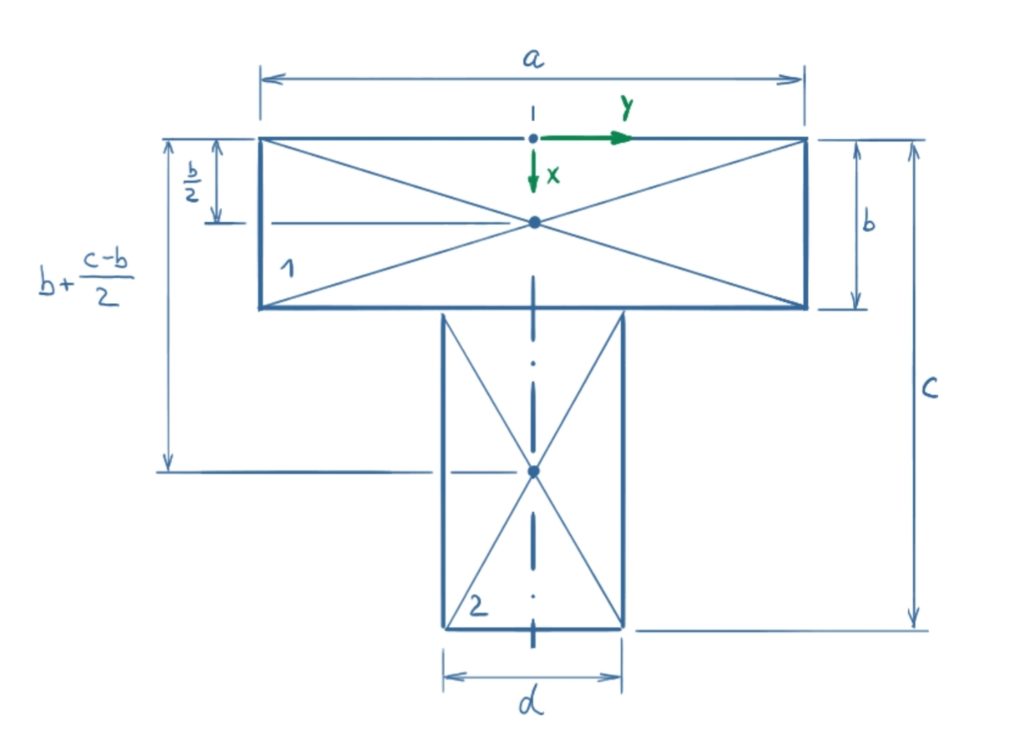
Beide Flächen sind spiegelsymmetrisch um die x-Achse, also genügt die Betrachtung der x-Koordinate. Die allgemeine Gleichung für die x-Koordinate des Flächenschwerpunkts lautet:
\[ \tag{1} x_S = \frac{\sum A_i \cdot x_i}{\sum A_i} \]
Bei mehreren Flächen bietet es sich an, die einzelnen Flächeninhalte und Einzelschwerpunkte in einer Tabelle aufzuführen:
| \[ i \] | \[ A_i \] | \[ x_i \, in \, mm \] | \[ A_i \cdot x_i\, in \,mm^3 \] |
|---|---|---|---|
| 1 | 1.100 | 11 | 12.100 |
| 2 | 960 | 46 | 44.160 |
| \[ \sum \] | 2.060 | 56.260 |
\[ \tag{2} x_S = \frac{56260mm^3}{2060mm^2} \]
\[ \tag{3} x_S = 27,3 mm \]
Und der Vollständigkeit halber:
\[ \tag{4} y_S = 0 mm \]
Damit ist die Vorgehensweise für den Flächenschwerpunkt zusammengesetzter Flächen gezeigt. Wie man vorgeht, wenn eine der Flächen eine Bohrung oder ein Loch hat, wird in dieser Übung gezeigt.
Werbung




