This exercise is about the following questions:
- How to calculate the common centroid of composited areas?
- How to determine the centroid of a rectangle?
Task
For the cross-section of two adjacent profiles, the common center of area is to be determined.
Given: a = 50 mm, b = 22 mm, c = 70 mm, d = 20 mm.
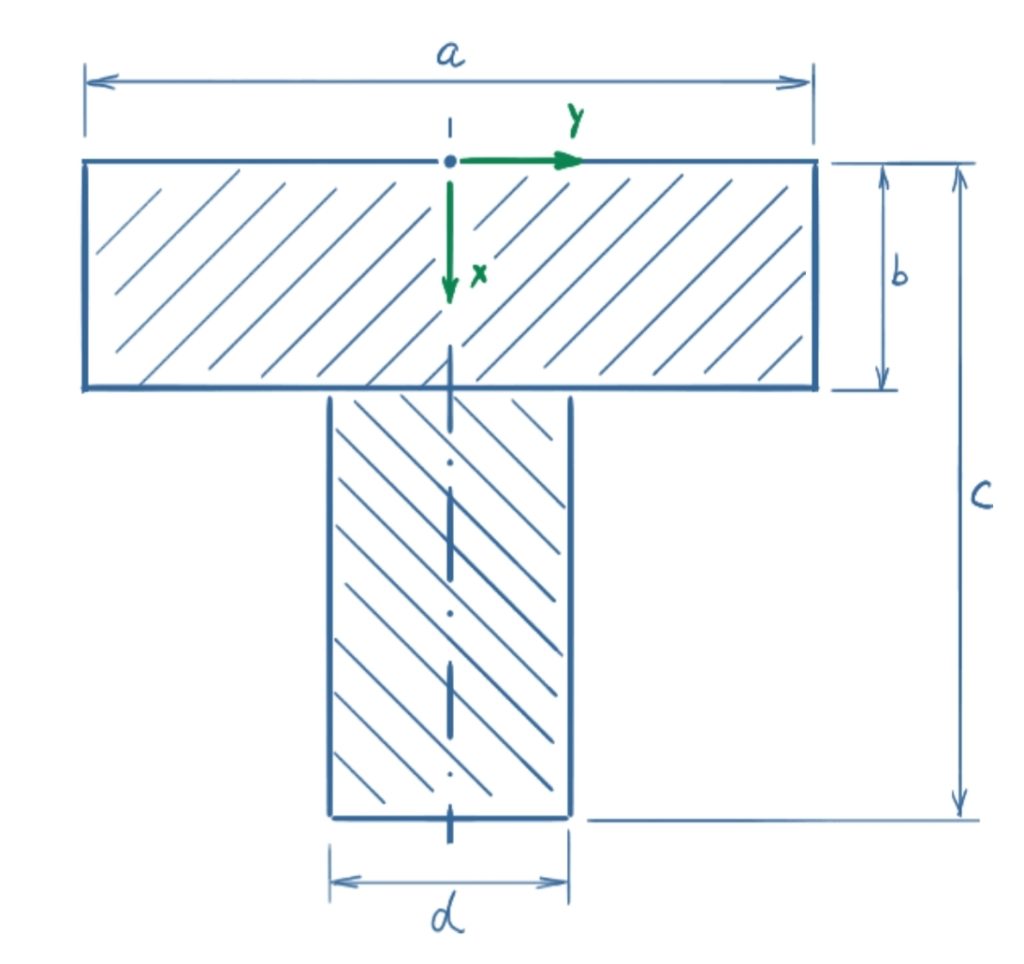
Solution
Since the adjacent profiles are purely rectangular cross-sections, the individual centroids can be easily determined.
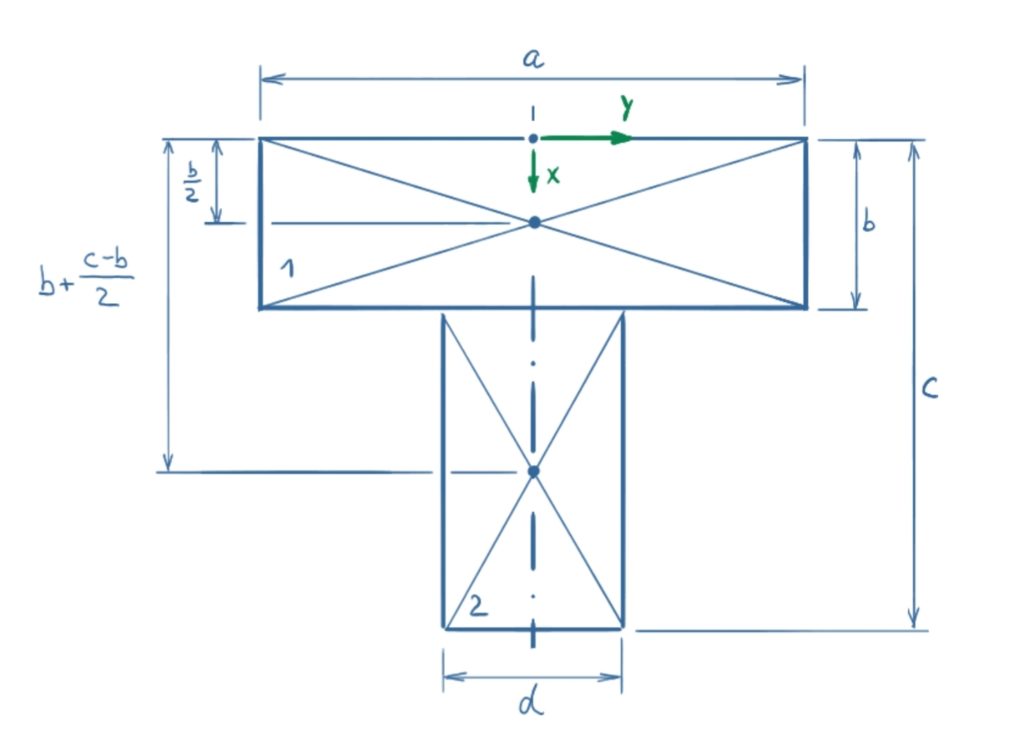
Both surfaces are mirror-symmetrical about the x-axis, so it is sufficient to consider the x-coordinate. The general equation for the x-coordinate of the centre of area is:
\[ \tag{1} x_S = \frac{\sum A_i \cdot x_i}{\sum A_i} \]
If there are several areas, it is advisable to list the individual areas and the relevant coordinates of the individual centre points in a table:
| \[ i \] | \[ A_i \] | \[ x_i \, in \, mm \] | \[ A_i \cdot x_i\, in \,mm^3 \] |
|---|---|---|---|
| 1 | 1.100 | 11 | 12.100 |
| 2 | 960 | 46 | 44.160 |
| \[ \sum \] | 2.060 | 56.260 |
\[ \tag{2} x_S = \frac{56260mm^3}{2060mm^2} \]
\[ \tag{3} x_S = 27,3 mm \]
And for the sake of completeness:
\[ \tag{4} y_S = 0 mm \]

