This exercise is about the usage of the belt friction formula. Common friction values can be found here. A tool for the calculation of belt friction is here.
Task
A brake with a double-acting operating lever is operated with the force F. The maximum braking torques in clockwise and counter-clockwise rotation must be determined.
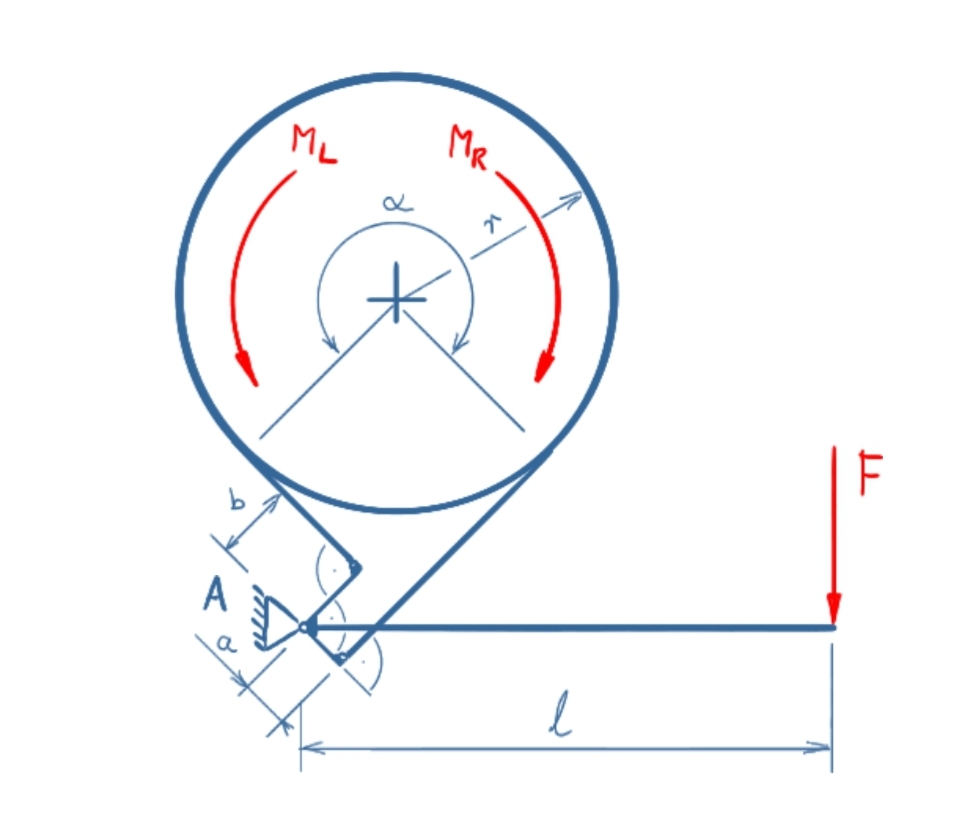
Solution
The band brake is divided into two sections: the operating lever and the drum with the band. The equilibrium of moments on the drum are considered separately for right-hand and left-hand rotation.
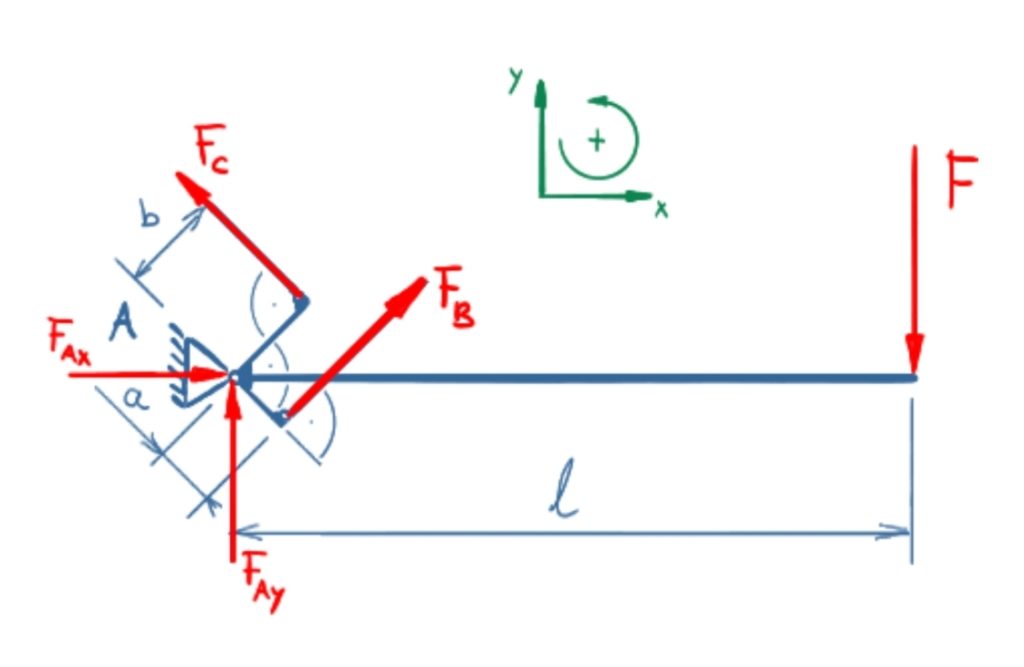
Moments at the operating lever
\[ \tag{1} \sum M(A) = 0 = F_C \cdot b + F_B \cdot a - F \cdot l \]
Left-hand rotation
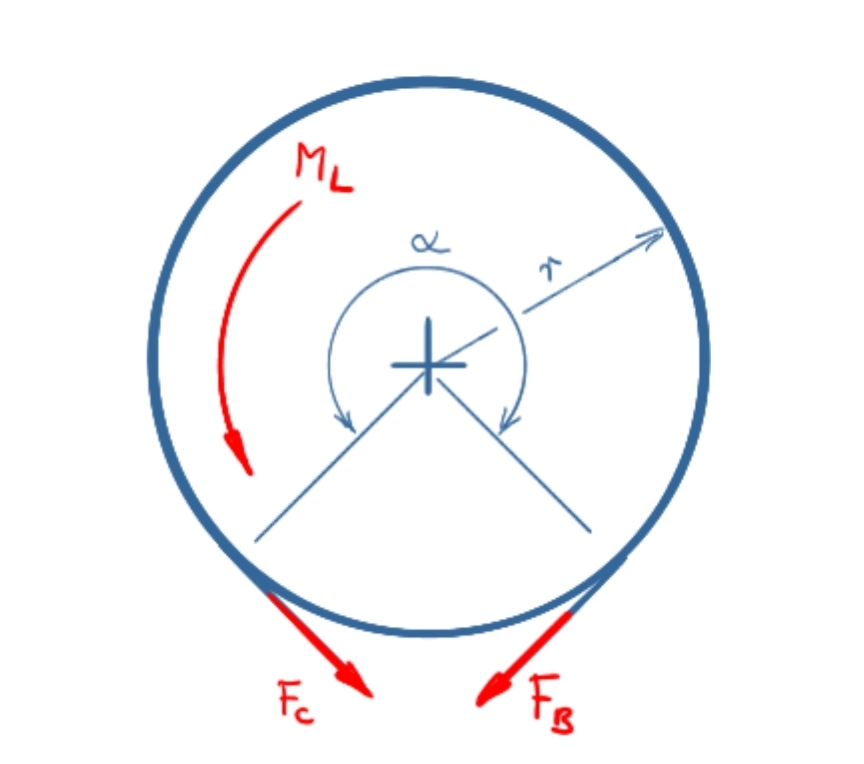
Moments at the brake drum
\[ \tag{2} \sum M = 0 = F_C \cdot r - F_B \cdot r + M_L \]
The rope friction formula (Euler-Eytelwein) provides the relationship between the forces in the working belt and the loose belt:
\[ \tag{3} F_B \leq F_C \cdot e^{µ \cdot \alpha} \]
FB used in equation (1) delivers
\[ \tag{4} 0 = F_C \cdot b + F_C \cdot e^{µ \cdot \alpha} \cdot a - F \cdot l \]
\[ \tag{5} F_C \cdot b + F_C \cdot e^{µ \cdot \alpha} \cdot a = F \cdot l \]
\[ \tag{6} F_C = \frac{F \cdot l}{b + e^{µ \cdot \alpha} \cdot a} \]
FB and FC can now be used in equation (2)
\[ \tag{7} 0 = \frac{F \cdot l}{b + e^{µ \cdot \alpha} \cdot a} \cdot r - \frac{F \cdot l}{b + e^{µ \cdot \alpha} \cdot a} \cdot e^{µ \cdot \alpha} \cdot r + M_L \]
\[ \tag{8} M_L = \frac{F \cdot l}{b + e^{µ \cdot \alpha} \cdot a} \cdot e^{µ \cdot \alpha} \cdot r - \frac{F \cdot l}{b + e^{µ \cdot \alpha} \cdot a} \cdot r \]
\[ \tag{9} M_L = \frac{F \cdot l \cdot r}{b + e^{µ \cdot \alpha} \cdot a} \cdot \left(e^{µ \cdot \alpha} - 1 \right) \]
So the maximum breaking torque for the left-hand rotation of the band brake is determined.
Right-hand rotation
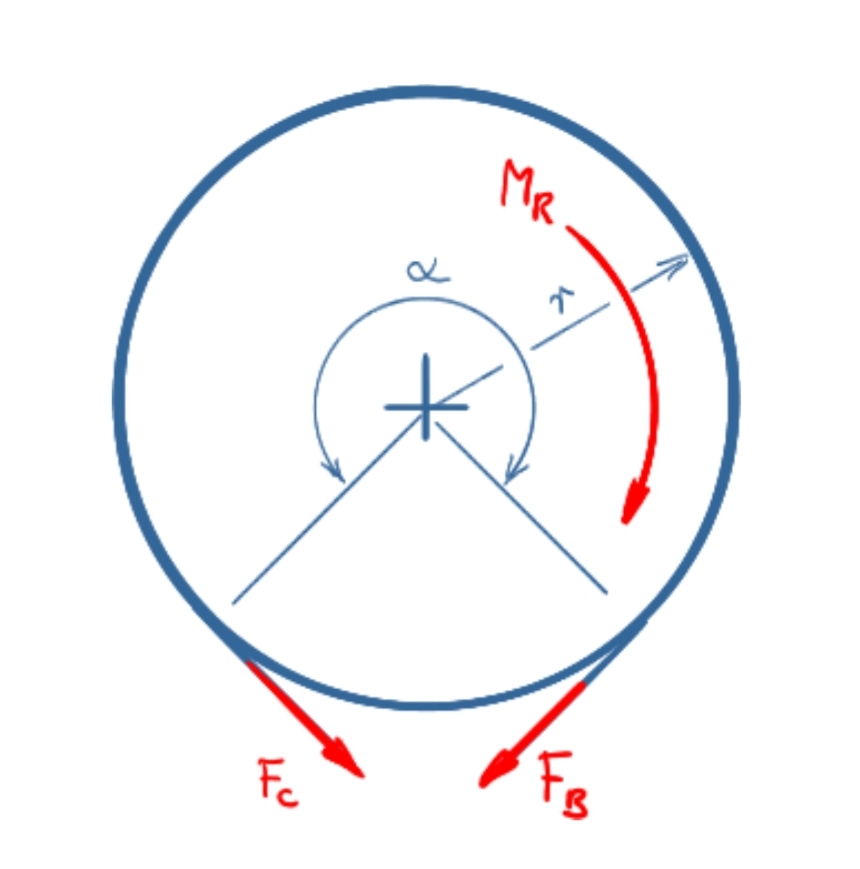
Moments at the brake drum
\[ \tag{10} \sum M = 0 = F_C \cdot r - F_B \cdot r - M_R \]
The rope friction formula is in this case:
\[ \tag{11} F_C \leq F_B \cdot e^{µ \cdot \alpha} \]
\[ \tag{12} F_B = F_C \cdot e^{-µ \cdot \alpha} \]
FB used in equation (1) delivers
\[ \tag{13} 0 = F_C \cdot b + F_C \cdot e^{-µ \cdot \alpha} \cdot a - F \cdot l \]
\[ \tag{14} F_C = \frac{F \cdot l}{b + e^{-µ \cdot \alpha} \cdot a} \]
FB and FC can now be used in equation (10)
\[ \tag{15} 0 = \frac{F \cdot l}{b + e^{-µ \cdot \alpha} \cdot a} \cdot r - \frac{F \cdot l}{b + e^{-µ \cdot \alpha} \cdot a} \cdot e^{-µ \cdot \alpha} \cdot r - M_R \]
\[ \tag{16} M_R = \frac{F \cdot l}{b + e^{-µ \cdot \alpha} \cdot a} \cdot r - \frac{F \cdot l}{b + e^{-µ \cdot \alpha} \cdot a} \cdot e^{-µ \cdot \alpha} \cdot r \]
\[ \tag{17} M_R = \frac{F \cdot l \cdot r}{b + e^{-µ \cdot \alpha}} \cdot \left( 1 - e^{-µ \cdot \alpha} \right) \]
So the maximum breaking torque for the right-hand rotation of the band brake is determined.
Here is a collection of further interesting exercises and solutions regarding friction.

