Werbung
Dies ist eine Übungsaufgabe zum einachsigen Spannungszustand, es werden folgende Fragen behandelt:
- Wie berechnet man die Spannung in einem Stab, der von seinem Eigengewicht belastet wird?
- Wie zeichnet man einen Mohrschen Spannungskreis für einen einachsigen Spannungszustand?
Aufgabe
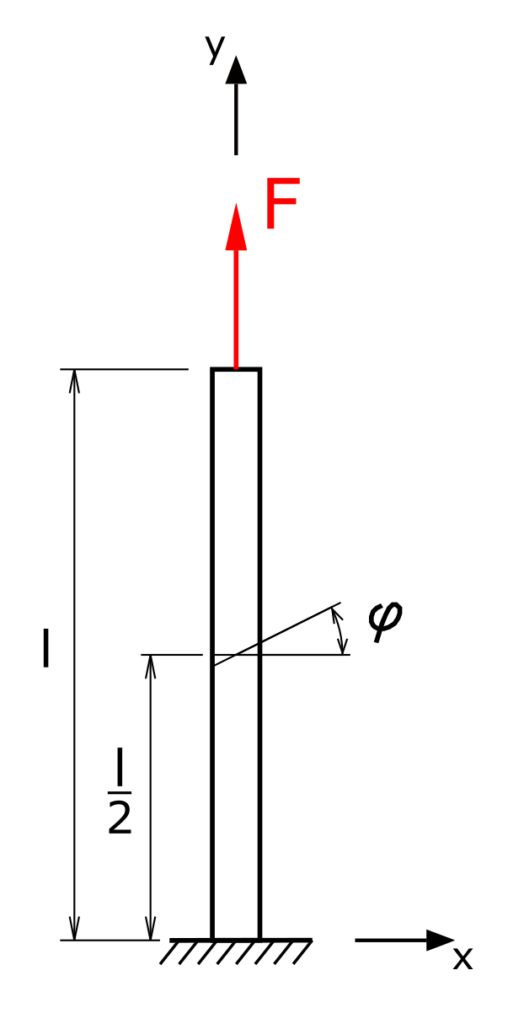
Ein dünner Stab mit der Querschnittsfläche q wird durch die Kraft F und sein Eigengewicht belastet. Für die Stelle y = l/2 soll der MOHRsche Spannungskreis gezeichnet werden. Aus dem Spannungskreis sind die Spannungen σφ und τφ zu bestimmen!
Die folgenden Parameter sind gegeben:
- F = 1 N
- l = 0,4 m
- ρ = 10000 kg/m³
- q = 1 cm²
- φ = 30°
- g = 9,81 m/s²
Lösung
Im ersten Schritt müssen die inneren Kräfte an der Stelle y = l/2 bestimmt werden. Da es keinerlei Querkräfte oder Momente gibt, herrscht im Stab ein einachsiger Spannungszustand.
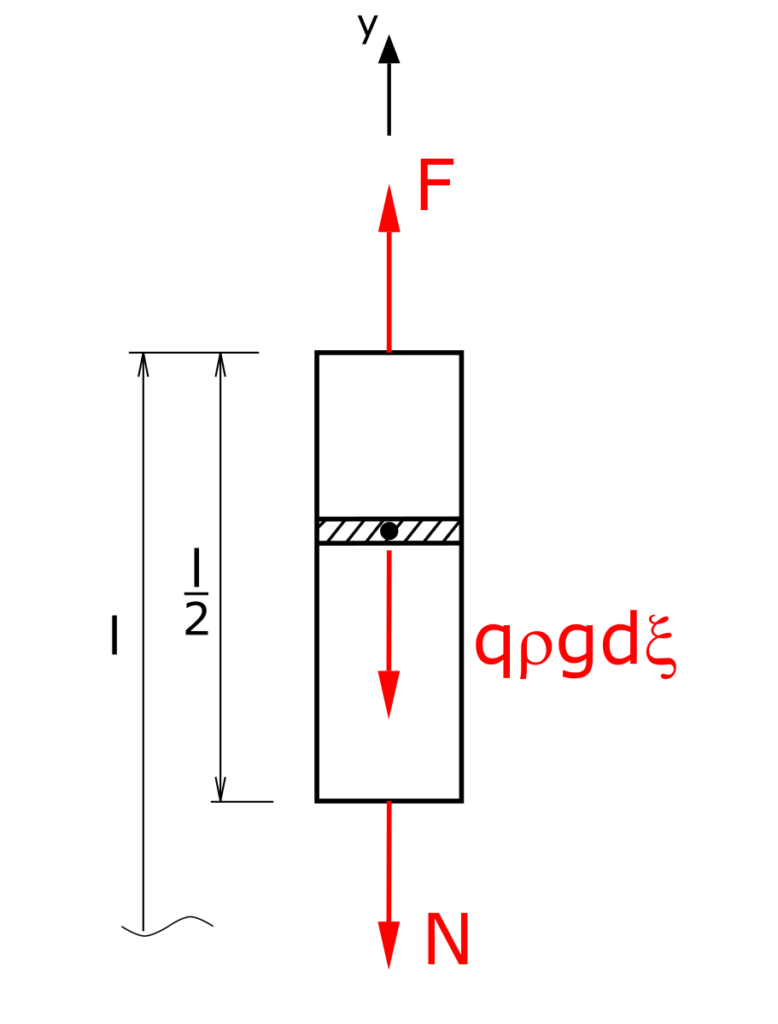
Zusätzlich zur Normalkraft an der Stelle y=l/2 wirkt die Gewichtskraft G, hier durch Integration des Terms qρg entlang der in y-Richtung laufenden Koordinate ξ zu berechnen ist. Dabei müssen natürlich die unterschiedlichen Dimensionen berücksichtigt werden. Die Spannung an der betrachteten Stelle y=l/2 wird im Folgenden als σ0 bezeichnet.
Das Kräftegleichgewicht setzt sich damit zusammen aus
\[ \tag{1} \sum F_y = 0 = -\int_{l/2}^l{q\cdot \rho \cdot g \,d\xi} - N + F \]
Da für den betrachteten Querschnitt die Spannung gesucht ist, kann diese Gleichung durch Division mit der Querschnittsfläche in die Spannungsform gebracht werden.
\[ \tag{2} 0 = -\int_{l/2}^l{\rho \cdot g \,d\xi} - \frac{N}{q} + \frac{F}{q} \]
Die Spannung σ0 ist
\[ \tag{3} \sigma_0 = \frac{N}{q} \]
und damit wird aus Gleichung (2)
\[ \tag{4} 0 = -\int_{l/2}^l{\rho \cdot g \,d\xi} - \sigma_0 + \frac{F}{q} \]
so dass nun die gesuchte Spannung berechnet werden kann.
\[ \tag{5} \sigma_0 = \frac{F}{q}-\rho \cdot g \cdot \frac{l}{2} \]
Für die weitere Betrachtung ist es sinnvoll, Pascal als Einheit für die Spannung zu verwenden. Unter Anwendung großzügiger Rundung ergibt sich die Normalspannung zu
\[ \tag{6} \sigma_0 = - 10000Pa \]
Der Mohrsche Spannungskreis
Die berechnete Normalspannung bildet den Durchmesser des Mohr'schen Spannungskreises. Dieser ist, da die Spannung negativ ist, auf der linken Seite der Vertikalachse abzutragen. Der fertige Kreis sieht folgendermaßen aus:
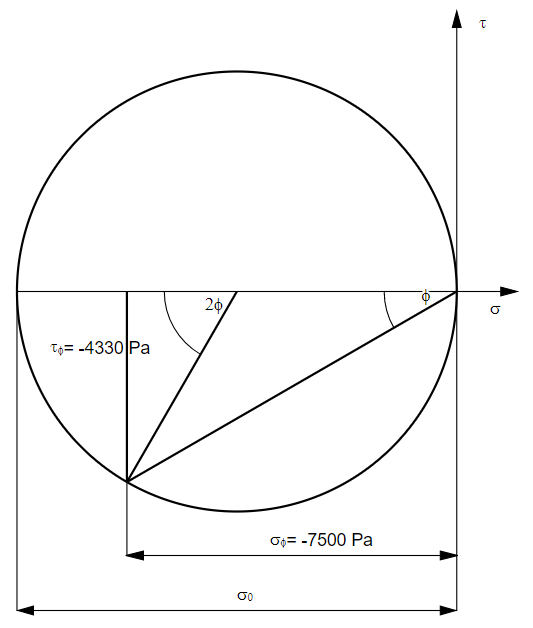
Die gesuchten Spannungen sind in der o.a. Abbildung bereits enthalten.
Die o.a. Abbildung in dieser Übungsaufgabe zum einachsigen Spannungszustand wurde mit dem Onlinegenerator für Mohrsche Spannungskreise (einachsig) erstellt, mit dem man schnell verschiedene Varianten durchspielen kann.
Werbung




