Werbung
Aufgabe
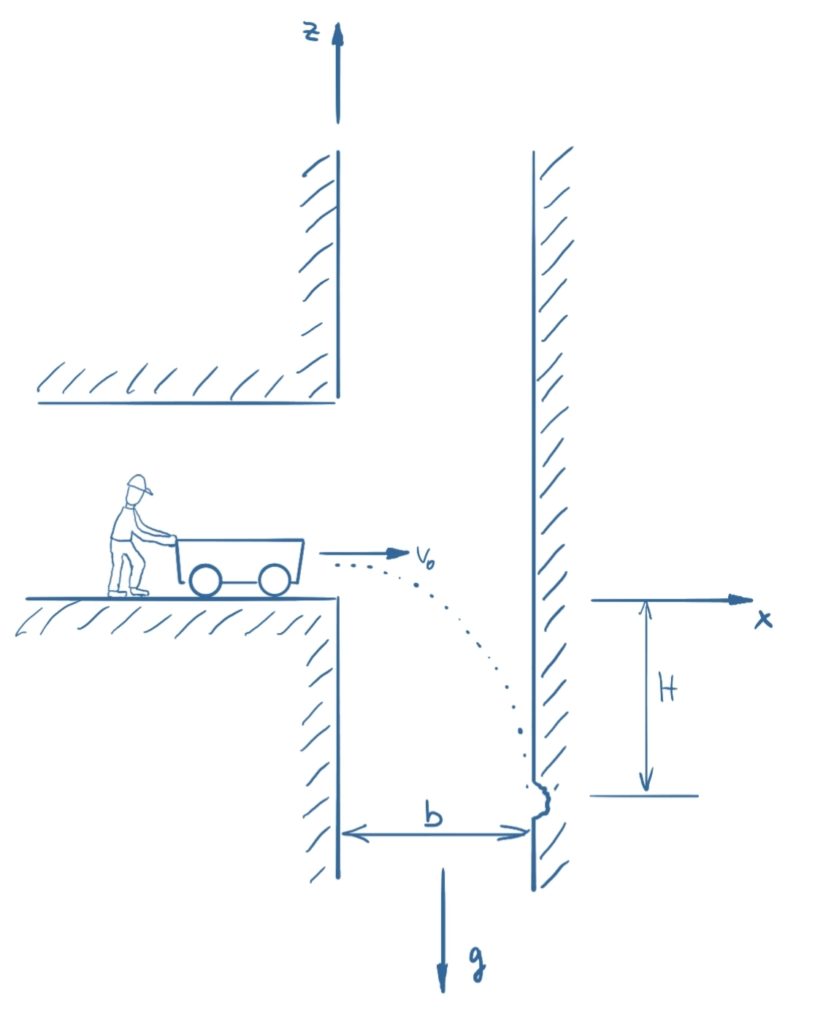
Eine Lore ist in einen Schacht gefallen und hat dabei in der Tiefe H unter der Absturzstelle Spuren an der Wand hinterlassen. Mit welcher Geschwindigkeit ist die Lore in den Schacht hinein gefahren? (Der Luftwiderstand kann vernachlässigt werden.)
Gegeben: H = 20 m, b = 4,5 m, g = 9,81 m/s²
Lösung
Ein Video mit der Lösung wird demnächst auf diesem Kanal veröffentlicht.
Die Beschleunigung beträgt
\[\tag{1} \ddot{x} = 0 \]
\[\tag{2} \ddot{z} = -g \]
Durch zweifache Integration erhält man die Funktionen in x- und z-Richtung für Geschwindigkeit und Position.
\[ \tag{3} \dot{x} = c_1 \]
\[ \tag{4} x(t) = c_1t+c_3 \]
\[ \tag{5} \dot{z}(t) = -gt + c_2 \]
\[ \tag{6} z(t) = -\frac{1}{2}gt^2 + c_2t + c_4 \]
Die Geschwindigkeit zum Zeitpunkt t = 0 beträgt
\[ \tag{7} \dot{\vec{x}}(t = 0) = v_0 \]
\[ \tag{8} \dot{\vec{z}}(t = 0) = 0 \]
womit sich c1 und c2 berechnen lassen.
\[ \require{cancel} \]\[ \tag{9} v_0 = c_1 \]
\[ \tag{10} c_1 = v_0 \]
\[ \tag{11} 0 = \bcancel{-gt} + c_2 \]
\[ \tag{12} c_2 = 0 \]
Aus den Anfangsbedingungen für die Position zum Zeitpunkt t = 0 lassen sich c3 und c4 berechnen.
\[ \require{cancel} \]\[ \tag{13} \vec{x}(t = 0) = 0 \]
\[ \tag{14} 0 = \bcancel{v_0t}+c_3 \]
\[ \tag{15} c_3 = 0 \]
\[ \tag{16} \vec{z}(t = 0) = 0 \]
\[ \tag{17} 0 = \bcancel{-\frac{1}{2}gt^2} + c_4 \]
\[ \tag{18} c_4 = 0 \]
Der bis hierhin noch unbekannte Zeitpunkt des Einschlags wird nun als T bezeichnet. Die Position der Lore zum Zeitpunkt T ist:
\[ \require{cancel} \]\[ \tag{19} \vec{x}(t = T) = b \]
\[ \tag{20} \vec{z}(t = T) = -H \]
woraus sich im Folgenden sowohl der Zeitpunkt T als auch die Anfangsgeschwindigkeit v0 berechnen lassen.
\[ \require{cancel} \]\[ \tag{21} b = v_0T \]
\[ \tag{22} -H = -\frac{1}{2}gT^2 \]
\[ \tag{23} T = \sqrt{\frac{2H}{g}} \]
\[ \tag{24} v_0 = \frac{b}{\sqrt{\frac{2H}{g}}} \]
\[ \tag{25} v_0 = \frac{ 4.5 m}{ \sqrt{ \frac{ 40 m}{ 9.81 \frac{ m }{ s^2 }}}} = 2.23 \frac{ m }{ s } \]
Hier gibt es weitere interessante Aufgaben zum Thema Kinematik.
Werbung




