Straight throw, determination of the initial speed

Task

A lorry fell into a shaft and left traces on the wall at depth H under the crash site. At what speed did the lorry go into the shaft? (The air resistance can be neglected.)

Given: H = 20 m, b = 4,5 m, g = 9,81 m/s²

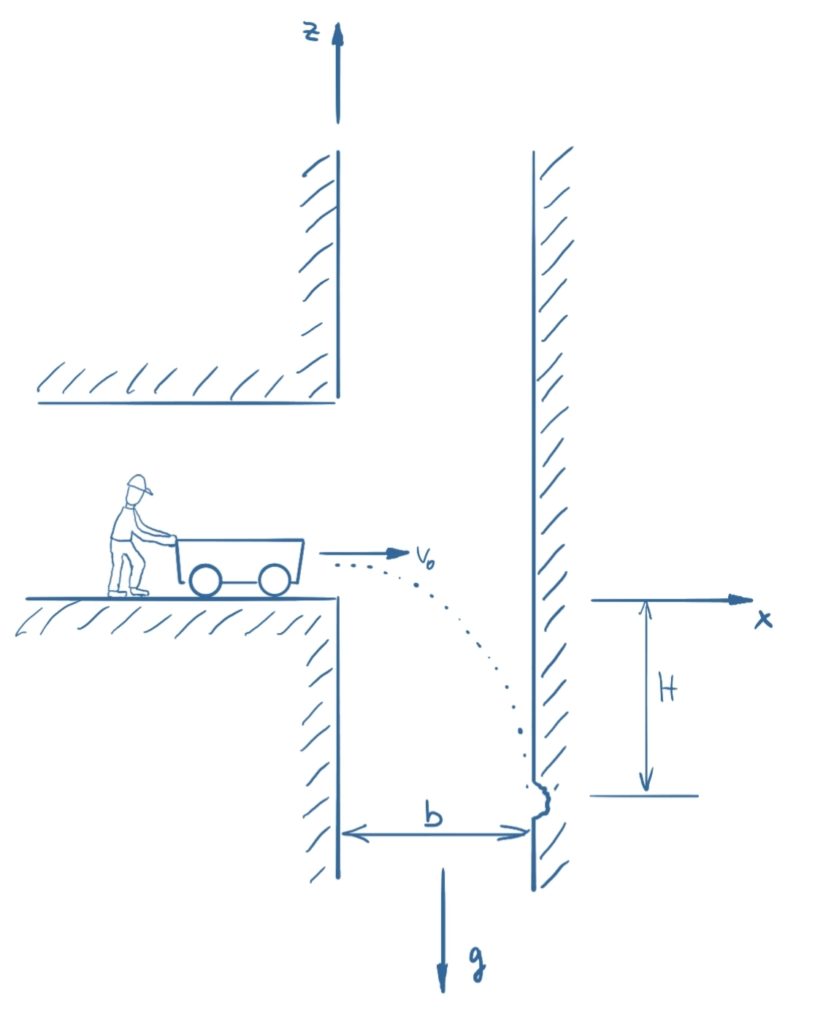
Solution

A solution video will be published soon on this channel.

The acceleration is

\[\tag{1} \ddot{x} = 0 \]

\[\tag{2} \ddot{z} = -g \]

The functions in the x and z directions for speed and position are obtained through double integration.

\[ \tag{3} \dot{x} = c_1 \]

\[ \tag{4} x(t) = c_1t+c_3 \]

\[ \tag{5} \dot{z}(t) = -gt + c_2 \]

\[ \tag{6} z(t) = -\frac{1}{2}gt^2 + c_2t + c_4 \]

The speed at time t = 0

\[ \tag{7} \dot{\vec{x}}(t = 0) = v_0 \]

\[ \tag{8} \dot{\vec{z}}(t = 0) = 0 \]

which means that c₁ and c₂ can be calculated.

\[ \require{cancel} \]

\[ \tag{9} v_0 = c_1 \]

\[ \tag{10} c_1 = v_0 \]

\[ \tag{11} 0 = \bcancel{-gt} + c_2 \]

\[ \tag{12} c_2 = 0 \]

From the initial conditions for the position at time t = 0, c₃ and c₄ can be calculated.

\[ \require{cancel} \]

\[ \tag{13} \vec{x}(t = 0) = 0 \]

\[ \tag{14} 0 = \bcancel{v_0t}+c_3 \]

\[ \tag{15} c_3 = 0 \]

\[ \tag{16} \vec{z}(t = 0) = 0 \]

\[ \tag{17} 0 = \bcancel{-\frac{1}{2}gt^2} + c_4 \]

\[ \tag{18} c_4 = 0 \]

The as yet unknown point in time of the impact is now referred to as T. The position of the cart at time T is:

\[ \require{cancel} \]

\[ \tag{19} \vec{x}(t = T) = b \]

\[ \tag{20} \vec{z}(t = T) = -H \]

From which both the time T and the initial speed v₀ can be calculated in the following.

\[ \require{cancel} \]

\[ \tag{21} b = v_0T \]

\[ \tag{22} -H = -\frac{1}{2}gT^2 \]

\[ \tag{23} T = \sqrt{\frac{2H}{g}} \]

\[ \tag{24} v_0 = \frac{b}{\sqrt{\frac{2H}{g}}} \]