Task
A gun is intended to hit an elevated target at a given angle. How big does the muzzle velocity v0 have to be? What is the minimum size of the angle for the present case? (The air resistance and the Coriolis force can be neglected.)
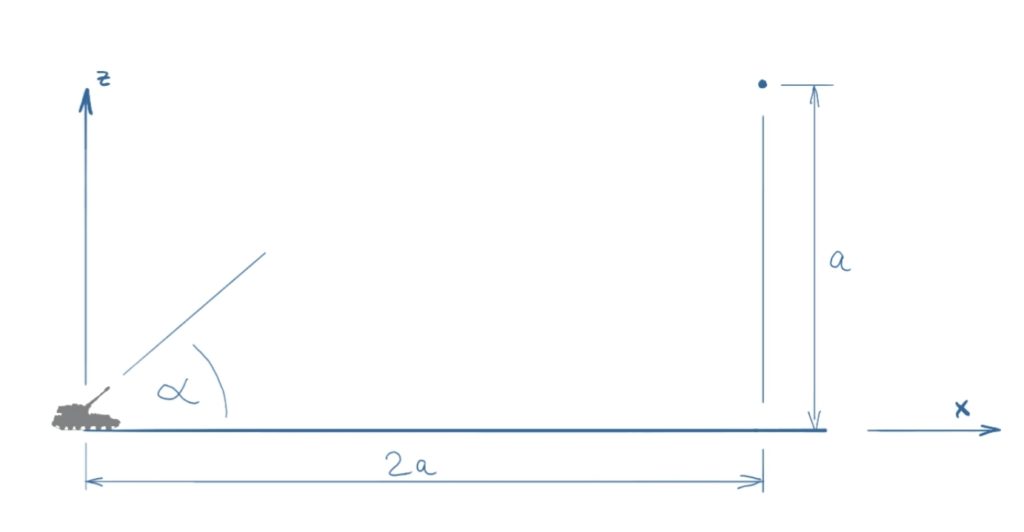
Solution
A solution video will be published soon on this channel.
The accelerations in direction x and direction y are
\[ \require{cancel} \]\[ \tag{1} \ddot{x} = 0 \]
\[ \tag{2} \ddot{z} = -g \]
The integration of both accelerations leads to the velocity
\[ \require{cancel} \]\[ \tag{3} \dot{x} = c_1 \]
\[ \tag{4} \dot{z}(t) = -gt + c_2 \]
and the location.
\[ \require{cancel} \]\[ \tag{5} x(t) = c_1t + c_3 \]
\[ \tag{6} z(t) = -\frac{1}{2}gt^2 + c_2t + c_4\]
The position of the projectile at time t = 0 in the x-direction is equal to zero, from which c3 can be calculated.
\[ \require{cancel} \]\[ \tag{7} x(t=0) = 0 \]
\[ \tag{8} 0 = \bcancel{c_1t} + c_3 \]
\[ \tag{9} c_3 = 0 \]
The z-position at time t = 0 is also zero, which results in c4.
\[ \require{cancel} \]\[ \tag{10} z(t=0) = 0 \]
\[ \tag{11} 0 = \bcancel{-\frac{1}{2}gt^2} + \bcancel{c_2t} + c_4 \]
\[ \tag{12} c_4 = 0 \]
The speed in the x direction at time t = 0 is the horizontal component of v0, which delivers c1.
\[ \require{cancel} \]\[ \tag{13} \dot{x}(t=0) = v_0 \cdot cos \alpha \]
\[ \tag{14} c_1 = v_0 \cdot cos \alpha \]
\[ \tag{15} \dot{x} = v_0 \cdot cos \alpha \]
The speed in the z-direction is the vertical component of v0, so that c2 can be determined.
\[ \require{cancel} \]\[ \tag{16} \dot{z}(t=0) = v_0 \cdot sin \alpha \]
\[ \tag{17} v_0 \cdot sin \alpha = \bcancel{-gt} + c_2 \]
\[ \tag{18} c_2 = v_0 \cdot sin \alpha \]
With the integration constants determined so far, the functions for the position of the projectile now look like this:
\[ \require{cancel} \]\[ \tag{19} x(t) = v_0 \cdot cos \alpha \cdot t \]
\[ \tag{20} z(t) = -\frac{1}{2}gt^2 + v_0 \cdot sin \alpha \cdot t\]
The time of impact is referred to as T in the following. The x position at time t = T is 2a.
\[ \require{cancel} \]\[ \tag{21} x(t=T) = 2a \]
\[ \tag{22} 2a = v_0 \cdot cos \alpha \cdot T \]
\[ \tag{23} T = \frac{2a}{v_0 \cdot cos \alpha} \]
The z-position at time T is a.
\[ \require{cancel} \]\[ \tag{24} z(t=T) = a\]
\[ \tag{25} a = -\frac{1}{2}gT^2 + v_0 \cdot sin \alpha \cdot T\]
The calculated T (equation 23) is now inserted and the equation can be solved for v0.
\[ \require{cancel} \]\[ \tag{26} a = -\frac{1}{2}g \cdot \left( \frac{2a}{v_0 \cdot cos \alpha} \right)^2 + v_0 \cdot sin \alpha \cdot \frac{2a}{v_0 \cdot cos \alpha}\]
\[ \tag{27} a = -\frac{1}{2}g \cdot \frac{4a^2}{v_0^2 \cdot cos^2 \alpha} + sin \alpha \cdot \frac{2a}{cos \alpha}\]
\[ \tag{28} a = -\frac{1}{2}g \cdot \frac{4a^2}{v_0^2 \cdot (cos(2\alpha)+1) } + 2a \cdot tan \alpha\]
\[ \tag{29} 4a \cdot tan \alpha -2a = g \cdot \frac{4a^2}{v_0^2 \cdot (cos(2\alpha)+1) } \]
\[ \tag{30} \frac{(4a \cdot tan \alpha -2a)\cdot (cos(2\alpha)+1)}{4a^2g} = \frac{1}{v_0^2 } \]
\[ \tag{31} v_0 = \sqrt{\frac{4a^2g}{(4a \cdot tan \alpha -2a)\cdot (cos(2\alpha)+1)}} \]
Determination of the minimum angle
Consider the two terms in brackets below the brackets in equation 31. If one of the two becomes zero, the equation no longer provides a solution. So it applies
\[ \require{cancel} \]\[ \tag{32} 4a \cdot tan \alpha -2a > 0 \]
\[ \tag{33} \alpha > arctan \frac{1}{2} \]
\[ \tag{34} \alpha > 26.57° \]
as
\[ \require{cancel} \]\[ \tag{35} cos(2\alpha)+1 > 0 \]
\[ \tag{36} \alpha > \frac{arccos(-1)}{2} \]
\[ \tag{37} \alpha > 180° \]
Obviously, the minimum angle is found with equation 34, while equation 37 represents the upper limit value.
Validation of the function
Below are two diagram plots with the x and y coordinates of the projectile for two different angles of fire (45 ° and 60 °) with the same parameters for distance and height. The destination is marked with a cross.
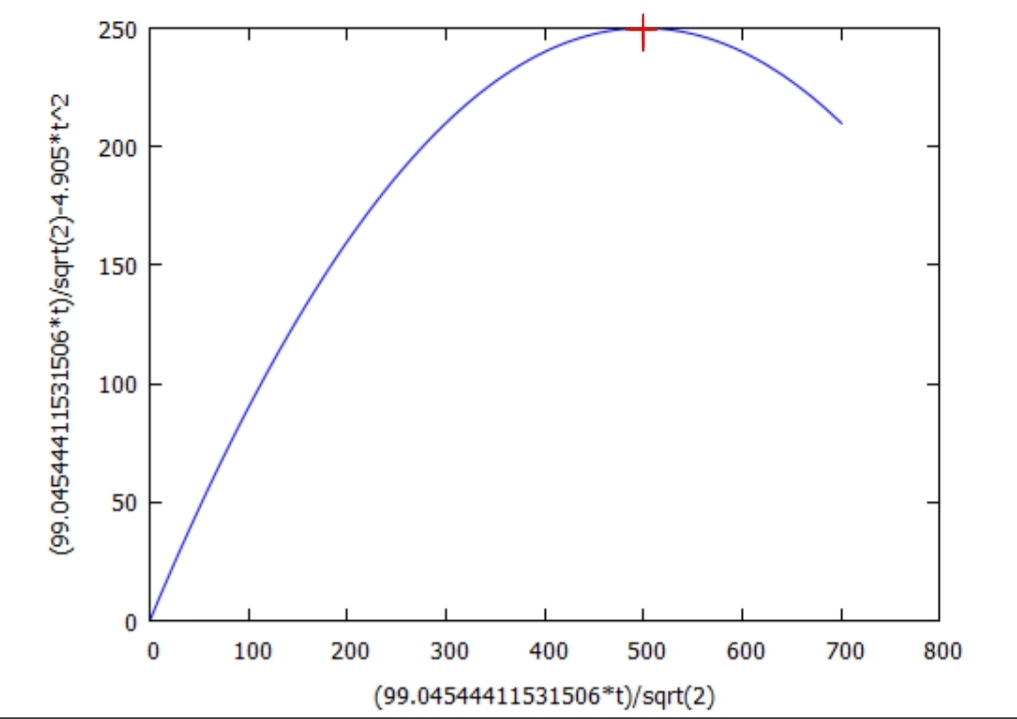
At a firing angle of 45 °, the projectile hits the target at the apex of its trajectory.
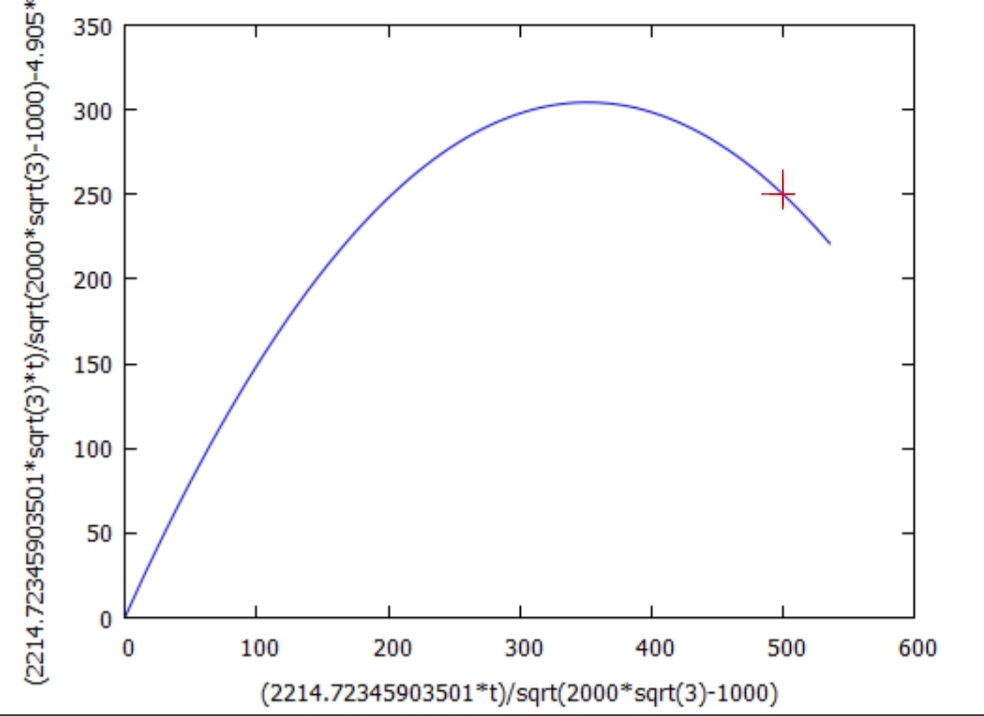
At a firing angle of 60 °, the projectile moves on a significantly elevated trajectory and hits the target in its downward movement.

