Schuss auf erhöhtes Ziel

In dieser Übung wird eine ballistische Flugbahn beim schrägen Wurf berechnet.

Aufgabe

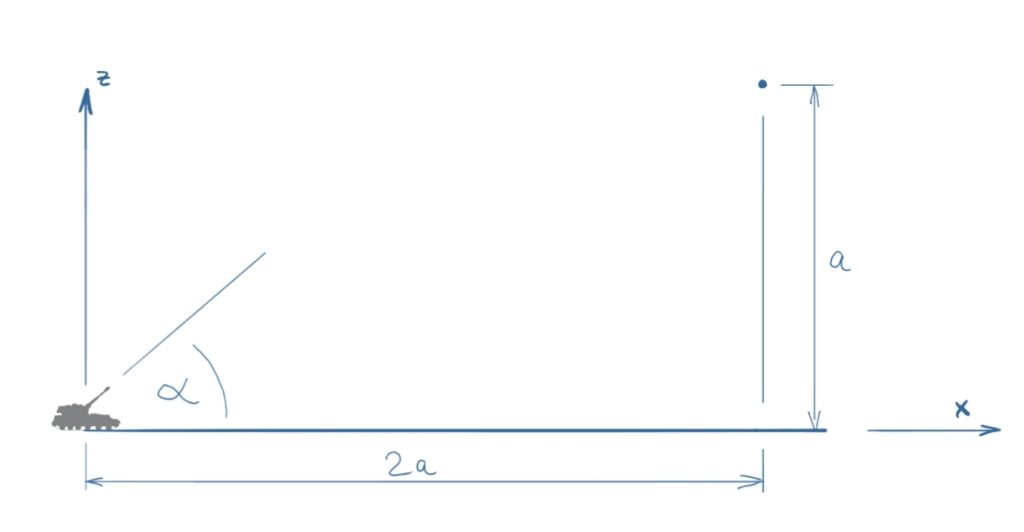
Ein Geschütz soll unter einem vorgegebenen Winkel ein erhöhtes Ziel treffen. Wie groß muss die Mündungsgeschwindigkeit sein? Wie groß muss der Winkel für den vorliegenden Fall mindestens sein? (Der Luftwiderstand soll vernachlässigt werden.)

Lösung

Ein Video mit der Lösung wird demnächst auf diesem Kanal veröffentlicht.

Die Beschleunigungen in Richtung x und y betragen

$$\require{cancel}$$

$$\tag{1} \ddot{x} = 0$$

$$\tag{2} \ddot{z} = -g$$

Durch Integration erhält man die Geschwindigkeiten

$$\require{cancel}$$

$$\tag{3} \dot{x} = c_1$$

$$\tag{4} \dot{z}(t) = -gt + c_2$$

und Positionen.

$$\require{cancel}$$

$$\tag{5} x(t) = c_1t + c_3$$

$$\tag{6} z(t) = -\frac{1}{2}gt^2 + c_2t + c_4$$

Die Position des Projektils zum Zeitpunkt t = 0 in x-Richtung ist gleich Null, woraus c₃ errechnet werden kann.

$$\require{cancel}$$

$$\tag{7} x(t=0) = 0$$

$$\tag{8} 0 = \bcancel{c_1t} + c_3$$

$$\tag{9} c_3 = 0$$

Auch die z-Position zum Zeitpunkt t = 0 ist Null, woraus sich c₄ ergibt.

$$\require{cancel}$$

$$\tag{10} z(t=0) = 0$$

$$\tag{12} c_4 = 0$$

Die Geschwindigkeit in x-Richtung zum Zeitpunkt t = 0 ist die Horizontalkomponente von v₀, woraus sich c₁ ergibt.

$$\require{cancel}$$

$$\tag{13} \dot{x}(t=0) = v_0 \cdot cos \alpha$$

$$\tag{14} c_1 = v_0 \cdot cos \alpha$$

$$\tag{15} \dot{x} = v_0 \cdot cos \alpha$$

Die Geschwindigkeit in z-Richtung ist die Vertikalkomponente von v₀, so dass c₂ bestimmt werden kann.

$$\require{cancel}$$

$$\tag{16} \dot{z}(t=0) = v_0 \cdot sin \alpha$$

$$\tag{17} v_0 \cdot sin \alpha = \bcancel{-gt} + c_2$$

$$\tag{18} c_2 = v_0 \cdot sin \alpha$$

Mit den bisher bestimmten Integrationskonstanten sehen die Funktionen für die Position des Projektils nun so aus:

$$\require{cancel}$$

$$\tag{19} x(t) = v_0 \cdot cos \alpha \cdot t$$

Der Zeitpunkt des Einschlags wird im Folgenden als T bezeichnet. Die x-Position zum Zeitpunkt t = T beträgt 2a.

$$\require{cancel}$$

$$\tag{21} x(t=T) = 2a$$

$$\tag{22} 2a = v_0 \cdot cos \alpha \cdot T$$

$$\tag{23} T = \frac{2a}{v_0 \cdot cos \alpha}$$

Die z-Position zum Zeitpunkt T beträgt a.

$$\require{cancel}$$

$$\tag{24} z(t=T) = a$$

Das errechnete T (Gleichung 23) wird nun eingesetzt und die Gleichung kann nach v₀ aufgelöst werden.

$$\require{cancel}$$

Ermittlung des minimalen Winkels

Betrachtet werden die beiden geklammerten Terme unterhalb der Klammer in Gleichung 31. Sollte einer der beiden Null werden, liefert die Gleichung keine Lösung mehr. Es gilt also

$$\require{cancel}$$

$$\tag{32} 4a \cdot tan \alpha -2a > 0$$

$$\tag{33} \alpha > arctan \frac{1}{2}$$

$$\tag{34} \alpha > 26.57°$$

sowie

$$\require{cancel}$$

$$\tag{35} cos(2\alpha)+1 > 0$$

$$\tag{36} \alpha > \frac{arccos(-1)}{2}$$

$$\tag{37} \alpha > 180°$$

Offenbar ist mit Gleichung 34 der minimale Winkel gefunden, während Gleichung 37 den oberen Grenzwert darstellt.

Validierung der Funktion

Nachfolgend werden zwei Diagrammplots mit den x- und y-Koordinaten des Projektils für zwei unterschiedliche Schusswinkel (45° und 60°) bei gleichen Parametern für Entfernung und Höhe abgebildet. Das Ziel ist mit einem Kreuz markiert.

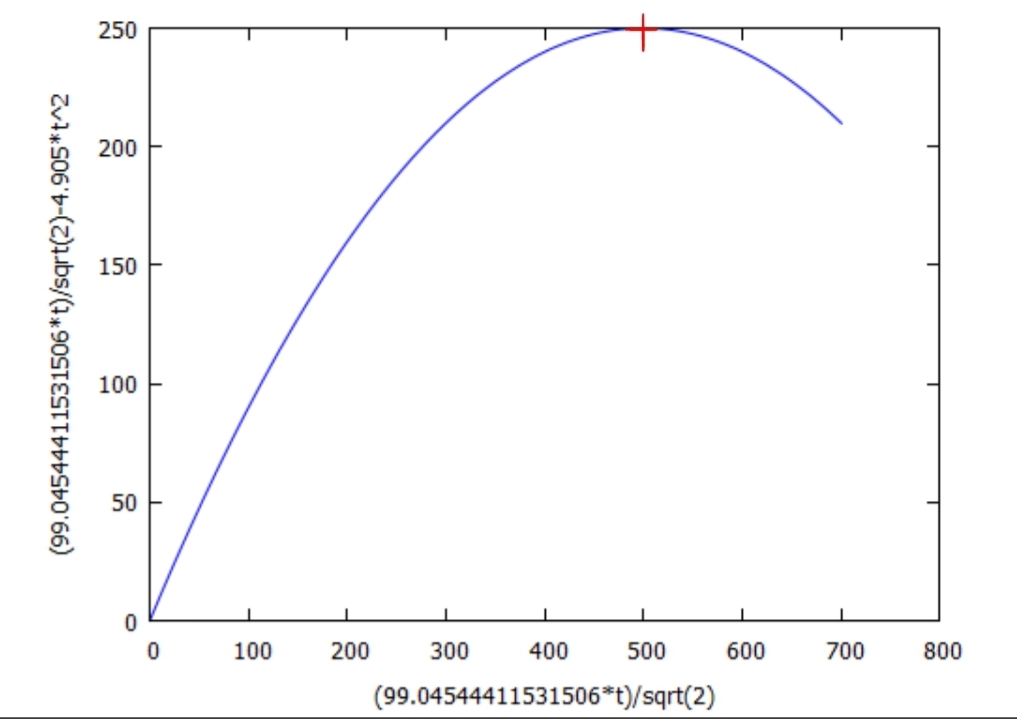
Bei einem Schusswinkel von 45° trifft das Projektil im Scheitelpunkt seiner Flugbahn das Ziel.

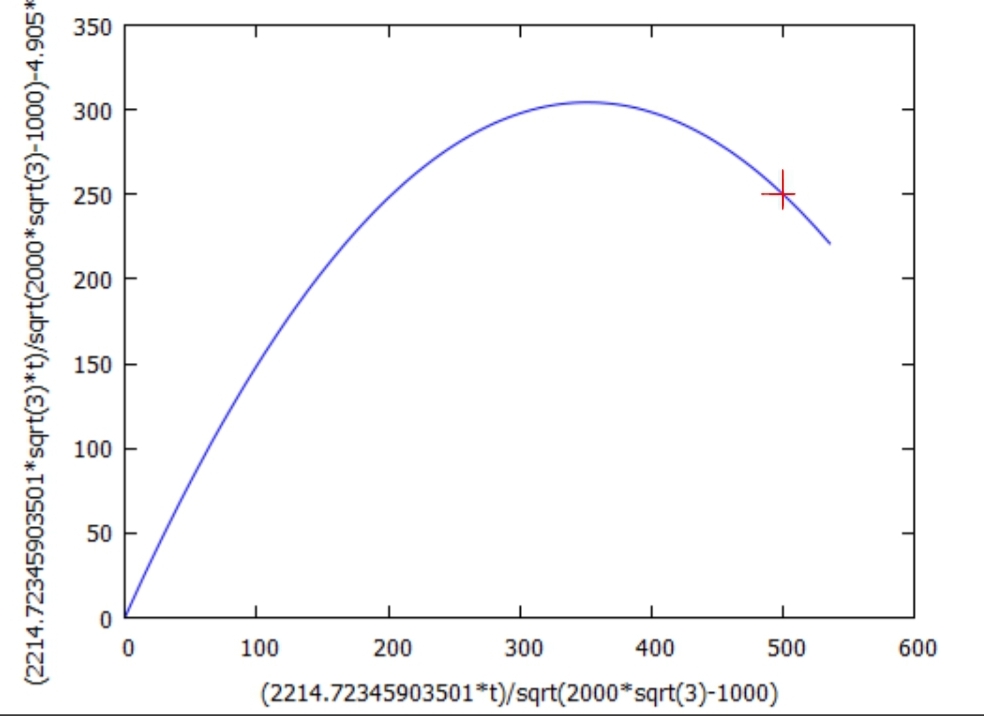
Bei einem Schusswinkel von 60° bewegt sich das Projektil auf einer deutlich überhöhten Flugbahn und trifft das Ziel in seiner Abwärtsbewegung.

Damit ist die ballistische Flugbahn beim schrägen Wurf bestimmt und validiert.

Hier gibt es weitere interessante Aufgaben mit Lösungen zur Kinematik.