Werbung
In dieser Übung aus der Aufgabensammlung Technische Mechanik II wird die Stauchung eines elastischen Körpers unter verschiedenen äußeren Zwangsbedingungen betrachtet.
Aufgabe
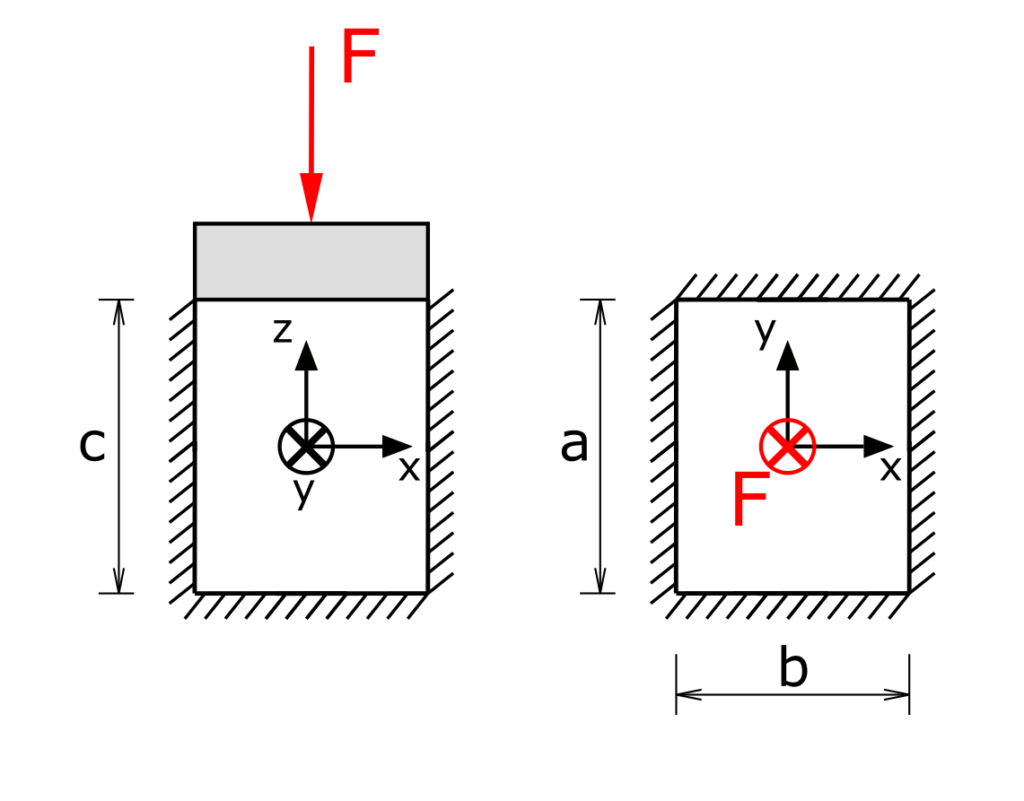
Ein elastischer Körper ist spielfrei und reibungsfrei in einem starren Gesenk eingelassen. Der Körper wird über einen starren Stempel mit der Kraft F belastet.
Gegeben:
Abmessungen a, b, c, Elastizitätsmodul E, Querkontraktionszahl ν, Dehnung θz
Gesucht:
a) Druckkraft F, um den Körper in z-Richtung um θz zu stauchen.
b) Druck auf die Flächen des Gesenkes.
c) Änderung der Konturlänge unter der Kraft F bei Wegnahme des Gesenkes.
d) Druckkraft F* bei einer Stauchung um θz ohne Gesenk.
Lösung
Das Hooke'sche Gesetz lautet:
\[ \tag{1} \epsilon_x = \frac{1}{E} \left[ \sigma_x - \nu \left( \sigma_y + \sigma_z \right) \right] \]
\[ \tag{2} \epsilon_y = \frac{1}{E} \left[ \sigma_y - \nu \left( \sigma_x + \sigma_z \right) \right] \]
\[ \tag{3} \epsilon_z = \frac{1}{E} \left[ \sigma_z - \nu \left( \sigma_x + \sigma_y \right) \right] \]
zu a)
Die Dehnungen in x- und y-Richtung sind Null.
\[ \tag{4} \epsilon_x = 0 \]
\[ \tag{5} \epsilon_y = 0 \]
Die Dehnung in z-Richtung beträgt
\[ \tag{5} \epsilon_z = - \frac{\theta_z}{c} \]
Die Spannung in z-Richtung beträgt
\[ \tag{6} \sigma_z = -\frac{F}{ab} \]
Das Hooke'sche Gesetz führt damit zu
\[ \tag{7} F = \frac{\theta_z a b E}{c \left( 1 - \frac{2 \nu^2}{1-\nu} \right)} \]
zu b)
Der Druck auf die Flächen des Gesenks beträgt
\[ \tag{8} \sigma_x = \sigma_y = -\frac{F \nu}{ab \left( 1 - \nu \right)} \]
zu c)
Bei Wegnahme des Gesenkes betragen die Spannungen
\[ \tag{9} \sigma_x = 0 \]
\[ \tag{10} \sigma_y = 0 \]
\[ \tag{11} \sigma_z = -\frac{F}{ab} \]
woraus sich die folgenden Änderungen der Konturlängen ergeben
\[ \tag{12} \Delta b = \epsilon_x b = \frac{\nu F}{Ea} \]
\[ \tag{13} \Delta a = \epsilon_y a = \frac{\nu F}{Eb} \]
\[ \tag{14} \Delta c = \epsilon_z c = -\frac{F c}{abE} \]
zu d)
Die Spannungen σx und σy sind Null. Die Dehnung ist
\[ \tag{15} \epsilon_z = -\frac{\theta_z}{c} = \frac{\sigma_z}{E} = - \frac{F^*}{abE} \]
\[ \tag{16} F^* = \frac{\theta_z E a b}{c} \]
Werbung




