Werbung
In dieser Übung aus der Aufgabensammlung Technische Mechanik II wird die thermische Dehnung eines eingespannten Körpers unter Anwendung des Hooke'schen Gesetzes betrachtet.
Aufgabe
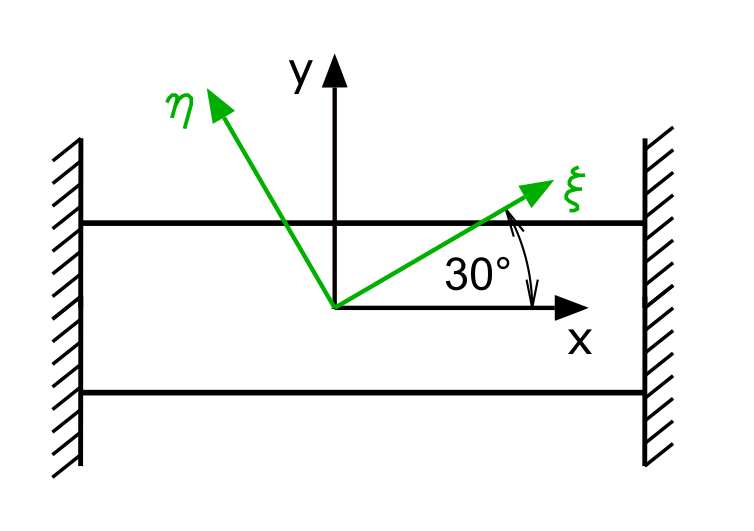
Ein elastischer Körper ist spielfrei zwischen zwei starren Wänden eingesetzt worden. Der Körper wird gleichmäßig um ΔT erwärmt.
Gegeben sind die Temperaturdifferenz ΔT, der Elastizitätsmodul E, die Querkontraktionszahl ν und der Wärmedehnungskoeffizient α.
Gesucht werden die Spannung in x-Richtung und die Dehnungen in den Richtungen η und ξ.
Lösung
Unter Berücksichtigung der thermischen Dehnung lautet das Hooke'sche Gesetz:
\[ \tag{1} \epsilon_x = \frac{1}{E} \left[ \sigma_x - \nu \left( \sigma_y + \sigma_z \right) \right] +\alpha \Delta T \]
\[ \tag{2} \epsilon_y = \frac{1}{E} \left[ \sigma_y - \nu \left( \sigma_x + \sigma_z \right) \right] +\alpha \Delta T \]
\[ \tag{3} \epsilon_z = \frac{1}{E} \left[ \sigma_z - \nu \left( \sigma_x + \sigma_y \right) \right] +\alpha \Delta T \]
Die Dehnung in x-Richtung ist Null, da der Körper eingespannt ist.
\[ \tag{4} 0 = \frac{1}{E} \left[ \sigma_x - \nu \left( \sigma_y + \sigma_z \right) \right] +\alpha \Delta T \]
Die Spannungen in y- und z-Richtung sind Null, da sich der Körper in diese Richtungen frei ausdehnen kann.
\[ \tag{5} \sigma_y = 0 \]
\[ \tag{6} \sigma_z = 0 \]
Eingesetzt in die ersten drei Gleichungen führt dies zu
\[ \tag{7} \sigma_x=-E \Delta T \alpha \]
\[ \tag{8} \epsilon_y= \Delta T \alpha \left(1+\nu \right) \]
\[ \tag{9} \epsilon_z= \Delta T \alpha \left(1+\nu \right) \]
Die Drehung ins ξ-η-Koordinatensystem beträgt 30°. Die Winkelfunktionen ergeben für diesen Winkel charakteristische Ergebnisse, so dass sich folgende Dehnungen einstellen:
\[ \tag{10} \epsilon_\xi= 2\Delta T \alpha \left(1+\nu \right) \]
\[ \tag{11} \epsilon_\eta= \frac{2}{\sqrt{3}}\Delta T \alpha \left(1+\nu \right) \]
Werbung




