In this exercise, the thermal expansion of a restrained body is considered using Hooke's law.
Task
An elastic body has been inserted between two rigid walls without clearance. The body is heated evenly by ΔT.
The temperature difference ΔT, the Young's modulus of elasticity E, the Poisson's ratio ν and the coefficient of thermal expansion α are given.
We are looking for the stress in the x direction and the strain in the directions η and ξ.
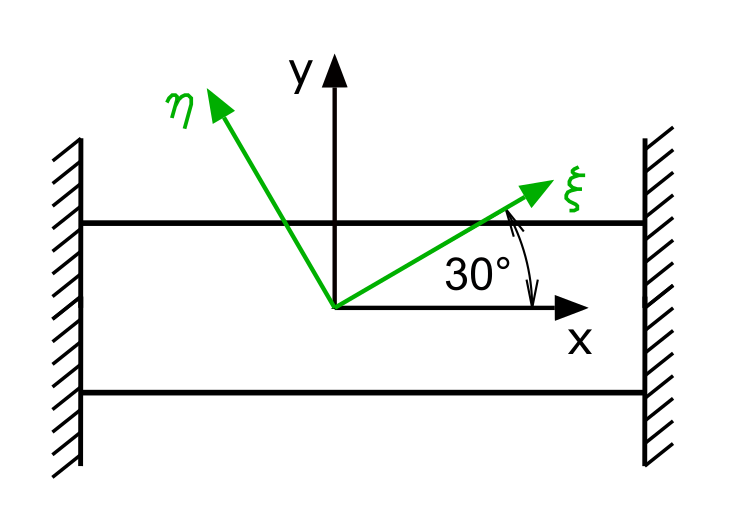
Solution
Taking into account the thermal expansion, Hooke's law reads:
\[ \tag{1} \epsilon_x = \frac{1}{E} \left[ \sigma_x - \nu \left( \sigma_y + \sigma_z \right) \right] +\alpha \Delta T \]
\[ \tag{2} \epsilon_y = \frac{1}{E} \left[ \sigma_y - \nu \left( \sigma_x + \sigma_z \right) \right] +\alpha \Delta T \]
\[ \tag{3} \epsilon_z = \frac{1}{E} \left[ \sigma_z - \nu \left( \sigma_x + \sigma_y \right) \right] +\alpha \Delta T \]
The strain in the x-direction is zero because the body is clamped.
\[ \tag{4} 0 = \frac{1}{E} \left[ \sigma_x - \nu \left( \sigma_y + \sigma_z \right) \right] +\alpha \Delta T \]
The stresses in the y and z directions are zero, as the body can expand freely in these directions.
\[ \tag{5} \sigma_y = 0 \]
\[ \tag{6} \sigma_z = 0 \]
Used in the first three equations, this leads to
\[ \tag{7} \sigma_x=-E \Delta T \alpha \]
\[ \tag{8} \epsilon_y= \Delta T \alpha \left(1+\nu \right) \]
\[ \tag{9} \epsilon_z= \Delta T \alpha \left(1+\nu \right) \]
The rotation in the ξ-η coordinate system is 30 °. The trigonometric functions give characteristic results for this angle, so that the following expansions occur:
\[ \tag{10} \epsilon_\xi= 2\Delta T \alpha \left(1+\nu \right) \]
\[ \tag{11} \epsilon_\eta= \frac{2}{\sqrt{3}}\Delta T \alpha \left(1+\nu \right) \]

