In this exercise the compression of an elastic body under different external constraints is considered.
Task
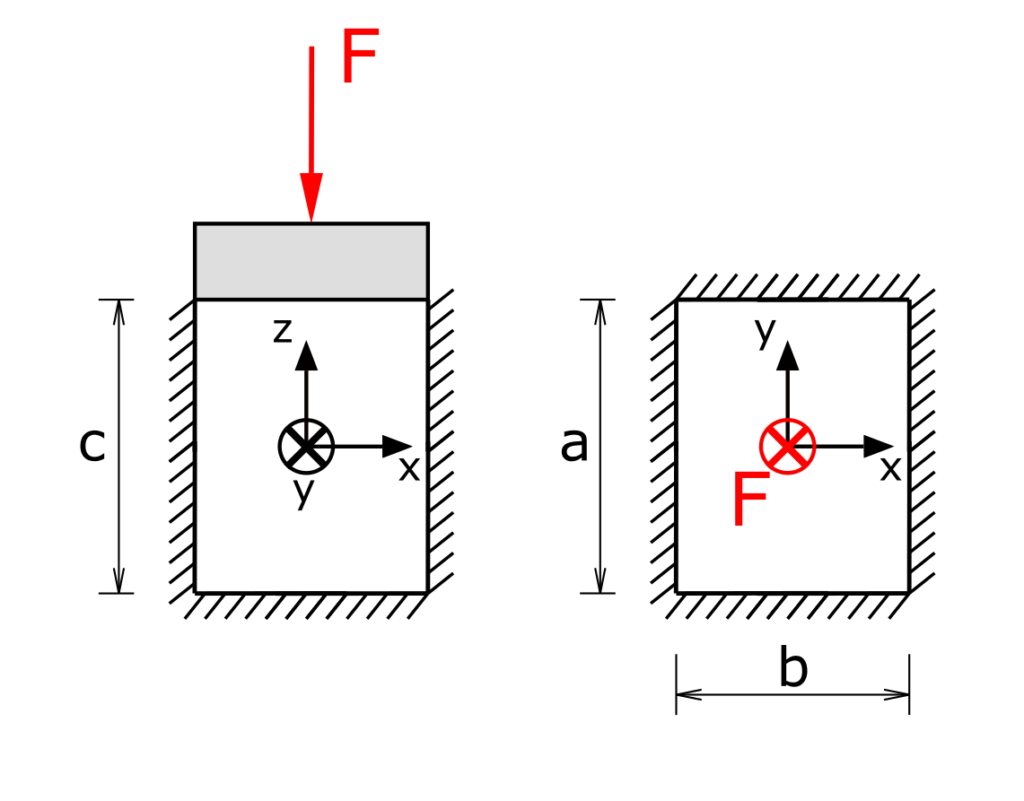
An elastic body is embedded in a rigid die without clearance and without friction. The body is loaded with the force F via a rigid plunger.
Given parameters:
Dimensions a, b, c, Young's modulus E, Poisson's ratio ν, strain θz
To be determined:
a) Compression force F to compress the body in the z-direction by θz.
b) Pressure on the surfaces of the die.
c) Change of the contour length under the force F when the die is removed.
d) Compression force F * with a compression by θz without a die.
Solution
Hooke's law is:
\[ \tag{1} \epsilon_x = \frac{1}{E} \left[ \sigma_x - \nu \left( \sigma_y + \sigma_z \right) \right] \]
\[ \tag{2} \epsilon_y = \frac{1}{E} \left[ \sigma_y - \nu \left( \sigma_x + \sigma_z \right) \right] \]
\[ \tag{3} \epsilon_z = \frac{1}{E} \left[ \sigma_z - \nu \left( \sigma_x + \sigma_y \right) \right] \]
reg. a)
The strains in direction x and y are Zero.
\[ \tag{4} \epsilon_x = 0 \]
\[ \tag{5} \epsilon_y = 0 \]
The strain in z-direction is
\[ \tag{5} \epsilon_z = - \frac{\theta_z}{c} \]
The tension in z-direction is
\[ \tag{6} \sigma_z = -\frac{F}{ab} \]
With this Hooke's law leads to
\[ \tag{7} F = \frac{\theta_z a b E}{c \left( 1 - \frac{2 \nu^2}{1-\nu} \right)} \]
reg. b)
The pressure at the surfaces of the die is
\[ \tag{8} \sigma_x = \sigma_y = -\frac{F \nu}{ab \left( 1 - \nu \right)} \]
reg. c)
When the die is removed, the tensions are
\[ \tag{9} \sigma_x = 0 \]
\[ \tag{10} \sigma_y = 0 \]
\[ \tag{11} \sigma_z = -\frac{F}{ab} \]
from which the following changes in the contour lengths result
\[ \tag{12} \Delta b = \epsilon_x b = \frac{\nu F}{Ea} \]
\[ \tag{13} \Delta a = \epsilon_y a = \frac{\nu F}{Eb} \]
\[ \tag{14} \Delta c = \epsilon_z c = -\frac{F c}{abE} \]
reg. d)
The stresses σx and σy are zero. The strain is
\[ \tag{15} \epsilon_z = -\frac{\theta_z}{c} = \frac{\sigma_z}{E} = - \frac{F^*}{abE} \]
\[ \tag{16} F^* = \frac{\theta_z E a b}{c} \]

