Werbung
Diese Übung behandelt folgende Fragen:
- Welches Moment entsteht, wenn eine Kraft parallel zu ihrer Wirkrichtung verschoben wird?
- Wie kann man das Moment für eine schräg angreifende Kraft berechnen?
- Wie berechnet man den Hebelarm einer angreifenden Kraft?
Aufgabe
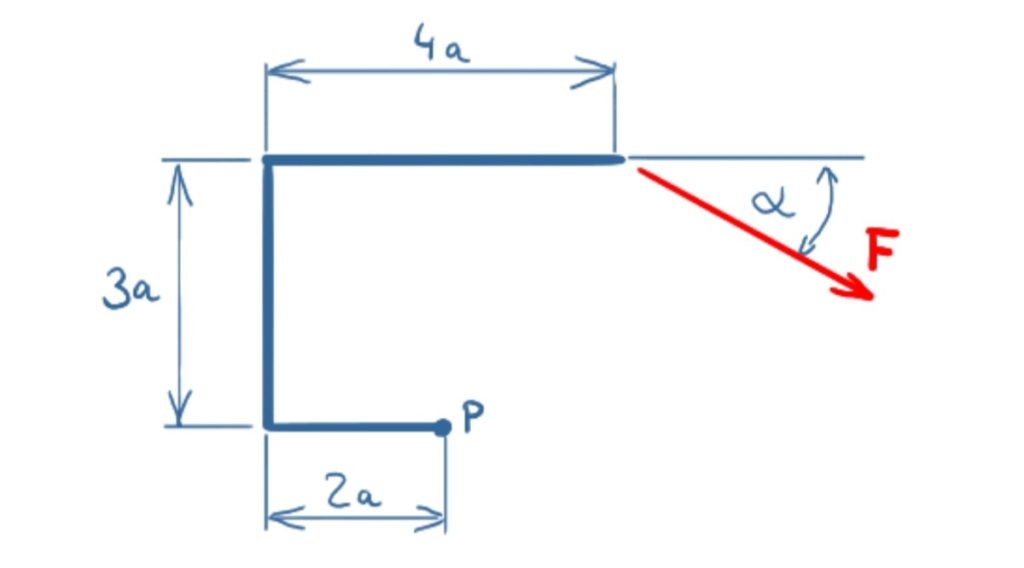
Die Kraft F soll in den Punkt P verschoben werden. Welches Moment entsteht dabei?
Lösung
Das nachfolgende Video zeigt die Lösungsvariante 1.
Durch das Verschieben einer Kraft parallel zu ihrer Wirkrichtung entsteht ein Moment, auch Versatzmoment genannt. Der Hebelarm des Moments ist der Betrag der Verschiebung.
Lösungsvariante 1
In der Variante 1 wird ohne Kräftezerlegung gerechnet. Sie ist aufwändiger als Variante 2.
Lösungsskizze
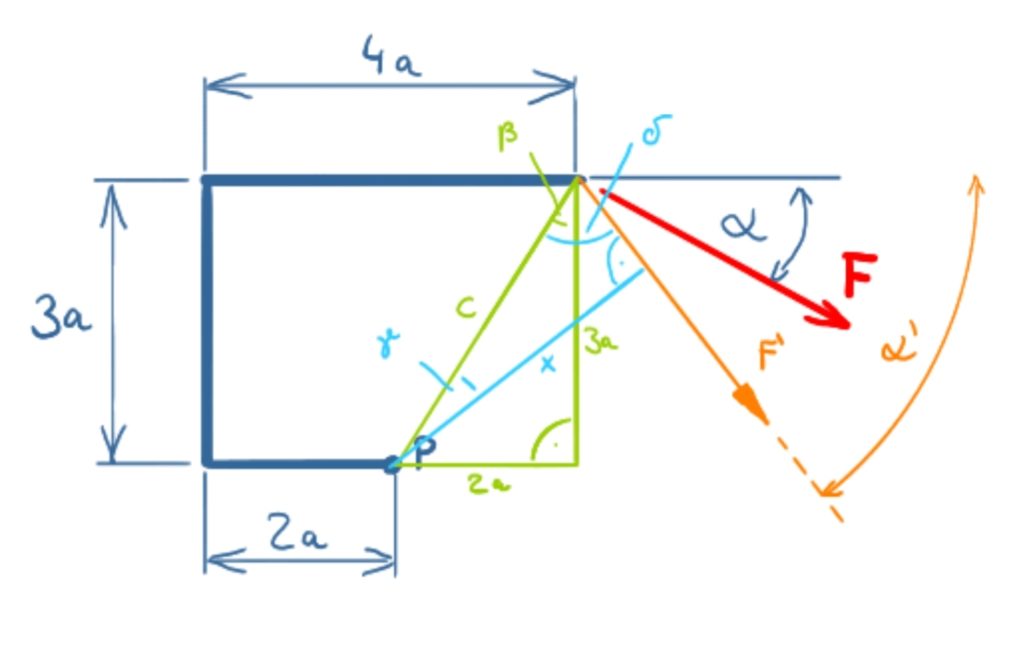
Die Art, wie die Skizze zu der Aufgabe ausgeführt ist, legt nahe, dass man direkt über den Satz des Pythagoras und die Kantenlängen 3a und 4a-2a = 2a den Hebelarm für die Kraft F berechnen kann. Das ist aber ein Trugschluss, denn sobald man die Skizze für einen geänderten Winkel anfertigt, ist zu erkennen, dass der Hebelarm wie in der nachfolgenden Skizze ermittelt werden muss.
Lösungsweg
\[ \require{cancel} \]Da die Lösung für einen beliebigen Winkel α gefunden werden soll, wurde zur Verdeutlichung der geometrischen Verhältnisse in der oben gezeigten Lösungsskizze die Kraft F' und α' eingetragen. In den nachfolgenden Formeln werden jedoch die Werte F und α verwendet. In der hier beschriebenen Lösung wurden rechtsdrehende Momente als positiv definiert (im Lösungsvideo wurden linksdrehende Momenta als positiv angenommen). Das Moment in Punkt P berechnet sich aus
\[\tag{1} M_P = F \cdot x \]
Der Hebelarm x ergibt sich aus
\[\tag{2} x = c \cdot \cos \gamma \]
Die Seite c kann über den Satz des Pythagoras berechnet werden.
\[\tag{3} c = \sqrt{3^2a^2+2^2a^2} \]
\[\tag{4} c = \sqrt{13}a \]
Die Winkel hängen wie folgt zusammen:
\[\tag{5} \gamma = 90° - \delta \]
\[\tag{6} \delta = 90° - \alpha + \beta \]
\[\tag{7} \beta = arctan \left( \frac{2\bcancel{a}}{3\bcancel{a}} \right) = 33.7° \]
\[\tag{8} \delta = 123.7° - \alpha \]
\[\tag{9} \gamma = \alpha - 33.7° \]
Somit kann der Hebelarm x bestimmt werden
\[\tag{10} x = \sqrt{13}a \cdot \cos (\alpha - 33.7°) \]
Und letztendlich auch das resultierende Moment
\[\tag{11} M_P = F \cdot \sqrt{13}a \cdot \cos (\alpha - 33.7°) \]
Das Moment für eine schräg angreifende Kraft kann auch durch Zerlegung der Kraft in ihre Komponenten berechnet werden.
Lösungsvariante 2
In dieser Lösung wird ein x-y-Koordinatensystem zugrunde gelegt und die Kräfte in ihre Komponenten zerlegt. Rechtsdrehende Momente sind wieder positiv. Die beiden Komponenten der angreifenden Kraft F sind:
\[\tag{1} F_x = F \cdot cos \alpha \]
\[\tag{2} F_y = F \cdot sin \alpha \]
Das resultierende Moment folgt aus:
\[\tag{3} M_P = F \cdot cos \alpha \cdot 3a + F \cdot sin \alpha \cdot 2a \]
\[\tag{4} M_P = F \cdot a \cdot (3 \cdot cos \alpha + 2 \cdot sin \alpha) \]
Die zweite Lösungsvariante ist damit wesentlich einfacher als die erste.
Hier gibt es weitere Aufgaben zum Thema "resultierende Momente berechnen".
Werbung




