Werbung
Diese Übung behandelt folgende Fragen:
- Wie berechnet man ein resultierendes Moment?
- Wie bildet man das Kreuzprodukt von Ortsvektor und Kraftvektor?
- Wie wendet man die Sarrus-Regel an?
Hier gibt es weitere Aufgaben zur Berechnung resultierender Momente, auch ohne Vektorrechnung und Sarrus-Regel.
Aufgabe
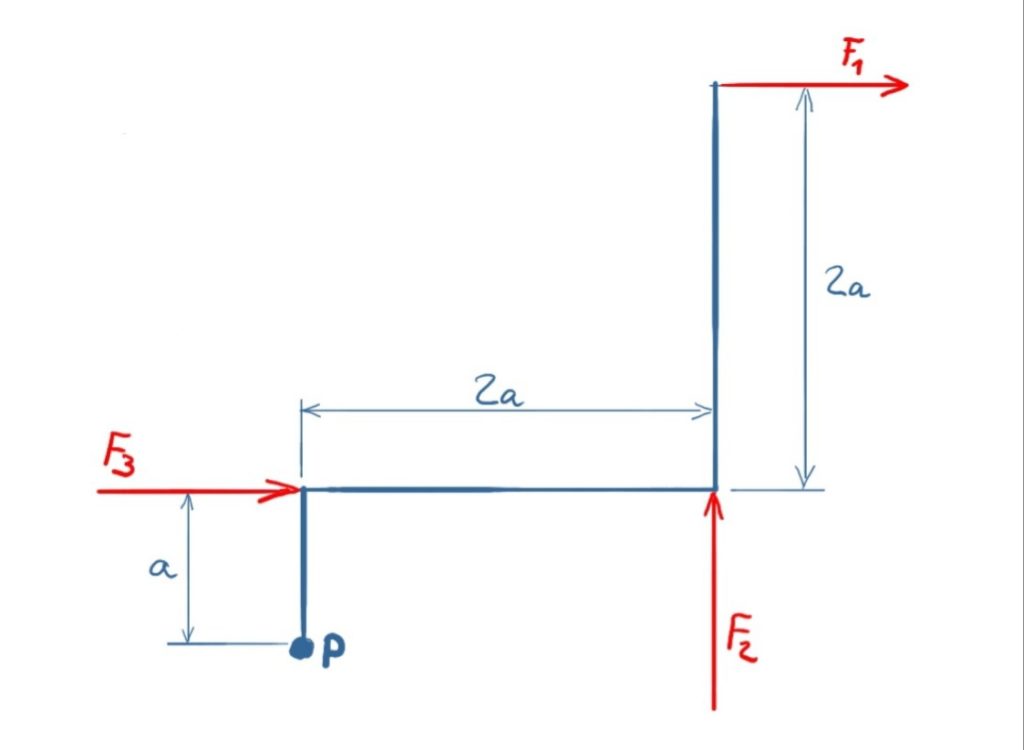
An einem Rahmen greifen die Kräfte F1, F2 und F3 an. Welches resultierende Moment entsteht in Punkt P?
geg.: F1 = F2 = 2F, F3 = F
Lösung
In der dargestellten Lösung wird das resultierende Moment mit dem Kreuzprodukt ermittelt. Damit die Sarrus-Regel zur Berechnung angewendet werden kann, werden die Ortsvektoren und die Kraftvektoren jeweils um die z-Koordinate ergänzt, auch wenn es sich hier um ein ebenes Problem handelt.
Die Koordinatenrichtung ist y nach oben, x nach rechts.
Das resultierende Moment ergibt sich nach folgender Gleichung aus den Kreuzprodukten der Kraftvektoren mit ihren jeweiligen Ortsvektoren.
\[ \require{cancel} \] \[ \newcommand{\myvec}[1]{{\begin{pmatrix}#1\end{pmatrix}}} \]\[\tag{1} \vec{M(P)} = \sum_{i=1}^3 \vec{r_i} \times \vec{F_i} \]
Die Kraftvektoren lauten
\[\tag{2} \vec{F_1} = \myvec{2F\\0\\0} \]
\[\tag{3} \vec{F_2} = \myvec{0\\2F\\0} \]
\[\tag{4} \vec{F_3} = \myvec{F\\0\\0} \]
Die Ortsvektoren lauten
\[\tag{5} \vec{r_1} = \myvec{2a\\3a\\0} \]
\[\tag{6} \vec{r_2} = \myvec{2a\\a\\0} \]
\[\tag{7} \vec{r_3} = \myvec{0\\a\\0} \]
Die detaillierte Vorgehensweise zur Berechnung des Kreuzprodukts mit der Sarrus-Regel ist im oben aufgeführten Lösungsvideo beschrieben. Das resultierende Moment ergibt sich zu
\[\tag{8} \vec{M(P)} = \vec{r_1} \times \vec{F_1} + \vec{r_2} \times \vec{F_2} + \vec{r_3} \times \vec{F_3} \]
\[\tag{9} \vec{M(P)} = \myvec{2a\\3a\\0} \times \myvec{2F\\0\\0} + \myvec{2a\\a\\0} \times \myvec{0\\2F\\0} + \myvec{0\\a\\0} \times \myvec{F\\0\\0} \]
\[\tag{10} \vec{M(P)} = \myvec{0\\0\\-6Fa} + \myvec{0\\0\\4Fa} + \myvec{0\\0\\-Fa} = \myvec{0\\0\\-3Fa}\]
Werbung




