This exercise is about the following questions:
- How to calculate the resulting moment?
- How to calculate the cross product of location vector and force vector?
- How to apply the rule of Sarrus?
If you are looking for the calculation of resulting moments without vectors and the rule of sarrus, take a look into our other exercises about moments.
Task
The forces F1, F2 and F3 are acting on a frame. Which moment results in point P?
given: F1 = F2 = 2F, F3 = F
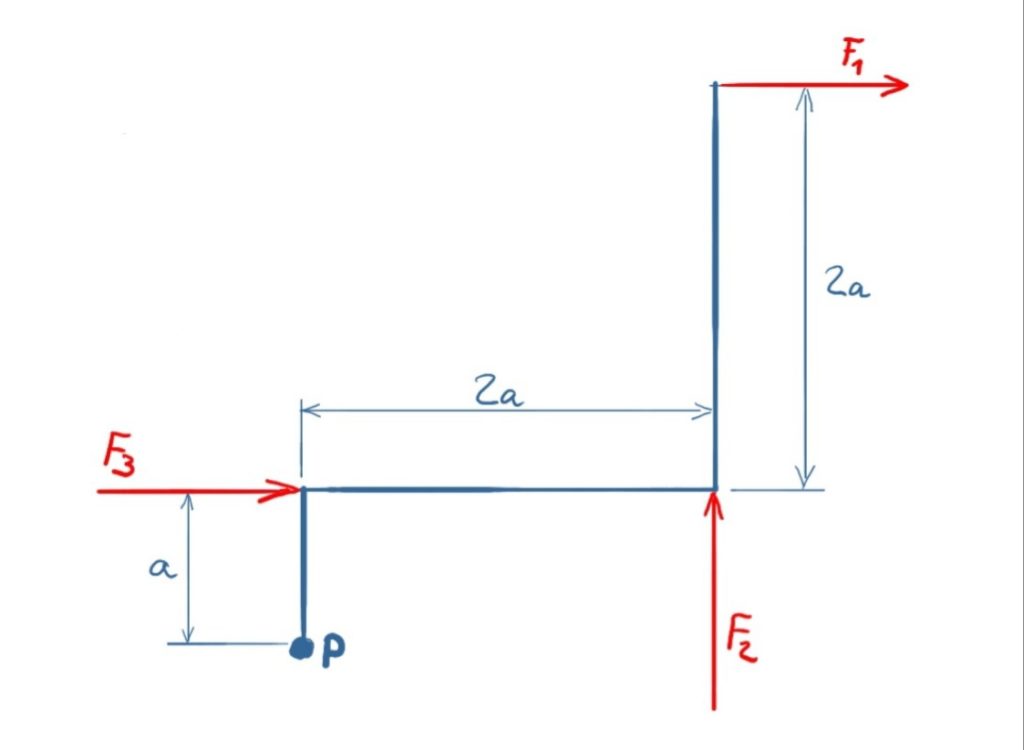
Solution
The following video is in german language.
In the solution shown, the resulting moment is determined using the cross product. For the Sarrus rule to be applied for the calculation, the position vectors and the force vectors are each supplemented by the z-coordinate, even if this is a flat problem.
The coordinate direction is y upwards, x to the right.
The moment in point P results from the following equation: the sum of moments is the sum of the cross products of each force vector with its respective position vector.
\[ \require{cancel} \] \[ \newcommand{\myvec}[1]{{\begin{pmatrix}#1\end{pmatrix}}} \]\[\tag{1} \vec{M(P)} = \sum_{i=1}^3 \vec{r_i} \times \vec{F_i} \]
The force vectors are
\[\tag{2} \vec{F_1} = \myvec{2F\\0\\0} \]
\[\tag{3} \vec{F_2} = \myvec{0\\2F\\0} \]
\[\tag{4} \vec{F_3} = \myvec{F\\0\\0} \]
The position vectors are
\[\tag{5} \vec{r_1} = \myvec{2a\\3a\\0} \]
\[\tag{6} \vec{r_2} = \myvec{2a\\a\\0} \]
\[\tag{7} \vec{r_3} = \myvec{0\\a\\0} \]
The detailed procedure for calculating the cross product with the Sarrus rule is described in the solution video above. The resulting moment is
\[\tag{8} \vec{M(P)} = \vec{r_1} \times \vec{F_1} + \vec{r_2} \times \vec{F_2} + \vec{r_3} \times \vec{F_3} \]
\[\tag{9} \vec{M(P)} = \myvec{2a\\3a\\0} \times \myvec{2F\\0\\0} + \myvec{2a\\a\\0} \times \myvec{0\\2F\\0} + \myvec{0\\a\\0} \times \myvec{F\\0\\0} \]
\[\tag{10} \vec{M(P)} = \myvec{0\\0\\-6Fa} + \myvec{0\\0\\4Fa} + \myvec{0\\0\\-Fa} = \myvec{0\\0\\-3Fa}\]

