Werbung
Diese Übung befasst sich sich mit den Schnittgrößen eines überstehenden Trägers und behandelt folgende Fragen:
- Wie ermittelt man die Schnittgrößen eines Trägers, der mit Einzellasten belastet wird?
- Wie berechnet man die Funktion für das Biegemoment eines Trägers?
- An welchen Stellen teilt man einen Träger in verschiedene Bereiche ein?
Aufgabe
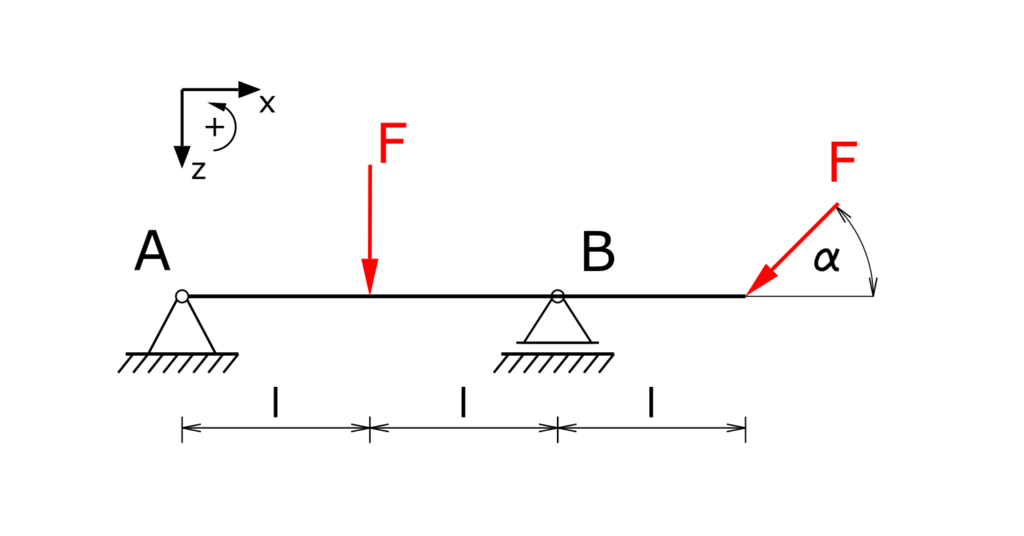
Ein Träger mit einem überstehenden Ende ist auf zwei Stützen gelagert und wird durch die Kraft F einmal vertikal und unter einem Winkel angreifend belastet. Der Träger ist in Lager B durchgehend. Zu ermitteln sind die Lagerreaktionen und die Beanspruchungsgrößen!
Lösung
Der Träger wird freigeschnitten und die Lagerreaktionen werden angetragen. Linksdrehende Momente werden positiv angenommen. Zu beachten ist die abwärts gerichtete z-Achse!
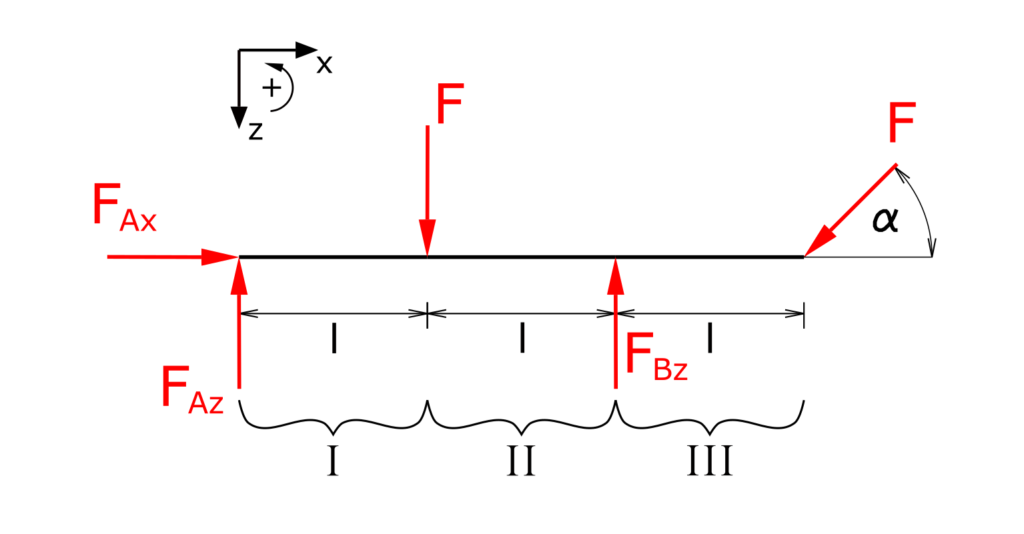
Ermittlung der Lagerreaktionen
Aufstellen der Gleichgewichtsbedingungen für Kräfte in x- und z-Richtung sowie für die Momente:
\[ \tag{1} \sum F_x = 0 = F_{Ax} - F \cdot cos \alpha\]
\[ \tag{2} \sum F_z = 0 = - F_{Az} +F -F_{Bz} + F \cdot sin \alpha \]
\[ \tag{3} \sum M(A) = 0 = -F\cdot l +F_{Bz} \cdot 2 l - F \cdot sin \alpha \cdot 3 l \]
Damit kann FBz unmittelbar bestimmt werden.
\[ \tag{4} F_{Bz} =F \cdot \frac{ 1 + 3 \cdot sin \alpha }{2} \]
Anschließend werden die ersten beiden Gleichungen nach FAx bzw. FAz aufgelöst.
\[ \tag{5} F_{Ax} = F \cdot cos \alpha\]
\[ \tag{6} F_{Az} = F - F \cdot \frac{ 1 + 3 \cdot sin \alpha }{2} + F \cdot sin \alpha \]
\[ \tag{7} F_{Az} = \frac{F}{2} \cdot \left( 1 - sin \alpha \right) \]
Ermittlung der Schnittgrößen
Es ist günstig, die Schnittrichtung in den jeweiligen Abschnitten bzw. Bereichen so zu wählen, dass die Gleichungen möglichst einfach gehalten werden können. In diesem Fall bedeutet das, dass der erste Bereich rechts abgeschnitten wird, die beiden folgenden Bereiche werden links abgeschnitten. Die jeweils betrachteten Abschnitte sind zur Verdeutlichung grün markiert. Im Folgenden werden Normalkräfte mit N, Querkräfte mit Q und das Biegemoment mit Mb bezeichnet.
Bereich I
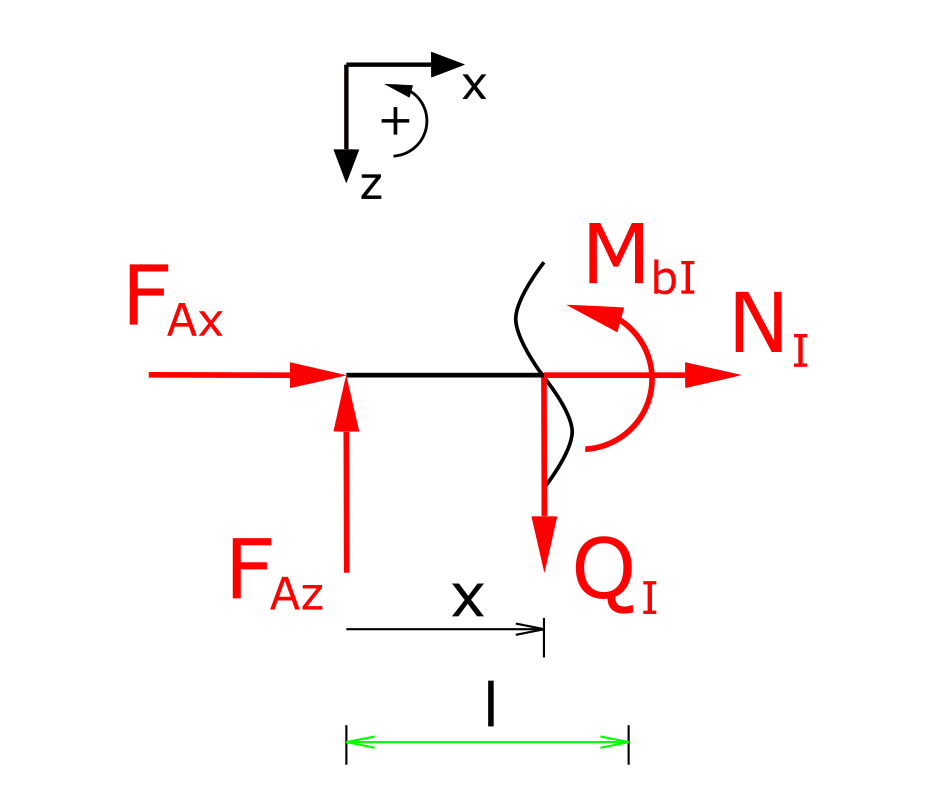
Aufstellen der Gleichgewichtsbedingungen für Kräfte in z-Richtung sowie für die Momente:
\[ \tag{8} \sum F_x = 0 = F_{Ax} + N_I \]
\[ \tag{9} \sum F_z = 0 = -F_{Az} + Q_I \]
\[ \tag{10} \sum M(x) = 0 = -F_{Az} \cdot x + M_{bI} \]
Die berechneten Lagerkräfte werden nun eingesetzt:
\[ \tag{11} N_I = - F \cdot cos \alpha \]
\[ \tag{12} Q_I = \frac{F}{2} \cdot \left( 1 - sin \alpha \right) \]
\[ \tag{13} M_{bI} = \frac{F}{2} \cdot \left( 1 - sin \alpha \right) \cdot x \]
Bereich II
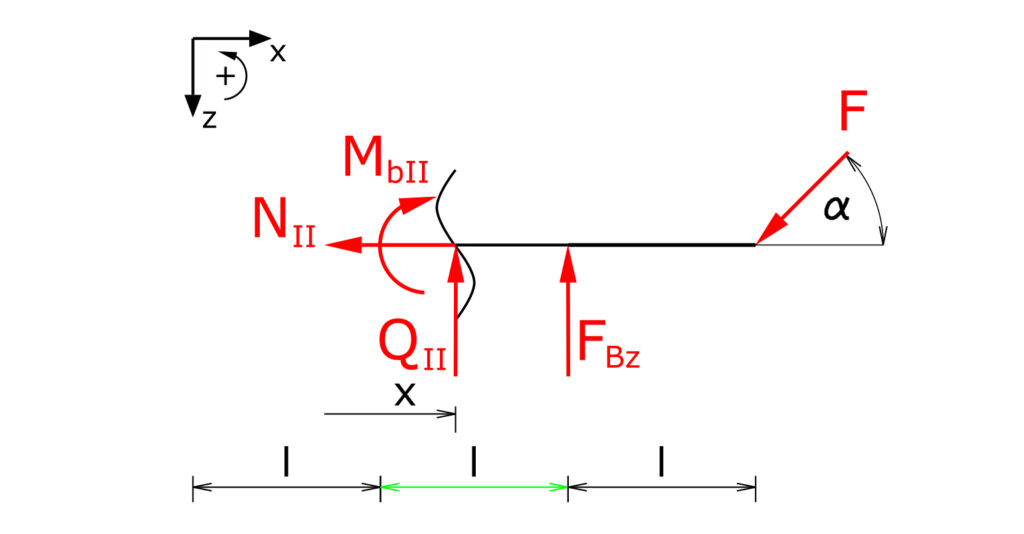
Dieser Bereich wird entgegengesetzt zu Bereich I betrachtet. D.h. die Schnittkräfte werden hier entsprechend negativ angetragen.
Aufstellen der Gleichgewichtsbedingungen für Kräfte in z-Richtung sowie für die Momente:
\[ \tag{14} \sum F_x = 0 = -N_{II} - F \cdot cos \alpha \]
\[ \tag{15} \sum F_z = 0 = -Q_{II} - F_{Bz} + F \cdot sin \alpha \]
\[ \tag{16} \sum M(x) = 0 = -M_{bII} + F_{Bz} \cdot (2l-x) - F \cdot sin \alpha \cdot (3l-x) \]
Die bereits bekannte Lagerkraft FBz wird nun eingesetzt, so dass alle Schnittgrößen in Bereich II bestimmt werden können:
\[ \tag{17} N_{II} = F \cdot cos \alpha \]
\[ \tag{18} Q_{II} = - F \cdot \frac{ 1 + 3 \cdot sin \alpha }{2} + F \cdot sin \alpha \]
\[ \tag{19} Q_{II} = - \frac{F}{2} \cdot (1 + sin \alpha) \]
\[ \tag{20} M_{bII} = F \cdot \frac{ 1 + 3 \cdot sin \alpha }{2} \cdot (2l-x) - F \cdot sin \alpha \cdot (3l-x) \]
\[ \tag{21} M_{bII} = \frac{F}{2} \cdot \left( 2l - x - \sin \alpha\cdot x \right) \]
Bereich III
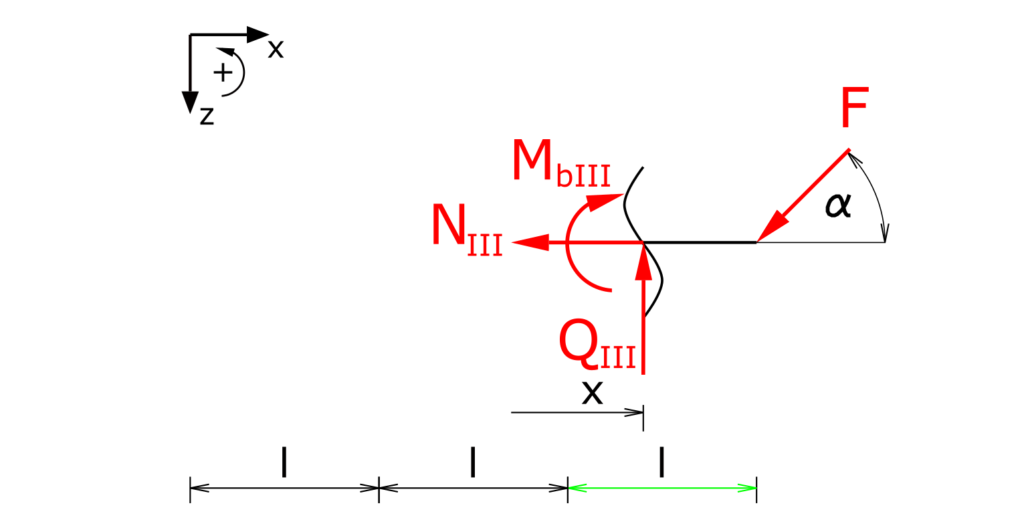
Aufstellen der Gleichgewichtsbedingungen für Kräfte in z-Richtung sowie für die Momente:
\[ \tag{22} \sum F_x = 0 = -N_{III} - F \cdot cos \alpha \]
\[ \tag{23} \sum F_z = 0 = -Q_{III} + F \cdot sin \alpha \]
\[ \tag{24} \sum M(x) = 0 = -M_{bIII} - F \cdot sin \alpha \cdot (3l-x) \]
Die Schnittgrößen in Bereich 3 ergeben sich damit zu
\[ \tag{25} N_{III} = - F \cdot cos \alpha \]
\[ \tag{26} Q_{III} = F \cdot sin \alpha \]
\[ \tag{27} M_{bIII} = - F \cdot sin \alpha \cdot (3l-x) \]
Damit sind alle Lagerreaktionen und Schnittgrößen des Trägers bestimmt.
Hier gibt es weitere interessante Aufgaben und Lösungen zur Technischen Mechanik 2 - Festigkeitslehre.
Werbung




